RFG: Test-Time Scaling for Diffusion Large Language Model Reasoning with Reward-Free Guidance (2509.25604v1)

Abstract: Diffusion LLMs (dLLMs) have shown great potential in large-scale language modeling, and there is an increasing interest in further improving the capacity to solve complex problems by guiding the reasoning process step by step. Common practice for autoregressive LLMs typically learns a process reward model with dense annotation for each intermediate step. However, this is challenging for dLLMs where the generation is in an any-order fashion and intermediate states are partially masked sentences. To this end, in this paper, we propose reward-free guidance (RFG), a principled method for guiding the reasoning trajectory of dLLMs without explicit process reward. The key idea of RFG is to parameterize the process reward by log-likelihood ratios of the enhanced and reference dLLMs, where the enhanced model can be easily obtained by any off-the-shelf dLLM that has been post-trained with reinforcement learning (RL) or supervised fine-tuning (SFT). We provide theoretical justification that RFG induces the reward-guided sampling distribution with no additional reward. We conduct comprehensive experiments on four challenging mathematical reasoning and code generation benchmarks using a diverse suite of dLLMs enhanced with various post-training methods. RFG consistently yields significant improvements across all tasks and model types, achieving accuracy gains of up to 9.2%. These findings establish RFG as a general training-free framework that scales test-time reasoning without reliance on external reward models.

• The paper presents Reward-Free Guidance (RFG) as a training-free method that scales diffusion LLM reasoning using log-likelihood ratios.
• Empirical results on benchmarks like GSM8K and HumanEval demonstrate significant accuracy gains, reaching improvements of up to 9.2%.
• RFG is model-agnostic and integrates seamlessly into existing inference pipelines with robustness to a wide range of guidance strength values.

Reward-Free Guidance for Diffusion LLMs: A Principled Test-Time Scaling Framework

Overview and Motivation

Diffusion LLMs (dLLMs) have emerged as a compelling alternative to autoregressive (AR) LLMs, offering any-order generation, reduced exposure bias, and parallelizable inference. However, while AR LLMs have benefited from test-time scaling and reward-based guidance to enhance reasoning, analogous methods for dLLMs have been limited by the lack of tractable process reward models (PRMs) due to the masked, any-order nature of their intermediate states. The paper introduces Reward-Free Guidance (RFG), a theoretically grounded, training-free framework for test-time scaling of dLLM reasoning, which leverages the log-likelihood ratio between an enhanced (policy) and a reference dLLM to guide the denoising trajectory without explicit process rewards.

RFG: Theoretical Foundations and Algorithm

RFG is motivated by the observation that, in AR LLMs, process reward models can be used to guide generation at each step, but this is infeasible for dLLMs due to the combinatorial and incomplete nature of masked intermediates. RFG circumvents this by parameterizing the reward as the log-likelihood ratio between a policy dLLM (e.g., RL- or SFT-enhanced) and a reference dLLM (e.g., base pretrained), i.e.,

$$r_\theta(\cdot) = \beta \log \frac{p_\theta(\cdot)}{p_\text{ref}(\cdot)}$$

This reward can be decomposed at each denoising step, yielding a step-wise PRM:

$$r_\theta^t(\mathbf{x}_{t-1}|\mathbf{x}_t) = \beta \log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{p_\text{ref}(\mathbf{x}_{t-1}|\mathbf{x}_t)}$$

The guided sampling distribution at each step is then:

$$\log p^*(\mathbf{x}_{t-1}|\mathbf{x}_t) = (1 + w) \log p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) - w \log p_\text{ref}(\mathbf{x}_{t-1}|\mathbf{x}_t) + C$$

where $w$ is a tunable guidance strength. This formulation is closely related to classifier-free guidance (CFG) in diffusion models, but instead of conditional/unconditional models, RFG uses policy/reference dLLMs.

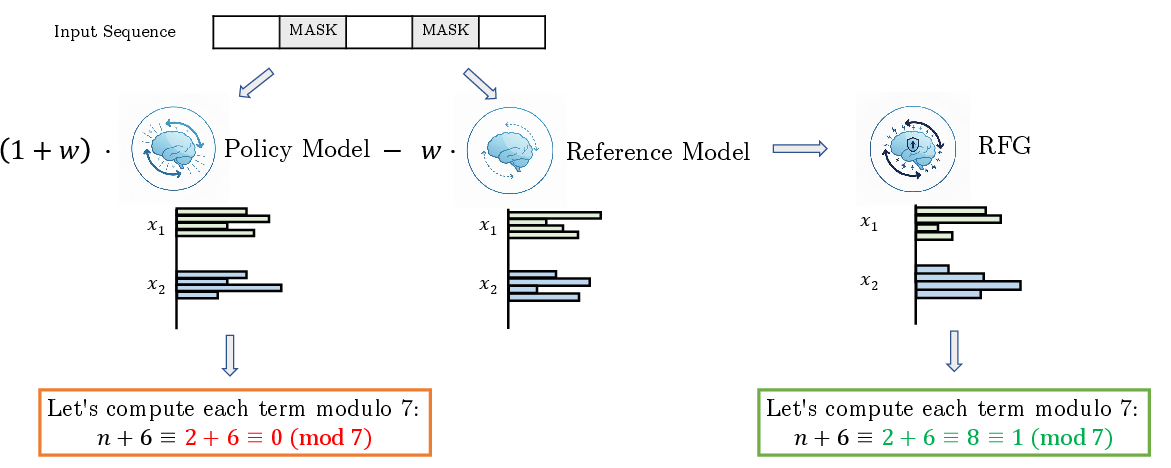
Figure 1: Sampling illustration for original policy model and RFG.

The RFG algorithm is model-agnostic and requires no additional training. At each denoising step, logits from both models are combined according to the above formula, and the next state is sampled using any standard dLLM decoding strategy (e.g., block diffusion, low-confidence remasking, nucleus sampling).

Empirical Results

RFG is evaluated on four challenging benchmarks: GSM8K and MATH-500 for mathematical reasoning, and HumanEval and MBPP for code generation. The experiments use two dLLM families (LLaDA and Dream) and both SFT- and RL-enhanced variants as policy models. RFG is compared against the original post-trained models and a naive ensemble baseline (logit averaging with identical compute).

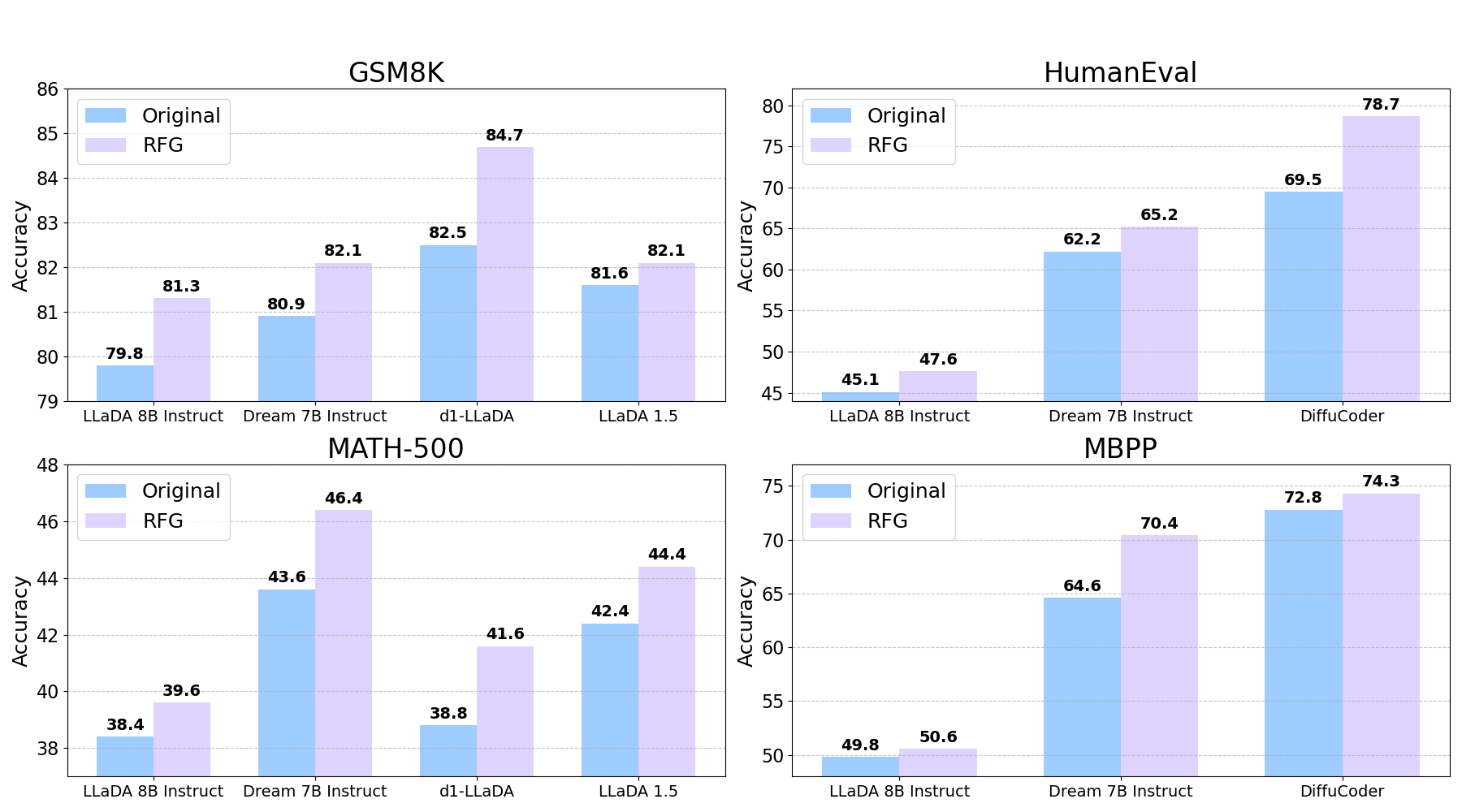
Figure 2: RFG consistently achieves significant improvements across all four tasks and various model types with different post-training methods.

Across all settings, RFG yields consistent and significant improvements over both baselines, with accuracy gains up to 9.2%. Notably, the improvements are robust to the choice of guidance strength $w$ and are not attributable to increased compute or naive ensembling, but to the principled guidance mechanism.

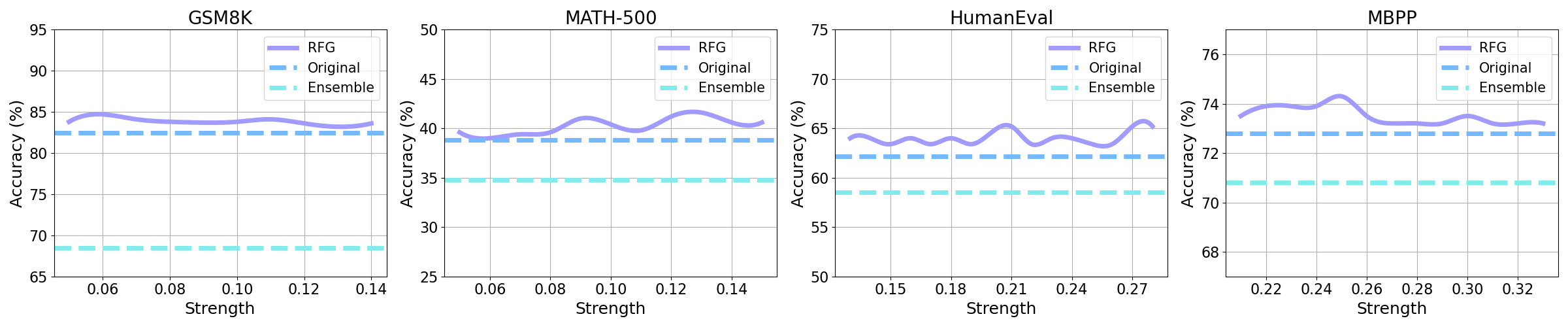
Figure 3: Accuracy of RFG under varying guidance strength $w$ across four benchmarks. RFG consistently improves performance over a broad range of $w$.

Qualitative analysis demonstrates that RFG-corrected generations exhibit more coherent multi-step reasoning, fewer hallucinations, and more robust code, as evidenced by case studies in both math and code domains.

Implementation and Practical Considerations

Implementation: RFG can be integrated into any dLLM inference pipeline with minimal modification. The only requirement is access to both a reference and an enhanced dLLM. At each denoising step, compute logits for all masked positions from both models, combine them as per the RFG formula, and sample the next state. The denoising schedule and decoding strategy are modular and can be adapted to the underlying dLLM architecture.

Resource Requirements: RFG doubles the inference-time compute relative to single-model decoding, as both models must be evaluated at each step. However, this is comparable to naive ensembling, and the empirical results show that RFG's gains are not merely due to increased compute.

Hyperparameter Sensitivity: The guidance strength $w$ is robust; strong performance is observed across a wide range of values, reducing the need for fine-tuning.

Model-Agnosticism: RFG is agnostic to the training method of the policy model. Both RL- and SFT-enhanced dLLMs can be used, and even instruction-tuned models without explicit RL yield significant gains.

Limitations: RFG requires access to both a reference and an enhanced dLLM, which may not always be feasible in resource-constrained settings. The method is currently evaluated on text-only dLLMs; extension to multimodal diffusion models is a promising direction.

Implications and Future Directions

RFG establishes a general, training-free framework for test-time scaling of dLLM reasoning, obviating the need for explicit process reward models or dense intermediate annotations. Theoretically, it connects trajectory-level reward optimization with step-wise guidance via log-likelihood ratios, and empirically, it demonstrates robust improvements across diverse tasks and model types.

Practical Implications:

• RFG enables practitioners to leverage existing enhanced dLLMs for improved reasoning at inference, without retraining or external reward models.
• The method is compatible with any dLLM architecture and can be combined with other test-time scaling or alignment techniques.

Theoretical Implications:

• RFG generalizes the concept of classifier-free guidance to the domain of reasoning and alignment in discrete diffusion models.
• The log-likelihood ratio parameterization provides a unified view of reward-guided sampling in both AR and diffusion LLMs.

Future Directions:

• Extension to multimodal diffusion models (e.g., LaViDa, MMaDA, Dimple) for vision-language reasoning.
• Integration with agentic reasoning systems and dynamic test-time compute allocation.
• Exploration of adaptive or learned guidance strength schedules.
• Application to domains requiring robust alignment without costly retraining, such as safety-critical or domain-adapted LLMs.

Conclusion

Reward-Free Guidance (RFG) provides a principled, training-free approach for test-time scaling of diffusion LLM reasoning. By leveraging the log-likelihood ratio between enhanced and reference dLLMs, RFG enables step-wise guidance without explicit process rewards, yielding consistent improvements across mathematical and code reasoning tasks. The framework is theoretically justified, empirically validated, and broadly applicable, offering a scalable alternative to retraining for alignment and reasoning enhancement in generative models.