SLA: Beyond Sparsity in Diffusion Transformers via Fine-Tunable Sparse-Linear Attention (2509.24006v1)
Abstract: In Diffusion Transformer (DiT) models, particularly for video generation, attention latency is a major bottleneck due to the long sequence length and the quadratic complexity. We find that attention weights can be separated into two parts: a small fraction of large weights with high rank and the remaining weights with very low rank. This naturally suggests applying sparse acceleration to the first part and low-rank acceleration to the second. Based on this finding, we propose SLA (Sparse-Linear Attention), a trainable attention method that fuses sparse and linear attention to accelerate diffusion models. SLA classifies attention weights into critical, marginal, and negligible categories, applying O(N2) attention to critical weights, O(N) attention to marginal weights, and skipping negligible ones. SLA combines these computations into a single GPU kernel and supports both forward and backward passes. With only a few fine-tuning steps using SLA, DiT models achieve a 20x reduction in attention computation, resulting in significant acceleration without loss of generation quality. Experiments show that SLA reduces attention computation by 95% without degrading end-to-end generation quality, outperforming baseline methods. In addition, we implement an efficient GPU kernel for SLA, which yields a 13.7x speedup in attention computation and a 2.2x end-to-end speedup in video generation on Wan2.1-1.3B.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces a new way to speed up “attention” in Diffusion Transformer (DiT) models, especially for making videos. Attention is a core part of Transformers but becomes very slow when sequences are long (like videos with many frames), because it normally checks every item against every other item. The authors propose SLA (Sparse–Linear Attention), a method that smartly combines two ideas—sparse attention and linear attention—to keep quality high while cutting the time and computation needed by attention.
Key Objectives
The paper asks a simple question: How can we make attention in video-generating Transformers much faster without hurting the quality of the videos?
To do that, the authors aim to:
- Understand the structure of attention weights (which say how much one token should “pay attention” to another).
- Use this understanding to split the attention work into parts that must be done exactly, parts that can be done faster with approximations, and parts that can be skipped.
- Build a practical GPU implementation that works in both training and inference.
- Show that this method keeps video quality while dramatically speeding up generation.
Methods and Approach
Think of attention like reading a huge textbook: in theory, you compare every sentence to every other sentence to figure out what’s important. That takes a long time. The paper breaks this problem into a simpler plan using a few key ideas.
- What is attention and why is it slow?
- Standard attention compares all pairs of tokens, which takes time that grows like the square of the sequence length (). For long videos, can be 10,000–100,000, so this is extremely slow.
- Two known shortcuts and their problems
- Sparse attention: Only compute the most important comparisons and skip the tiny ones. This helps, but in practice you still end up computing a lot—often not sparse enough for big speed-ups.
- Linear attention: Reformulate attention so its cost grows linearly (). Sounds great, but for video diffusion models, using linear attention alone usually hurts quality.
- A key observation about attention weights
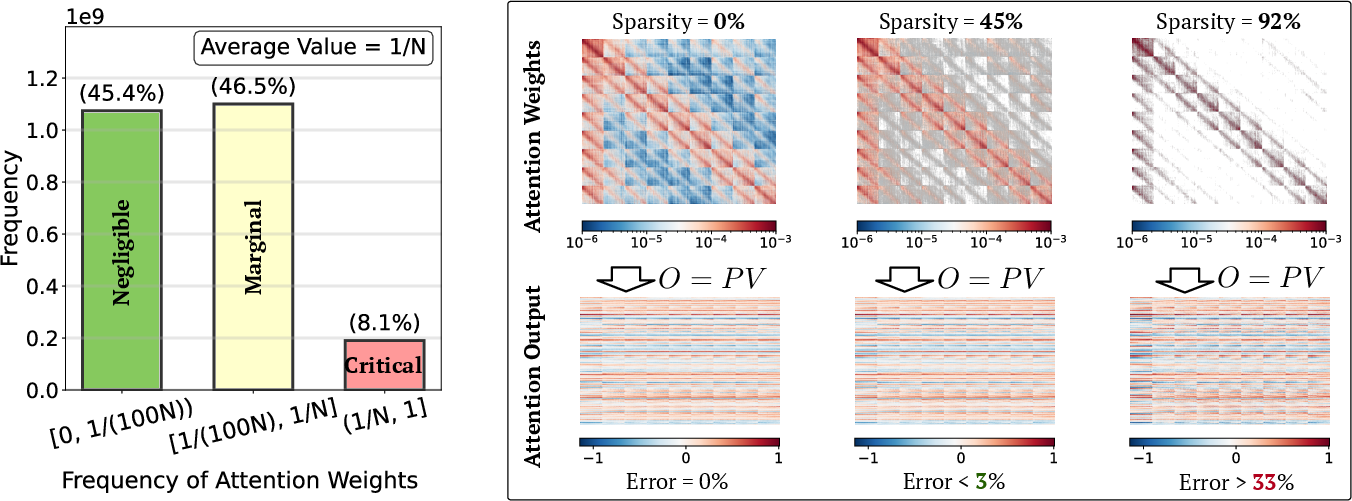
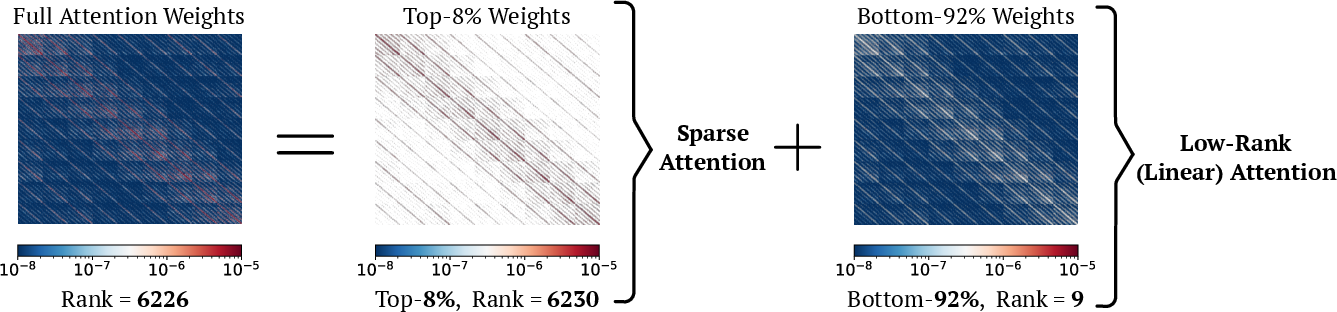
- Attention weights can be split into:
- A small set of big, important weights that are complex (high-rank) and must be computed accurately.
- A large set of small weights that are simple (low-rank) and can be handled with a faster method.
- In everyday terms: a few parts really matter and are complicated; many parts matter less and follow simple patterns.
- The SLA plan: classify attention into three types To make this work, SLA first builds a smaller “preview map” of attention (by averaging tokens into blocks). Then it labels each block as:
- Critical: the most important weights—compute them exactly with fast, optimized full attention.
- Marginal: medium-importance weights—compute them using linear attention (cheap and fast).
- Negligible: tiny weights—skip them entirely.
Because the marginal part uses linear attention and the negligible part is skipped, the overall amount of work drops drastically, while the critical part preserves accuracy where it matters most.
- Training and efficiency
- SLA is fine-tuned: you swap the old attention for SLA and train the model for a small number of steps so it adapts.
- The authors wrote a single fused GPU “kernel” that handles both sparse and linear parts together—this reduces overhead and speeds things up in both the forward and backward passes.
Analogy for “rank”: If a picture can be described with just a few simple shapes, it’s “low-rank.” If it needs lots of unique details, it’s “high-rank.” Most small attention weights look like simple, repeatable patterns (low-rank), while a few big weights need detailed, exact computation (high-rank).
Main Findings
The results are striking:
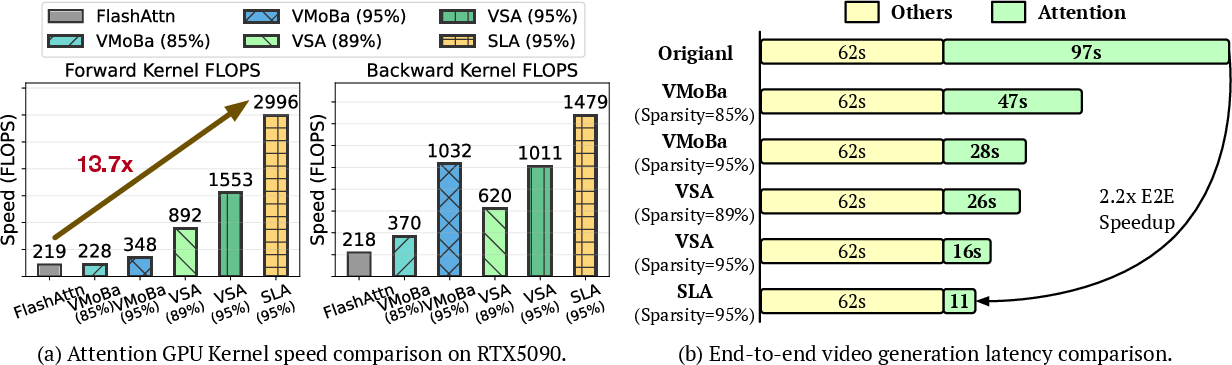
- SLA cuts attention computation by about 95% and often delivers around a 20× reduction compared to full attention.
- The attention kernel (the GPU code that does attention) runs about 13.7× faster.
- End-to-end video generation speeds up by about 2.2× on the Wan2.1-1.3B model.
- Most importantly, video quality stays essentially the same as full attention, even at very high sparsity (they skip or approximate most attention work).
- Compared to other methods that only use sparse attention or only use linear attention, SLA is both faster and produces better video quality.
In practice, they found:
- Only about 5% of blocks need exact attention (critical).
- About 10% can be safely skipped (negligible).
- The rest (marginal) are handled with linear attention, which is extremely cheap in video models (less than 0.5% of full attention cost).
- A short fine-tuning (e.g., 2,000 steps) is enough to make the model adapt and keep quality high.
Implications and Impact
This research shows a practical way to make video generation models much faster without sacrificing quality. By focusing heavy computation on the few parts that truly matter and treating the rest with simple, fast methods, SLA:
- Makes long-sequence attention more manageable.
- Reduces costs for training and inference.
- Helps deploy stronger video models on real hardware with lower latency.
- Opens the door to larger, more complex models and longer videos without huge slowdowns.
In short, SLA is a smart balance: do the hard work only where it’s necessary, and use lighter methods elsewhere. This hybrid approach could influence future designs for efficient attention in not only video diffusion models but also other long-sequence tasks.
Collections
Sign up for free to add this paper to one or more collections.