Mechanistic Independence: A Principle for Identifiable Disentangled Representations (2509.22196v1)

Abstract: Disentangled representations seek to recover latent factors of variation underlying observed data, yet their identifiability is still not fully understood. We introduce a unified framework in which disentanglement is achieved through mechanistic independence, which characterizes latent factors by how they act on observed variables rather than by their latent distribution. This perspective is invariant to changes of the latent density, even when such changes induce statistical dependencies among factors. Within this framework, we propose several related independence criteria -- ranging from support-based and sparsity-based to higher-order conditions -- and show that each yields identifiability of latent subspaces, even under nonlinear, non-invertible mixing. We further establish a hierarchy among these criteria and provide a graph-theoretic characterization of latent subspaces as connected components. Together, these results clarify the conditions under which disentangled representations can be identified without relying on statistical assumptions.

• The paper establishes a novel framework using mechanistic independence to achieve identifiable disentangled representations even with nonlinear, non-invertible mixing.
• It introduces specific independence criteria (Types D, M, and S) and defines conditions that transition local disentanglement to a global framework.
• The study employs graph-theoretic visualization to illustrate structural independence across latent subspaces, providing practical guidelines for improved representation learning.

Mechanistic Independence: A Principle for Identifiable Disentangled Representations

This research introduces a framework for achieving disentangled representations through mechanistic independence, focusing on identifiability even under nonlinear, non-invertible mixing conditions. The authors propose independence criteria and establish the conditions under which disentangled representations can be identified.

Introduction

The paper addresses the challenge of achieving identifiable disentangled representations, which capture the underlying latent factors of variation within observed data. Traditional approaches often rely on statistical independence, which may not suffice for nonlinear mixing scenarios. The authors propose a shift towards defining latent factors through their action on observable variables, independent of latent density distributions.

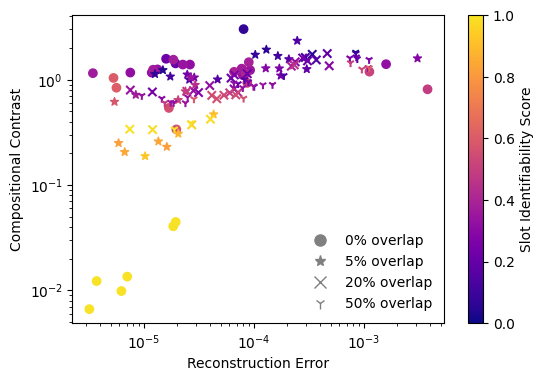
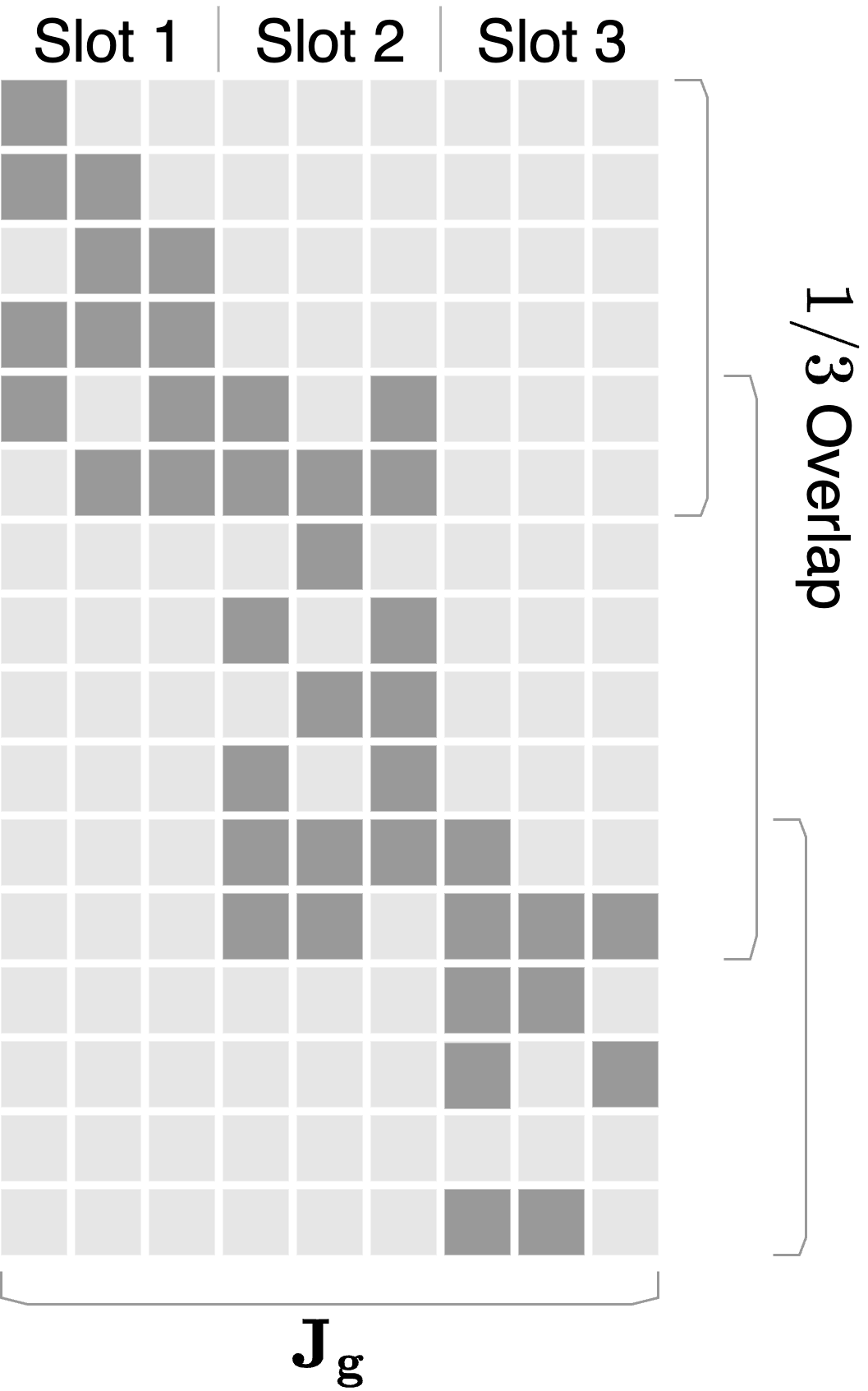
Figure 1: Experimental setup reference illustrating distinct factor spaces and non-overlapping influences on observations.

Disentanglement and Identifiability

Data Generating Process

Latent factors of variation are modeled as subspaces of a product manifold. The generator maps latent configurations to an observation manifold, aligning with the manifold hypothesis in representation learning.

Disentangled Representations

A representation is described as disentangled if each component is influenced by a single latent factor or a restricted subset of them. This is defined using decomposable maps, emphasizing independence through mechanistic terms rather than statistical ones.

Identifiability

The paper establishes that local disentanglement under certain topological assumptions, such as path-connectedness, can lead to global disentanglement. The criteria involve locally injective maps and path-connectedness of slices in source space, which propagate disentangled structure globally.

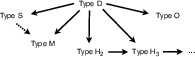
Figure 2: Graph-theoretic representation showing implications among different independence types, highlighting logical implications across types.

Identifiability via Independent Mechanisms

The focus is on understanding disentanglement at the level of generative mechanisms. Various independence criteria—Type D, M, S, and H—are explored, each leading to conditions supporting disentangled representations.

Local Identifiability of Type D

Type D independence involves factors influencing disjoint observation coordinates. This structural independence ensures identifiability by constraining factor interactions to exclusive coordinates.

Local Identifiability of Type M and S

Type M relaxes the disjointness to allow for limited overlap, using mutual non-inclusion. Meanwhile, Type S introduces a sparsity gap, focusing on column sparsity in Jacobians under aligned product bases, enforcing identifiability through hierarchical topological structures.

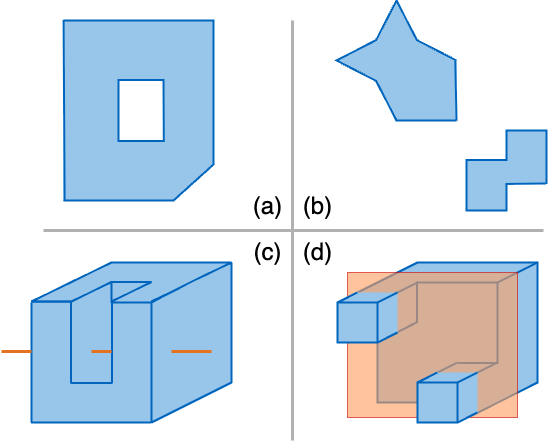
Figure 3: Examples demonstrating diverse connectedness and independence within slices, illustrating complex interactions.

Discussion

Hierarchy of Independence

Various independence criteria create a hierarchical framework, where conditions such as Type D imply stronger conditions of independence than others. These relations illustrate trade-offs in achievable identifiability based on the strength of imposed independence.

Connected Graph Components for Factorization

Mechanistic independence can be visualized using graph structures, translating the factorization problem into characterizing connected components within graphs. This graphical approach highlights the structural independence across latent subspaces.

Conclusion

The proposed framework provides significant insights into disentangled representation learning without relying heavily on statistical assumptions. By formulating independence mechanisms at the generator's level, the paper aids in establishing clear criteria and guidelines for achieving disentangled representations. This work lays the foundation for further exploration into integrating mechanistic and statistical assumptions for improved model identifiability.