When Does Reasoning Matter? A Controlled Study of Reasoning's Contribution to Model Performance (2509.22193v1)
Abstract: LLMs with reasoning capabilities have achieved state-of-the-art performance on a wide range of tasks. Despite its empirical success, the tasks and model scales at which reasoning becomes effective, as well as its training and inference costs, remain underexplored. In this work, we rely on a synthetic data distillation framework to conduct a large-scale supervised study. We compare Instruction Fine-Tuning (IFT) and reasoning models of varying sizes, on a wide range of math-centric and general-purpose tasks, evaluating both multiple-choice and open-ended formats. Our analysis reveals that reasoning consistently improves model performance, often matching or surpassing significantly larger IFT systems. Notably, while IFT remains Pareto-optimal in training and inference costs, reasoning models become increasingly valuable as model size scales, overcoming IFT performance limits on reasoning-intensive and open-ended tasks.
Summary
- The paper presents a controlled study that isolates reasoning supervision effects, demonstrating that explicit reasoning improves performance on complex tasks as model size increases.
- It employs synthetic data distillation and paired training outputs to compare reasoning-style outputs with IFT, revealing that moderate reasoning ratios offer optimal accuracy-cost trade-offs.
- The findings imply that hybrid training and domain-specific adaptation benefit larger models, suggesting a practical strategy to combine concise IFT with enriched reasoning for complex problem solving.
Controlled Analysis of Reasoning's Contribution to LLM Performance
Introduction and Motivation
This paper presents a rigorous, large-scale controlled paper to disentangle the contribution of explicit reasoning supervision in LLMs, contrasting it with standard Instruction Fine-Tuning (IFT). The authors leverage a synthetic data distillation framework, generating paired IFT and reasoning-style outputs from a single teacher model for identical prompts, enabling direct attribution of performance differences to supervision format. The paper spans five student model sizes (0.5B–14B parameters), two data domains (general-purpose and math-centric), and both multiple-choice (MC) and open-ended (OE) evaluation formats, with over 1.6M training pairs and 70k H100 GPU-hours.
The central questions addressed are: (1) Which tasks and model scales benefit most from reasoning supervision? (2) How do these gains trade off against training and inference costs? (3) What actionable guidance can be provided for practitioners regarding the deployment of reasoning-centric models?
Experimental Design
The distillation protocol employs Qwen3-235B-A22B as the teacher, with Qwen2.5 base students. For each input question, both IFT and reasoning-style answers are generated, controlling for data domain and supervision format. Training is performed exclusively on synthetic data, with no RL or human feedback, and the fraction of reasoning instances () is systematically varied. Evaluation is conducted on 12 benchmarks, using Llama-3 Nemotron Ultra as an LLM-based judge to ensure consistent scoring.
Main Results: Task Sensitivity and Scaling Dynamics
The paper finds that reasoning supervision yields substantial and consistent gains on open-ended and math-centric tasks, especially as model size increases. For example, 3B-parameter students trained with reasoning match or surpass the performance of 14B IFT models on math OE and MC tasks, demonstrating that reasoning can compensate for reduced model capacity.
Figure 1: Downstream performance of mono-phasic models. Reasoning-trained students outperform IFT counterparts on reasoning-intensive tasks, especially at larger scales.
However, for general-purpose multiple-choice tasks, reasoning provides limited or inconsistent improvements, and IFT remains competitive for models under 1.5B parameters. This highlights a strong task dependency: reasoning traces are most valuable for multi-step problem solving, while factual or classification tasks do not benefit as much.
Mixing IFT and Reasoning: Sequential vs. Mixed Training
The authors investigate both sequential (IFT followed by reasoning) and mixed (joint) training regimes. Mixed training with moderate reasoning ratios (25–50%) can outperform pure IFT on math tasks while maintaining concise outputs, but exhibits instability and abrupt transitions in output style as the reasoning ratio increases.
Figure 2: Comparison of sequential and mixed training scenarios across reasoning ratios. Mixed training can yield synergies but is unstable; sequential training shows no accuracy gains from combining IFT and reasoning.
Sequential training does not yield accuracy improvements over pure reasoning or IFT, except for the smallest models on general MC tasks. For open-ended tasks, accuracy continues to rise with higher reasoning ratios, while MC tasks plateau, indicating that the benefit of reasoning is concentrated in tasks requiring complex solution paths.
Figure 3: Impact of reasoning ratio on downstream performance. Open-ended tasks show monotonic accuracy gains with increased reasoning supervision; MC tasks plateau.
Domain-Specific Adaptation
Bi-phasic adaptation (general followed by math-centric training) is effective only for models above 1.5B parameters. Math-specialized reasoning models achieve strong in-domain performance and retain general capabilities at scales above 3B, while smaller models suffer from catastrophic forgetting when adapted to math.
Figure 4: Downstream performance of models trained sequentially on general and math-centric data. Math adaptation benefits larger models; smaller models may forget general capabilities.
Accuracy-Efficiency Trade-Offs
The paper provides a detailed analysis of training and inference FLOPs. IFT models are consistently Pareto-optimal in both training and inference cost, with performance scaling reliably with model size. Reasoning models reach Pareto optimality only at larger scales and intermediate reasoning ratios (25–75%) offer the best trade-offs, never being outperformed by pure reasoning or IFT.
Figure 5: Accuracy versus training FLOPs. IFT models are Pareto-optimal; intermediate reasoning ratios offer efficient accuracy gains.
At inference, reasoning outputs are longer and more expensive, with open-ended tasks incurring a 7× cost increase and MC tasks 10–15× when switching from IFT to reasoning. However, longer generations are correlated with higher error rates, and simple early-stopping strategies reduce cost but also degrade accuracy, failing to shift the Pareto frontier.
Figure 6: Accuracy versus inference FLOPs. IFT remains Pareto-optimal; reasoning approaches optimality at larger scales.
Figure 7: Answer length analysis. Incorrect reasoning outputs tend to be longer, suggesting inefficiency in generation.
Additional Insights and Scaling Trends
Increasing the maximum generation length benefits certain math tasks, indicating that some problems require extended reasoning traces. Reasoning models extrapolate well beyond training lengths, suggesting robustness in generation. Inference FLOPs scale log-linearly with model size, with reasoning models incurring higher costs for MC tasks but similar scaling for OE and math tasks.
Implications and Future Directions
The findings have direct implications for LLM deployment:
- Reasoning supervision is essential for breaking performance plateaus on reasoning-intensive and open-ended tasks, especially above the 7B-parameter scale.
- IFT remains the cost-efficient baseline for factual and classification tasks, and for smaller models.
- Hybrid training regimes with moderate reasoning ratios offer the best accuracy-efficiency trade-offs.
- Domain-specific adaptation is only beneficial for sufficiently large models; smaller models risk catastrophic forgetting.
The controlled distillation framework enables reproducible, confounder-free analysis and is extensible to other domains (e.g., code, law, multilingual tasks), alternative optimization techniques (RL, preference-based, logit distillation), and larger model scales.
Conclusion
This paper provides a comprehensive, controlled characterization of when and why reasoning supervision matters in LLMs. Reasoning signals are not redundant but complementary, growing in value with model scale and task complexity. The results inform both theoretical understanding and practical deployment, suggesting that future LLM development should focus on hybrid approaches that combine the conciseness of IFT with the depth of reasoning, tailored to task and scale. The open release of code and data further facilitates ongoing research in this area.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper asks a simple question: when does “reasoning” actually help LLMs do better? Reasoning here means the model explains its steps (like “showing your work” in math) instead of just giving short answers. The authors compare two training styles:
- Instruction Fine-Tuning (IFT): teaches models to give concise answers.
- Reasoning: teaches models to write out their thinking step by step.
They test both styles across many tasks, different model sizes, and measure not just accuracy but also how much computer power it costs to train and use these models.
What questions did the researchers ask?
The paper focuses on three clear questions:
- Which kinds of tasks benefit most from reasoning?
- How does a model’s size change the value of reasoning?
- Is the extra cost (longer training and longer answers) worth it compared to standard IFT?
How did they paper it?
The basic idea: a teacher and several students
Think of one big “teacher” model and several smaller “student” models. The teacher is asked the same questions twice:
- Once with reasoning turned off (short IFT-style answer).
- Once with reasoning turned on (step-by-step explanation).
These paired answers (short vs. step-by-step for the same question) become the training data for the student models. This way, the only thing that changes is the style of supervision, not the question or the teacher’s knowledge.
Training styles: IFT vs. Reasoning, and mixing them
The students (ranging from tiny to medium-large) are trained in different ways:
- Pure IFT: only short answers.
- Pure Reasoning: only step-by-step answers.
- Mixed: a chosen percentage of reasoning examples mixed with IFT, either blended together from the start or done in two stages (first IFT, then reasoning).
Reasoning answers are longer (more tokens), so they cost more to train and use. The authors measure that cost carefully.
Tasks they tested
They evaluate 12 benchmarks across two formats:
- Multiple-choice (MC): pick from given options.
- Open-ended (OE): write an answer freely.
They cover:
- General tasks (like common sense and reading comprehension).
- Math tasks (like solving math word problems or contest questions).
Open-ended math tasks are the most “reasoning-heavy,” because you really need to show steps.
Measuring results and costs
They look at:
- Accuracy: how often the model gets it right.
- Training cost: how much compute it takes to train under different styles.
- Inference cost: how much compute it takes to produce answers (longer reasoning answers cost more).
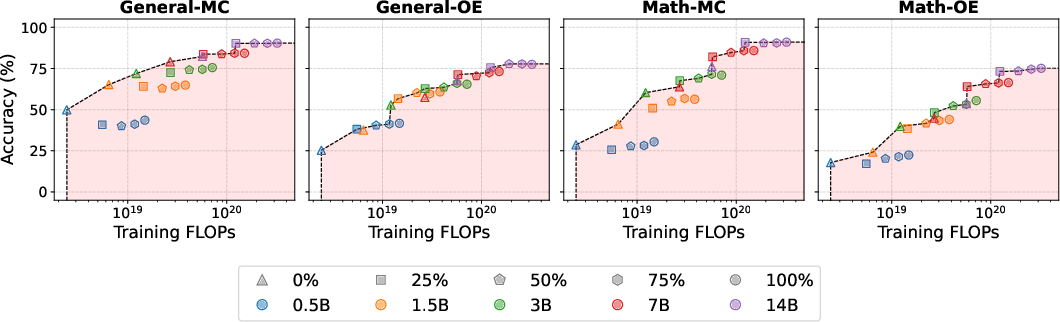
- “Pareto-optimality”: a setup is Pareto-optimal when you can’t get higher accuracy without paying more cost, and you can’t lower cost without losing accuracy. It’s the best balance.
They also check answer length and notice that very long generations tend to be wrong more often.
What did they find?
Here are the main takeaways from the experiments:
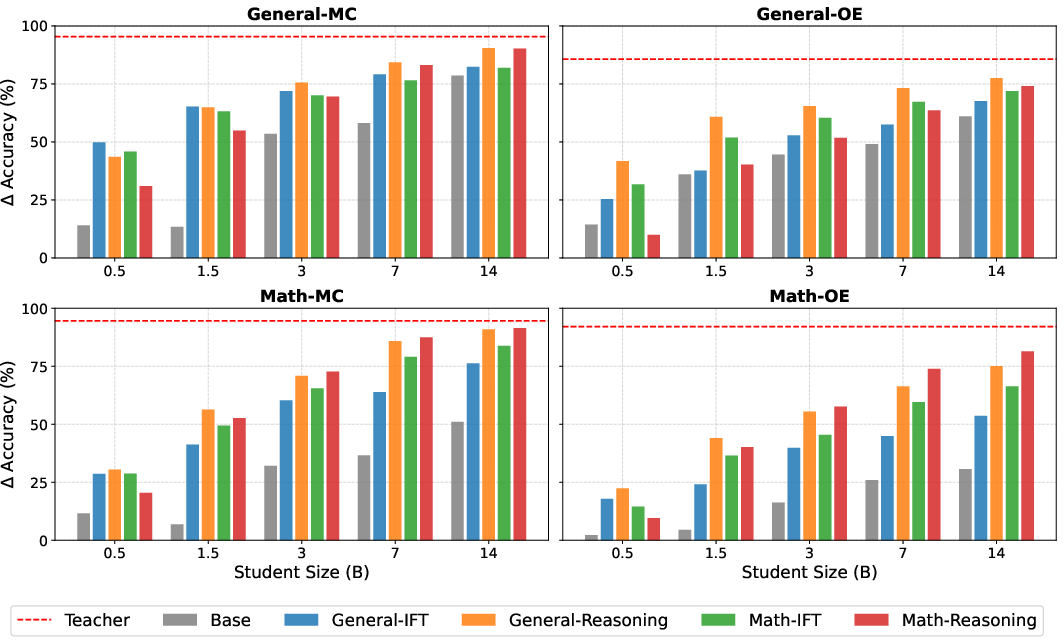
- Reasoning helps most on open-ended and math tasks. For multiple-choice on general topics, the gains are small or inconsistent.
- As models get larger, reasoning matters more. A 3B-parameter student trained with reasoning can match or nearly match a 14B-parameter student trained with IFT on reasoning-heavy tasks.
- For small models on simple tasks, IFT is still very competitive. Small models often struggle to use reasoning traces well on non-reasoning tasks.
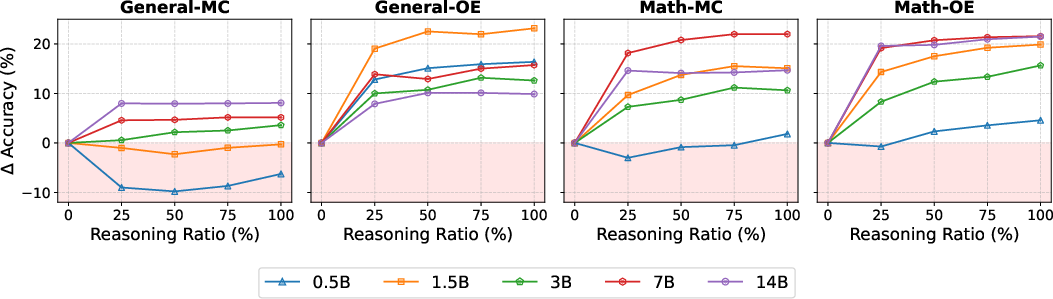
- Mixing IFT and reasoning can help a bit for math if you keep reasoning to roughly 25–50% of training, but it’s unstable. Doing IFT first and reasoning later (sequential) usually doesn’t boost accuracy compared to just training with reasoning.
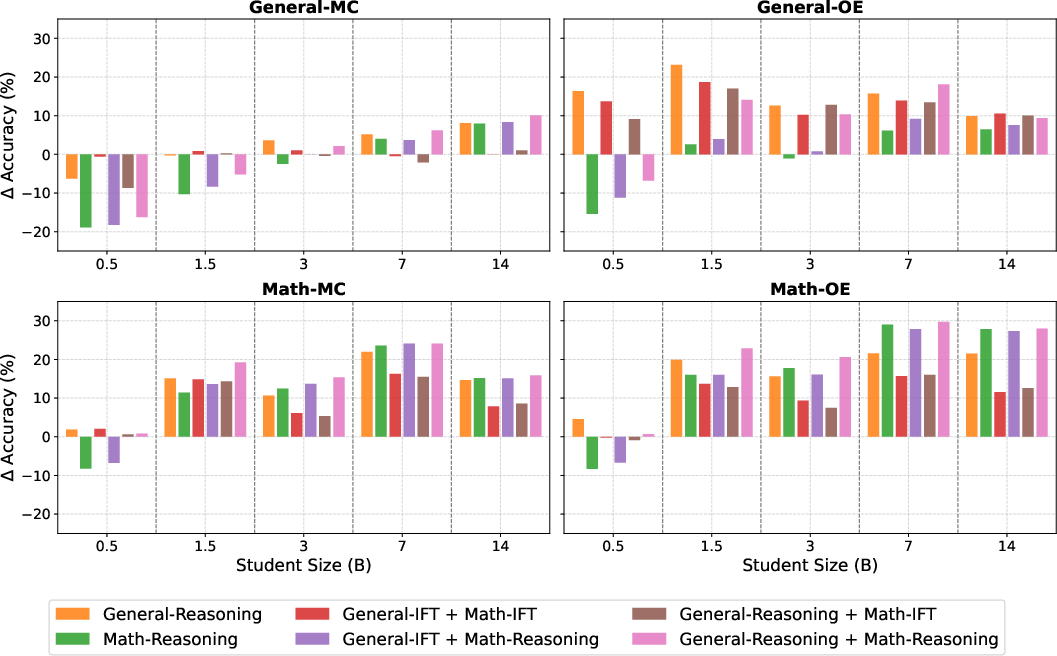
- Specializing on math improves results mainly for bigger models (around 1.5B and up). Very small models can “forget” general skills if you push them too hard into a niche.
- Cost trade-offs matter. IFT is generally the best cost-effective choice for both training and inference. Reasoning becomes cost-effective as you scale up, especially for open-ended tasks. Using a moderate amount of reasoning data often hits a sweet spot: better accuracy without huge costs.
- Longer answers often mean lower accuracy. Cutting off generation early saves compute but also drops accuracy and moves you away from the best accuracy–cost balance.
Why it matters
This paper provides practical guidance:
- If your tasks are simple or multiple-choice, and your model is small, stick with IFT. It’s cheaper and already good.
- If your tasks need step-by-step thinking (like math or harder open-ended problems), and your model is medium to large, reasoning training can break through performance limits that IFT alone can’t.
- If you care about costs, moderate amounts of reasoning in training can give solid gains without too much extra compute.
- For domain specialization (like math), bigger models benefit most, while very small ones may lose general skills.
The authors also release their code and datasets, making it easier for others to repeat and extend this kind of controlled comparison. Overall, the message is: reasoning isn’t magic everywhere—it shines most on tasks that truly require thinking, and its value grows as your models get larger.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, actionable list of what remains missing, uncertain, or unexplored in the paper.
- Confounding teacher-generation settings: reasoning and IFT traces were produced with different sampling parameters (τ/p), leaving open whether observed gains stem partly from decoding choices rather than supervision format; run ablations with identical generation settings for both modes.
- Single-teacher dependency: all supervision comes from Qwen3-235B-A22B with an internal “reasoning flag”; assess robustness across multiple teachers (architectures, sizes, MoE vs. dense) and verify the semantics of “reasoning mode” are comparable across teachers.
- Synthetic-only supervision: students are trained exclusively on teacher-generated data; validate conclusions with human-authored labels/rationales and hybrid datasets to check external validity and reduce teacher-style artifacts.
- Evaluation-by-LLM bias: a single judge (Nemotron Ultra 253B) scores all tasks; quantify judge reliability via human adjudication, cross-judge consensus, and task-specific programmatic metrics (e.g., EM/F1 for SQuAD, exact option parsing for MC).
- Shot-setting asymmetry: base models are evaluated with three-shot prompts while distilled models are zero-shot; re-run with matched shot conditions to rule out confounding from prompt priming.
- Limited task coverage: coding, tool-augmented reasoning (calculator/solver), planning, theorem proving, and code execution tasks are not included; extend the testbed to these reasoning-heavy domains.
- Scale ceiling: results stop at 14B parameters; empirically test whether reasoning becomes Pareto-optimal beyond 14B and where IFT plateaus relative to larger sizes (e.g., 30B–70B).
- Mixed training instability: mixing IFT and reasoning shows high variance and abrupt “mode switching”; investigate stabilizing curricula (ratio annealing, temperature schedules), per-sample mixture selection, and token-level loss weighting.
- Domain adaptation beyond math: only math-centric adaptation is analyzed; replicate bi-phasic adaptation in other domains (biomedical, law, multilingual translation, safety) to generalize findings.
- Catastrophic forgetting in small models: 0.5B–1.5B students show degradation under domain-specific adaptation; evaluate mitigation strategies (adapters/LoRA, EWC/LwF, replay buffers, sparse finetuning).
- Reasoning-length inefficiency: longer generations are more error-prone; develop and test methods to compress or prune traces (hidden CoT, plan-then-solve, rationale distillation, scratchpad dropout, step selection).
- Budgeted decoding baseline: only a hard token cutoff was tested and hurt accuracy; compare smarter budget policies (early-exit confidence, verifier-guided stopping, dynamic reasoning gating per query).
- Step-level correctness: the quality and correctness of intermediate reasoning steps are not evaluated; add step-verification, error taxonomy, and training objectives that penalize incorrect steps.
- Loss design: the training objective treats all tokens equally; paper differential weighting of rationale vs. final answer tokens, and contrastive objectives that favor concise, correct final answers.
- Decoding policy at inference: fixed τ=1.0, p=1.0 was used; run decode ablations (greedy/top-k/top-p variations, temperature sweeps, beam search) to quantify sensitivity and efficiency impacts.
- Test-time strategies: no self-consistency, majority vote, or tree-of-thought sampling was evaluated; measure accuracy–FLOPs trade-offs of these strategies across tasks and sizes.
- Per-query reasoning gating: reasoning is either always on or off by training ratio; explore learned policies that decide whether to reason per query (benefit/cost predictor, uncertainty-aware gating).
- MC-task parsing: MC results may be influenced by judge interpretation of free-form outputs; enforce strict final-option extraction and exact matching to reduce evaluation noise.
- FLOPs-only efficiency accounting: training/inference costs are reported in FLOPs; include wall-clock latency, memory/KV-cache footprint, energy, and batch-size effects to guide deployment decisions.
- Architecture generality: students are all Qwen2.5 dense models; test other families (Llama, Mistral, Phi, Gemma), MoE vs. dense students, and decoder-only vs. hybrid architectures.
- Data contamination and overlap: potential overlap between synthetic training data and evaluation benchmarks is not audited; run contamination checks and re-evaluate on held-out, unseen test sets.
- Teacher diversity in traces: only one reasoning style is distilled; compare multiple teacher-rationale styles (concise vs. verbose, symbolic vs. natural language, code-first vs. math-first) and their impact on students.
- Safety and robustness: harmful content amplification, adversarial prompts, and robustness to distribution shift are not assessed; add safety/robustness audits for both IFT and reasoning models.
- Multilingual coverage: experiments appear English-centric; extend to multiple languages to test if reasoning benefits and costs transfer cross-lingually.
- Mechanistic insights: the paper is performance-centric; analyze representational/mechanistic changes (attention patterns, depth-of-thought proxies, calibration) induced by reasoning supervision.
- Statistical significance and replicability: variance is noted but statistical tests, multiple seeds, and CI reporting are missing; include multi-seed runs, significance testing, and reproducibility checks.
Practical Applications
Immediate Applications
The following applications can be deployed now by leveraging the paper’s findings, datasets, and code to improve accuracy-cost trade-offs and guide training/deployment choices.
- Cost-aware model selection and routing policies
- What to do: Route tasks to IFT or reasoning models based on task type and model size. Prefer IFT for multiple-choice and simpler factual/classification tasks, and enable reasoning for open-ended, math, and coding tasks, especially above ~7B parameters.
- Sectors: Software (assistants, search), Education (tutoring), Finance (analyst summaries), Customer support (knowledge-intensive cases).
- Tools/workflows: Inference gateway that tags requests as MC vs OE, complexity heuristics, and routes to (a) IFT model, (b) reasoning model, or (c) bigger IFT model as baseline.
- Assumptions/dependencies: Access to both IFT and reasoning checkpoints; reliable task-type classifier; latency budgets that tolerate longer traces for OE tasks.
- Capacity planning and TCO estimates for LLM deployment
- What to do: Use empirically grounded multipliers to forecast inference cost inflation when turning on reasoning (≈7× for OE tasks; ≈10–15× for MC tasks) and plan GPU capacity, latency SLAs, and costs accordingly.
- Sectors: All sectors operating LLMs at scale.
- Tools/workflows: Cost dashboards that model token budgets vs. accuracy, scenario planning for enabling/pausing reasoning by product surface.
- Assumptions/dependencies: Token accounting fidelity; traffic mix stability; acceptance of higher latency for complex tasks.
- Training playbook for builders: when to scale size vs. add reasoning
- What to do:
- Start with an IFT baseline; scale model size first (IFT is Pareto-optimal in training and inference cost).
- Add reasoning supervision to break plateaus, especially for open-ended and math tasks; above ~7B, expect clearer gains.
- Use intermediate reasoning ratios (25–75%) to reach Pareto-optimal trade-offs; avoid 100% reasoning unless accuracy is paramount and cost is secondary.
- Sectors: Model providers, internal ML platforms, research labs.
- Tools/workflows: Training orchestration that supports reasoning ratios; curriculum schedulers; monitoring of answer length vs. accuracy during training.
- Assumptions/dependencies: Availability of compute; stability of mixed training at chosen ratios; adherence to dataset licenses.
- Domain-specific adaptation guidance (math exemplar)
- What to do: For math-heavy products, adapt a general-reasoning model on math data if the student is ≥1.5B; expect best gains ≥3B while preserving generality. Avoid IFT-after-reasoning adaptation (no benefit observed).
- Sectors: Education (STEM tutoring), Coding (algorithmic tasks), Finance (quant modeling), Engineering (planning/scheduling).
- Tools/workflows: Two-phase fine-tuning pipelines (general → math reasoning), evaluation on Math-OE and Math-MC.
- Assumptions/dependencies: Sufficient capacity to prevent catastrophic forgetting in ≤1.5B students; representative in-domain datasets.
- Open-source controlled distillation pipeline applied to proprietary corpora
- What to do: Use the released code and paired IFT/reasoning datasets as templates to synthesize paired traces (IFT and CoT) with a single teacher on your internal data; train students for your domain.
- Sectors: Healthcare (clinical QA on internal notes), Legal (case analysis), Finance (policy/memo drafting), Enterprise search.
- Tools/workflows: Teacher-driven synthetic data generation with a reasoning flag; student fine-tuning with variable reasoning ratios.
- Assumptions/dependencies: Data governance approvals; teacher access and licensing; privacy-preserving generation.
- Evaluation SOPs that reflect reasoning sensitivity
- What to do: Evaluate models separately on MC vs. OE tasks; use LLM-as-a-judge to robustly score unstructured outputs; measure accuracy vs. FLOPs (training and inference) to inform Pareto decisions.
- Sectors: Procurement, vendor evaluation, academic benchmarking.
- Tools/workflows: Standardized evaluation harness; judge prompts; accuracy-FLOPs Pareto plots; task portfolios mirroring production.
- Assumptions/dependencies: Judge reliability and bias monitoring; reproducible decoding settings; calibration with human spot checks.
- Answer-length monitoring and guardrails
- What to do: Track length as a risk signal (longer reasoning often correlates with errors); flag very long chains for secondary verification, rerouting, or truncation warnings to users.
- Sectors: High-stakes domains (Healthcare, Legal, Finance), Developer tools (code generation review).
- Tools/workflows: Telemetry on token lengths; thresholds to trigger verifier models or human review; length-aware user feedback.
- Assumptions/dependencies: Tuning thresholds per domain; avoiding excessive false positives; verifying that truncation does not degrade safety.
- Product-level “reasoning toggle” and progressive disclosure
- What to do: Offer a user-facing toggle for “explain your work” on complex problems; default to concise IFT responses for simple queries to save cost and latency.
- Sectors: Education (step-by-step tutoring), Productivity suites (analysis write-ups), Developer tools (annotated code reasoning).
- Tools/workflows: UX controls, policy gradients per app surface (always-on reasoning in math worksheets; off by default in quick Q&A).
- Assumptions/dependencies: User comprehension of explanations; cost transparency; accessibility constraints.
- Edge vs. cloud deployment policy
- What to do: Run small IFT models on-device for routine tasks; escalate complex, open-ended tasks to cloud-based larger reasoning models.
- Sectors: Mobile assistants, field operations, embedded systems.
- Tools/workflows: On-device classifiers; elastic cloud scaling; privacy-preserving routing.
- Assumptions/dependencies: Network availability; privacy/PII constraints; clear escalation heuristics.
- Procurement and policy guidance tying accuracy to environmental cost
- What to do: Include compute and carbon disclosures in RFPs; require reporting of accuracy per inference FLOP and typical token inflation from reasoning for the task mix.
- Sectors: Government, NGOs, regulated industries.
- Tools/workflows: Standard evaluation clauses; sustainability scorecards; caps on reasoning usage for low-value tasks.
- Assumptions/dependencies: Vendor transparency; standardized FLOPs accounting; alignment with organizational ESG policies.
Long-Term Applications
These applications require further research, scaling, or engineering to stabilize training behaviors, reduce token overhead, and broaden domain coverage.
- Stable mixed-format training and curricula
- What: Methods to realize the observed synergies at 25–50% reasoning ratios without instability, preserving conciseness while gaining reasoning accuracy.
- Sectors: Model providers, academia.
- Tools/workflows: Curriculum learning, style-regularization losses, contrastive objectives to prevent abrupt “reasoning mode” shifts.
- Assumptions/dependencies: New objectives and schedulers; broader ablations across domains beyond math.
- Adaptive CoT controllers and token-budget policies
- What: Learned controllers to decide when to trigger reasoning, how long to reason, and when to stop, optimizing accuracy vs. FLOPs dynamically per query.
- Sectors: All LLM platforms; cost-sensitive SaaS.
- Tools/workflows: Bandit/RL-based controllers; uncertainty/complexity estimators; answer-length priors; verifier feedback loops.
- Assumptions/dependencies: Reliable complexity signals; safe exploration in production; guardrails to avoid accuracy collapse.
- Token-efficient reasoning compression
- What: Distillation of shorter, high-yield reasoning traces that maintain accuracy, reducing the 7–15× cost multipliers.
- Sectors: Mobile/edge, high-throughput APIs.
- Tools/workflows: Rationale compression objectives, sparse/extractive CoT, structure-aware decoding, caching reusable sub-reasoning.
- Assumptions/dependencies: Robustness of compressed explanations; domain-specific compression strategies.
- Length-aware decoding that preserves correctness
- What: Decoding algorithms that penalize unproductive chain length without harming accuracy (unlike naive truncation which the paper shows degrades performance).
- Sectors: Cloud inference providers, safety-critical apps.
- Tools/workflows: Dual-head models (reasoning + verifier), early-consensus stopping, anti-loop detectors.
- Assumptions/dependencies: Access to verifier or self-consistency signals; careful calibration per task family.
- Catastrophic-forgetting-resistant domain adaptation
- What: Methods that let ≤1.5B models specialize (e.g., math) without losing general skills; parameter-efficient modules and multi-domain rehearsal.
- Sectors: Verticalized assistants (biomed, legal, finance).
- Tools/workflows: Adapters/LoRA with rehearsal buffers, orthogonal gradient methods, domain routers.
- Assumptions/dependencies: Curated in-domain corpora; continual learning evaluation standards.
- Reasoning-aware orchestration and hardware scheduling
- What: Inference schedulers that anticipate token inflation and provision accelerators accordingly; preemption/resume for long chains; carbon-aware scheduling.
- Sectors: Cloud providers, MLOps platforms, sustainability-focused operations.
- Tools/workflows: Token-forecasting services; carbon-intensity-aware schedulers; SLAs per reasoning mode.
- Assumptions/dependencies: Accurate token forecasts; integration with cluster schedulers; carbon data availability.
- Sector-specific “explainable-by-design” systems
- What: Auditable reasoning traces for clinical decision support, legal argumentation, and financial risk memos with verifiers and citations.
- Sectors: Healthcare, Legal, Finance, Public policy.
- Tools/workflows: Reasoning + retrieval + verifier pipelines; audit logs; human-in-the-loop review.
- Assumptions/dependencies: Regulatory approvals; medical/legal validation; robust calibration to reduce overlong, error-prone chains.
- Standardization of reasoning sensitivity benchmarks and compute reporting
- What: Community standards to report accuracy vs. training/inference FLOPs and task sensitivity (MC vs. OE) for procurement and research comparability.
- Sectors: Academia, standards bodies, government.
- Tools/workflows: Shared leaderboards with Pareto frontiers; dataset cards with reasoning-sensitivity tags.
- Assumptions/dependencies: Broad adoption; consensus on FLOPs accounting.
- Integrating RL to refine reasoning with transparent attribution
- What: Combine supervised distillation (clean attribution) with efficient RL phases to refine strategies while keeping costs in check.
- Sectors: Model developers, research labs.
- Tools/workflows: Outcome-based rewards with compute caps, verifier-guided RL, off-policy reuse of synthetic traces.
- Assumptions/dependencies: Clear reporting of data/compute; safeguards against reward hacking.
- Scaling studies beyond 14B and cross-domain generalization
- What: Verify where reasoning becomes fully Pareto-optimal at inference, establish scaling laws for reasoning vs. IFT across domains (biomed, law, robotics planning).
- Sectors: Frontier labs, domain-specific model builders.
- Tools/workflows: Larger student families, multi-domain paired distillation datasets, cross-task generalization audits.
- Assumptions/dependencies: Access to larger compute; representative, licensed datasets.
Notes on Dependencies and Assumptions
- Teacher availability with a controllable reasoning flag (as in Qwen3-235B-A22B) is assumed for generating paired IFT/CoT traces; licensing and privacy constraints apply.
- Reported gains are strongest for math and open-ended tasks; benefits may vary in other domains until validated with domain-specific datasets.
- LLM-as-a-judge improves evaluation practicality but requires bias monitoring and periodic human calibration.
- The paper’s scale ceiling (14B students) suggests further validation at larger scales to finalize Pareto boundaries.
- Longer reasoning often correlates with errors; interventions must balance cost savings with accuracy and safety.
Glossary
- Abstention mechanism: A decoding strategy that stops generation early based on a preset budget to save compute. "we test a budgeted decoding abstention mechanism that halts generation once a fixed token budget is reached."
- Accuracy–efficiency trade-off: The balance between task performance and computational cost for training or inference. "we move beyond raw accuracy to analyze the accuracyâefficiency trade-off."
- AIME: American Invitational Mathematics Examination; used as a challenging math benchmark for LLMs. "gsm8k, math-500, and aime"
- Aqua-RAT: A dataset of algebraic word problems with rationales used to evaluate mathematical reasoning. "In the mathematical domain, MC benchmarks include aqua-rat \citep{aquarat}, mmlu-math \citep{mmlu}, and mmlu-pro-math \citep{mmlupro}, while OE benchmarks include gsm8k \citep{gsm8k}, math-500 \citep{math500}, and aime \citep{aime}."
- Bi-phasic strategies: A two-stage training approach where a model is further trained on a domain after general training. "we study bi-phasic strategies in which models are further trained on a targeted domain starting from checkpoints pretrained on general-distribution data"
- Causal LLM: An autoregressive model that predicts the next token given previous tokens. "we adopt the standard prompt-based generation setting, where a causal LLM $f_{\bm{\theta}: \Omega^* \rightarrow \mathbb{R}^{|\Omega|}$ maps an input text sequence to unnormalized logit scores for next-token prediction."
- Catastrophic forgetting: The degradation of previously learned capabilities when fine-tuning on new data. "models below 1.5B parameters exhibit signs of catastrophic forgetting \citep{Kirkpatrick_2017} under the same adaptation regime"
- Chain-of-Thought (CoT): Supervision that includes intermediate reasoning steps to improve problem solving. "LLMs that generate explicit Chains of Thought (CoT) have rapidly become a defining paradigm."
- Domain-specific alignment: Fine-tuning a model on a specific domain to improve in-domain performance. "Domain-specific alignment yields performance gains at larger model scales."
- Extra-token factor: The multiplicative increase in tokens generated when switching from concise IFT outputs to longer reasoning outputs. "X-axis: extra-token factor when switching from IFT to reasoning."
- FLOPs: A measure of computational cost based on floating-point operations. "we vary the proportion of reasoning instances to examine the trade-offs between performance and training cost in FLOPs."
- GSM8K: A benchmark of grade-school math word problems for evaluating reasoning. "while OE benchmarks include gsm8k \citep{gsm8k}, math-500 \citep{math500}, and aime \citep{aime}"
- IFT alignment: Post-training alignment using instruction-style data to encourage concise, instruction-following outputs. "Applying IFT alignment on a model that has already performed general-reasoning training results in performance that is at best comparable to two-stage IFT"
- Inference FLOPs: The compute cost measured in floating-point operations incurred during generation. "we evaluate accuracy with respect to inference FLOPs"
- Instruction Fine-Tuning (IFT): Supervised fine-tuning on instruction-following data to align model outputs with user directives. "We compare Instruction Fine-Tuning (IFT) and reasoning models of varying sizes"
- Kleene closure: The set of all finite-length sequences over a given vocabulary. "and its Kleene closure."
- LLM-as-a-Judge: Using a LLM to grade or evaluate outputs from other models. "we use Llama-3_1-Nemotron-Ultra-253B-v1 \citep{nemotron} as a judge model"
- Mixture-of-Experts (MoE): A model architecture that routes inputs to specialized expert subnetworks. "a state-of-the-art open-weight mixture-of-experts model, Qwen3-235B-A22B"
- Mixed training: Training that combines IFT and reasoning-style instances in the same phase. "Mixed training exhibits pronounced instability, as evidenced by higher variance in accuracy across reasoning ratios"
- MMLU: Massive Multitask Language Understanding benchmark; includes math subsets for reasoning evaluation. "mmlu-math \citep{mmlu}"
- MMLU-Pro: A harder, more robust variant of MMLU intended to better stress model understanding. "mmlu-pro-math \citep{mmlupro}"
- Nucleus sampling: A probabilistic decoding strategy (top-p) that samples from the smallest set of tokens whose cumulative probability exceeds p. "nucleus-sampling parameter "
- Pareto frontier: The set of configurations for which no other configuration simultaneously improves both accuracy and cost. "The Pareto frontier (black dashed lines) highlights efficient configurations, while those that lie in the red-shaded area are suboptimal."
- Pareto-optimal: A configuration that cannot be improved in one objective without worsening another. "IFT is always Pareto-optimal."
- Pareto-suboptimal: A dominated configuration that is worse in both accuracy and cost than some alternative. "The red-shaded region highlights configurations that are Pareto-suboptimal."
- PPO: Proximal Policy Optimization, an RL algorithm commonly used to fine-tune reasoning via rewards. "Methods such as TRPO, PPO, and GRPO optimize reasoning trajectories"
- Reasoning ratio: The fraction of training instances that use reasoning-style supervision. "with denoting the reasoning ratio."
- Reasoning traces: The step-by-step intermediate derivations generated or supervised during training. "disentangle the contribution of reasoning traces from confounding factors"
- Reinforcement Learning (RL) pipelines: End-to-end RL training processes used to improve reasoning beyond supervised traces. "sidestepping the cost of RL pipelines"
- Sequential training: Two-phase training where IFT precedes reasoning-style fine-tuning. "sequential training ($\mathcal{T}_{\mathrm{seq}$), where models are first trained on IFT- and then on reasoning-style data."
- Temperature (decoding): A parameter controlling randomness in sampling; higher values yield more diverse outputs. "under temperature "
- TRPO: Trust Region Policy Optimization, an RL method used to optimize policies with stability constraints. "Methods such as TRPO, PPO, and GRPO optimize reasoning trajectories"
- Three-shot setting: Prompting the model with three examples before asking the target question. "we evaluate them in a three-shot setting"
- Winogrande: An adversarial commonsense reasoning benchmark derived from the Winograd schema challenge. "For general-purpose MC tasks, we use winogrande \citep{winogrande}, openbookqa \citep{openbookqa}, and mmlu-misc."
- Zero-shot setting: Evaluating a model without providing task-specific examples in the prompt. "distilled models are evaluated in a zero-shot setting to directly measure distilled behaviors."
Collections
Sign up for free to add this paper to one or more collections.