Diffusion and Flow-based Copulas: Forgetting and Remembering Dependencies

Abstract: Copulas are a fundamental tool for modelling multivariate dependencies in data, forming the method of choice in diverse fields and applications. However, the adoption of existing models for multimodal and high-dimensional dependencies is hindered by restrictive assumptions and poor scaling. In this work, we present methods for modelling copulas based on the principles of diffusions and flows. We design two processes that progressively forget inter-variable dependencies while leaving dimension-wise distributions unaffected, provably defining valid copulas at all times. We show how to obtain copula models by learning to remember the forgotten dependencies from each process, theoretically recovering the true copula at optimality. The first instantiation of our framework focuses on direct density estimation, while the second specialises in expedient sampling. Empirically, we demonstrate the superior performance of our proposed methods over state-of-the-art copula approaches in modelling complex and high-dimensional dependencies from scientific datasets and images. Our work enhances the representational power of copula models, empowering applications and paving the way for their adoption on larger scales and more challenging domains.

• The paper introduces two novel copula constructions—Classification-Diffusion Copula (CDC) and Reflection Copula—that use stochastic processes to preserve marginals while modeling dependencies.
• It leverages an Ornstein-Uhlenbeck process and classifier-based density recovery to achieve superior log-likelihood and sampling performance, validated on both synthetic and image datasets.
• Empirical evaluations demonstrate scalability to very high dimensions, with maintained uniform marginals and improved density estimation and generative sampling over traditional copulas.

Diffusion and Flow-based Copulas: Forgetting and Remembering Dependencies

Introduction and Motivation

The paper introduces a novel framework for copula modeling based on diffusion and flow processes, specifically designed to address the limitations of existing copula models in capturing multimodal and high-dimensional dependencies. Copulas are essential for modeling inter-variable dependence while preserving dimension-wise marginals, with applications spanning weather forecasting, risk management, synthetic data generation, and multi-agent systems. Traditional copula models, such as Gaussian and vine copulas, impose restrictive assumptions and scale poorly with dimensionality, while deep copula models suffer from mode collapse and inefficient sampling in complex domains.

The authors propose two new copula constructions: the Classification-Diffusion Copula (CDC) and the Reflection Copula, both leveraging stochastic processes that progressively forget dependencies but maintain uniform marginals. These models are theoretically guaranteed to define valid copulas at all times and are empirically shown to outperform state-of-the-art copula approaches in both density estimation and sampling tasks.

Figure 1: Overview of proposed copula models. Forward processes forget inter-variable dependencies but preserve marginals; copula models learn to remember the forgotten dependencies.

Classification-Diffusion Copula: Density Estimation and Sampling

The CDC is constructed by mapping copula data to the Gaussian scale and applying an Ornstein-Uhlenbeck (OU) process, which independently diffuses each dimension while preserving marginal distributions. The process is discretized into $k$ time steps, each representing a level of dependency decay. A multinomial classifier $c_{dc}$ is trained to predict the diffusion time $t$ from the data, effectively learning the copula density as a ratio of class probabilities.

Figure 2: Classifier-Diffusion Copula. Copula data is mapped to Gaussian scale, diffused via OU process, and classified to recover copula density.

Key theoretical results include:

• Marginal Preservation: The OU process ensures that marginals remain standard Gaussian (and thus uniform on the copula scale) at all times.
• Convergence to Independence: The copula converges to the independence copula at a rate $\mathcal{O}(e^{-2t})$ in KL divergence.
• Density Recovery: The copula density at a point is given by the ratio of the classifier's probability of the initial and terminal time classes.
• Score-based Sampling: The copula score for Langevin dynamics is expressed in terms of gradients of the classifier's output, enabling efficient diffusion-based sampling.

The CDC is trained using a mixture loss combining cross-entropy for time classification and mean squared error for score matching, ensuring both accurate density estimation and high-fidelity sampling. The approach is scalable to high dimensions due to the efficiency of diffusion-based sampling under the manifold hypothesis.

Reflection Copula: Fast Generative Sampling

The Reflection Copula is designed for expedient sampling by directly operating on the copula hypercube $[0,1]^d$. Each sample is assigned a random velocity and evolves via deterministic reflection within the hypercube, ensuring uniform marginals at all times. As time progresses, the process forgets dependencies and converges to the independence copula.

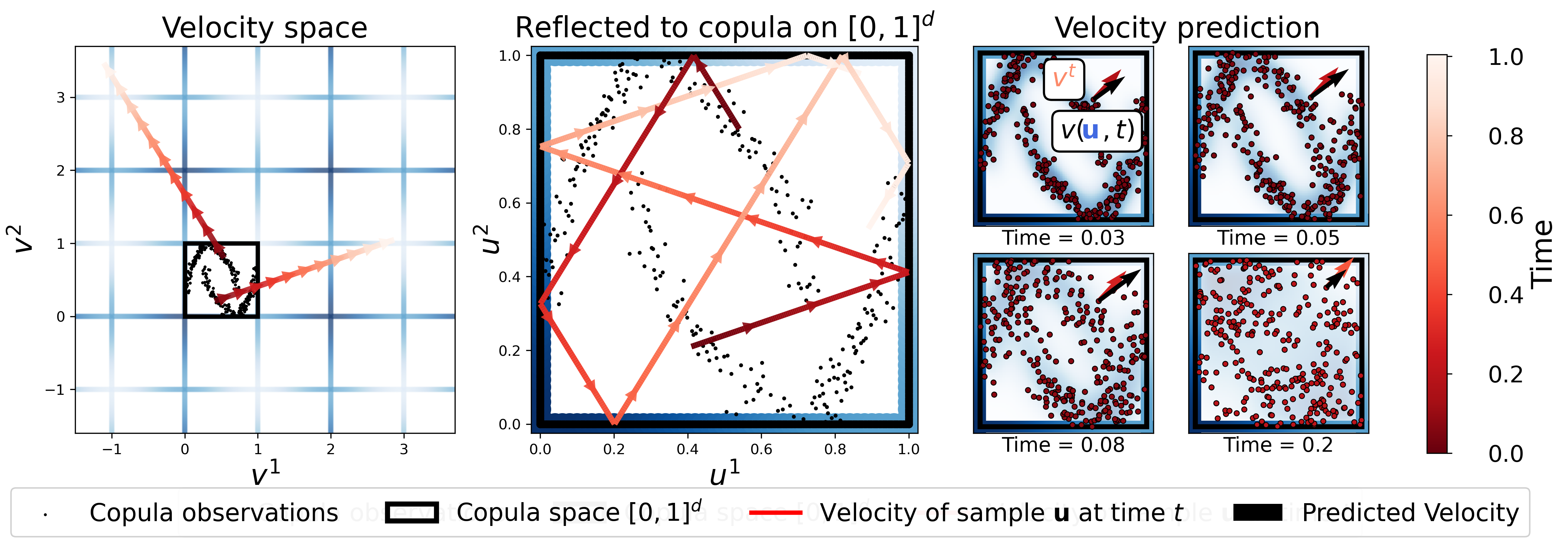
Figure 3: Reflection copula design. Copula data is assigned velocities, reflected within the hypercube, and diffused over time; a velocity predictor learns the average velocity for sampling.

Sampling is performed by numerically integrating the expected velocity field backwards from the stationary distribution (uniform samples) to the initial copula distribution. The velocity predictor is trained via mean squared error against true sample velocities, recovering the average velocity required for generative sampling.

Empirical Evaluation

The proposed models are evaluated on scientific datasets (Magic, Dry_Bean, Robocup) and high-dimensional image datasets (digits, MNIST, Cifar). Metrics include copula log-likelihood (LL), Wasserstein-2 distance (W2), Frobenius norm of Kendall's tau matrices, and Frechet Inception Distance (FID) for images.

Key empirical findings:

• CDC achieves superior LL evaluations compared to Gaussian, vine, ratio, and implicit generative copulas, especially in high dimensions.
• Both CDC and Reflection Copula produce samples with lower W2 and FID, indicating better modeling of complex dependencies.
• Uniformity diagnostics confirm that both models maintain uniform marginals, a critical property for valid copula sampling.
• Scalability: The models are the first copulas to scale to $d>1000$ dimensions and capture structured dependencies in image data.

Figure 4: Copula image samples. Only the proposed designs accurately represent complex dependencies in MNIST and Cifar datasets.

Theoretical and Practical Implications

The framework establishes a principled connection between copula modeling and diffusion/flow processes, enabling:

• Modular multivariate modeling: Marginals can be modeled independently, with dependence injected via copulas learned from stochastic processes.
• Efficient density estimation and sampling: CDC provides direct density evaluation and score-based sampling; Reflection Copula offers fast generative sampling.
• Interpretability and flexibility: The models isolate inter-variable dependencies, facilitating analysis in scientific and engineering domains.

The approach is theoretically grounded, with proofs of marginal preservation, convergence, and optimality of the learning objectives. The use of diffusion and flow principles opens avenues for further research in copula modeling, including extensions to discrete variables and alternative marginal-preserving processes.

Limitations and Future Directions

While the processes guarantee valid copulas by design, model parameterizations are only guaranteed to represent copulas at optimality. Open questions remain regarding architectural choices that enforce uniformity and normalization for arbitrary parameterizations. Extensions to discrete copulas and exploration of alternative stochastic processes for extreme dependence are promising directions.

Conclusion

The paper presents a rigorous framework for copula modeling via diffusion and flow-based processes, overcoming the limitations of existing models in high-dimensional and multimodal settings. The Classification-Diffusion Copula and Reflection Copula provide state-of-the-art performance in both density estimation and sampling, with theoretical guarantees and empirical validation. The methodology paves the way for scalable, interpretable, and flexible copula models in diverse scientific and engineering applications.