CAR-Flow: Condition-Aware Reparameterization Aligns Source and Target for Better Flow Matching (2509.19300v1)
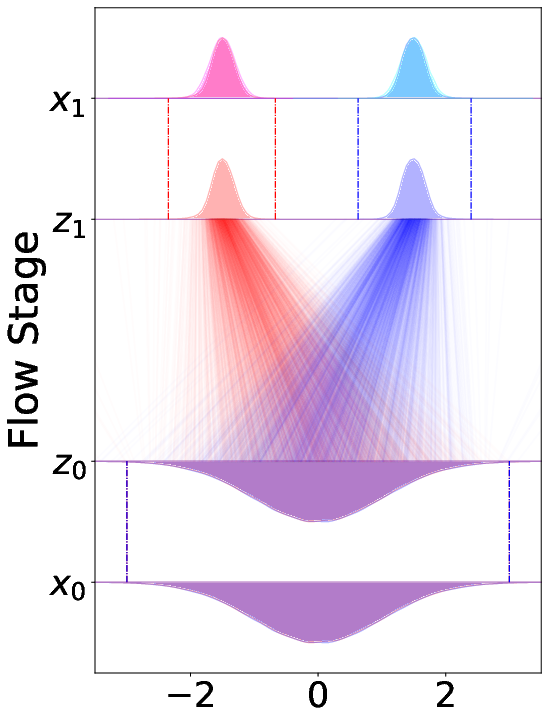
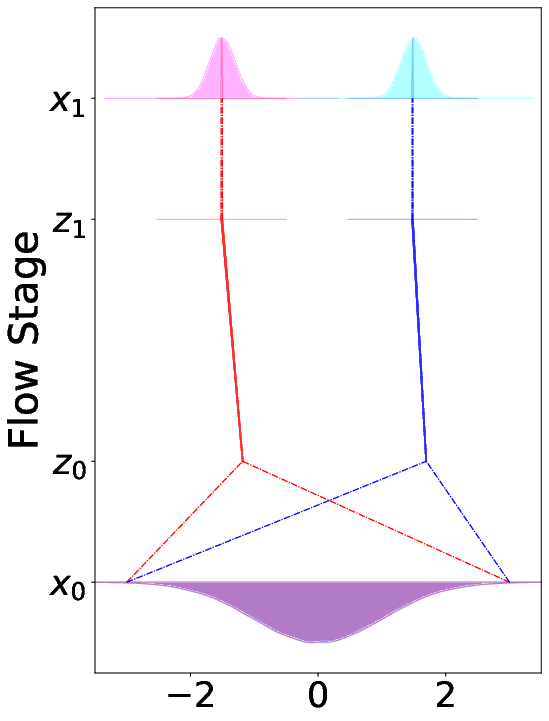
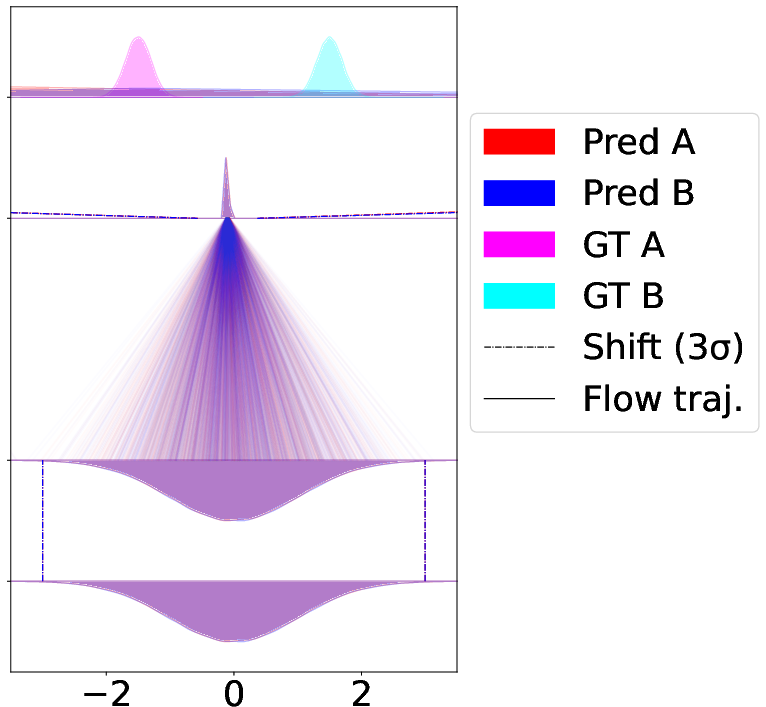
Abstract: Conditional generative modeling aims to learn a conditional data distribution from samples containing data-condition pairs. For this, diffusion and flow-based methods have attained compelling results. These methods use a learned (flow) model to transport an initial standard Gaussian noise that ignores the condition to the conditional data distribution. The model is hence required to learn both mass transport and conditional injection. To ease the demand on the model, we propose Condition-Aware Reparameterization for Flow Matching (CAR-Flow) -- a lightweight, learned shift that conditions the source, the target, or both distributions. By relocating these distributions, CAR-Flow shortens the probability path the model must learn, leading to faster training in practice. On low-dimensional synthetic data, we visualize and quantify the effects of CAR. On higher-dimensional natural image data (ImageNet-256), equipping SiT-XL/2 with CAR-Flow reduces FID from 2.07 to 1.68, while introducing less than 0.6% additional parameters.
Summary
- The paper introduces a method for condition-aware reparameterization by applying learnable additive shifts to align source and target distributions and reduce transport distance.
- It details three variants—source-only, target-only, and joint—with the joint variant achieving the fastest convergence and best sample quality while using minimal extra parameters.
- Experimental evaluations on synthetic data and ImageNet demonstrate faster convergence, lower Wasserstein errors, and improved FID scores compared to baseline flow-matching methods.
CAR-Flow: Condition-Aware Reparameterization Aligns Source and Target for Better Flow Matching
Introduction and Motivation
Conditional generative modeling, particularly in the context of diffusion and flow-based models, requires the transformation of a simple, condition-agnostic source distribution (typically a standard Gaussian) into a complex, condition-dependent target distribution. The conventional approach burdens the neural velocity field with both mass transport and semantic injection, which can lead to inefficient learning and suboptimal sample quality, especially when the conditional distributions are widely separated in the data manifold.
CAR-Flow introduces a principled solution: lightweight, learnable, condition-aware shifts applied to the source, the target, or both distributions. This reparameterization shortens the probability path that the model must learn, thereby accelerating convergence and improving sample fidelity. The approach is theoretically motivated by an analysis of failure modes in unrestricted reparameterization, which can lead to trivial, collapsed solutions. By restricting the reparameterization to additive shifts, CAR-Flow eliminates these degenerate minima while retaining the benefits of condition-aware alignment.
Methodology: Condition-Aware Reparameterization
CAR-Flow generalizes the flow-matching framework by introducing explicit, condition-dependent maps for the source and target distributions. Formally, the source distribution is reparameterized as and the target as , where and are lightweight neural networks producing additive shifts and , respectively. The push-forward chain replaces the direct mapping of standard flow matching.
This reparameterization is restricted to shift-only transformations:
where and are learnable functions of the conditioning variable . This restriction is critical to avoid mode collapse, as proven analytically in the paper.
Three CAR-Flow variants are considered:
- Source-only: Only the source is shifted ().
- Target-only: Only the target is shifted ().
- Joint: Both source and target are shifted.
Each variant alters the probability path in a distinct manner, with the joint variant providing the most effective alignment and shortest transport distance.
Theoretical Analysis: Avoiding Trivial Solutions
Unrestricted reparameterization admits several trivial zero-cost minima, including constant source/target, unbounded scale, and proportional collapse. These degenerate solutions result in the collapse of the generative distribution to a single or improper mode, rendering the velocity field parameter-independent and destroying sample diversity. The paper provides a formal proof that restricting and to additive shifts blocks all such collapse modes, ensuring that the learned flow remains expressive and nontrivial.
Empirical Evaluation: Synthetic Data
On 1D synthetic data, CAR-Flow demonstrates clear improvements over the baseline rectified flow. The source-only variant relocates the source distribution per class, the target-only variant unifies the trajectory endpoints, and the joint variant achieves the best alignment and flow quality, as visualized in learned flow trajectories.
Figure 1: Learned flow trajectories on 1D synthetic data for baseline and CAR-Flow variants, illustrating improved alignment and reduced transport distance.
Quantitatively, CAR-Flow variants yield significantly shorter average trajectory lengths compared to the baseline, with the joint variant achieving the minimal path. Convergence analysis using Wasserstein distance shows that joint CAR-Flow converges fastest and reaches the lowest error.
Figure 2: Wasserstein distance between predicted and ground-truth distributions, showing accelerated convergence for CAR-Flow variants.
The learned shifts and are moderate and balanced in the joint variant, explaining its superior performance.
Mode Collapse Diagnostics
Allowing both shift and scale parameters in the reparameterization triggers rapid mode collapse, as evidenced by the evolution of learned standard deviations and validation error. The network quickly discovers shortcut solutions by shrinking to zero, aligning with the analytic zero-cost solutions.
Figure 3: Learned scale dynamics, demonstrating rapid collapse when scale is unconstrained.
Large-Scale Evaluation: ImageNet
On ImageNet , CAR-Flow is integrated into the SiT-XL/2 backbone with minimal additional parameters (). All CAR-Flow variants outperform the baseline in FID, IS, sFID, precision, and recall, with the joint variant achieving the best results (FID reduced from 2.07 to 1.68).
CAR-Flow also accelerates optimization, with all variants converging faster than the baseline across training steps.
Figure 4: FID vs. training steps on ImageNet , showing faster convergence for CAR-Flow variants.
Implementation Details
CAR-Flow is straightforward to implement. For synthetic data, the shift networks are single-layer MLPs mapping class embeddings to scalar shifts. For ImageNet, lightweight convolutional networks predict the shifts from class embeddings to the latent space. The shift networks are initialized with zero weights and trained with higher learning rates than the backbone, which is critical for rapid alignment.
Sampling proceeds by drawing , applying the source shift, integrating the reparameterized SDE, and mapping back via the inverse target shift. The approach is compatible with existing flow-matching and diffusion frameworks and can be applied on top of pretrained VAEs.
Practical Implications and Future Directions
CAR-Flow provides a simple yet effective mechanism for condition-aware alignment in flow-matching models, relieving the neural velocity field of unnecessary transport and semantic encoding. The approach is computationally efficient, easy to integrate, and robust against mode collapse. Theoretical analysis and empirical results support its efficacy across synthetic and large-scale datasets.
Future work may explore more expressive, yet nontrivial, reparameterizations beyond additive shifts, potentially yielding further improvements in sample quality and convergence speed. The framework is compatible with recent advances in latent-space conditioning and representation alignment, suggesting broad applicability in generative modeling.
Conclusion
CAR-Flow introduces condition-aware reparameterization for flow matching, aligning source and target distributions via lightweight, learnable shifts. This approach alleviates the dual burden on the velocity network, accelerates convergence, and improves sample fidelity, all while avoiding trivial collapse solutions. The method is theoretically sound, empirically validated, and readily applicable to large-scale generative models. Further exploration of more general mappings may yield additional gains in expressivity and performance.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces a simple idea to make AI image generators learn faster and produce better results when they are told what to make (for example, “a cat” or “a car”). The authors call their method CAR-Flow. It gently “shifts” where the model starts and where it aims to finish based on the given condition (like the class label), so the model has an easier job turning random noise into the right kind of picture.
What problem are they trying to solve?
Modern image generators often start from the same kind of random noise for every request, even when the request (the condition) is different. That means the model has to do two hard things at once:
- Move from random noise to a realistic image.
- Inject the specific meaning of the condition (e.g., “dog” vs. “bicycle”).
Because different conditions often live in very different “areas” of the image space, learning both tasks at once can make training slow and results worse. The paper asks:
- Can we make the starting noise or the target space “aware” of the condition to shorten the path the model must learn?
- How do we do this safely, so the model doesn’t “cheat” and collapse into boring, same-looking outputs?
- Does this idea improve quality and training speed on small and large datasets?
How does their method work? (Explained simply)
Think of generating an image as following a route on a map:
- The usual approach starts at the same spot for every trip (same random noise), then the model learns a route to the final destination (the requested image).
- CAR-Flow says: “If we already know where we want to go, let’s pick smarter starting and ending spots that depend on the condition, so the route is shorter.”
More concretely:
- “Flow matching” is the technique that trains a model to follow a smooth path from noise to the target image. You can imagine a field of tiny arrows that tell the model which way to move at every step.
- “Reparameterization” here means we shift the start or the end point based on the condition (like a tiny nudge on the map), so the learned path is easier.
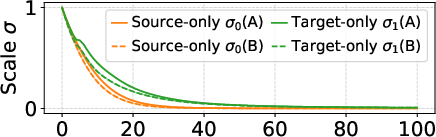
- Crucially, they only use “shift-only” changes (like moving a point left/right/up/down), without any “scale” changes (no zooming in/out). This matters because:
- If you allow very flexible changes (especially scaling), the training can find a lazy shortcut that collapses all outputs to the same thing (called “mode collapse”). That gives a low training loss but terrible results.
- By using shift-only changes, CAR-Flow avoids these collapse problems while still making training easier.
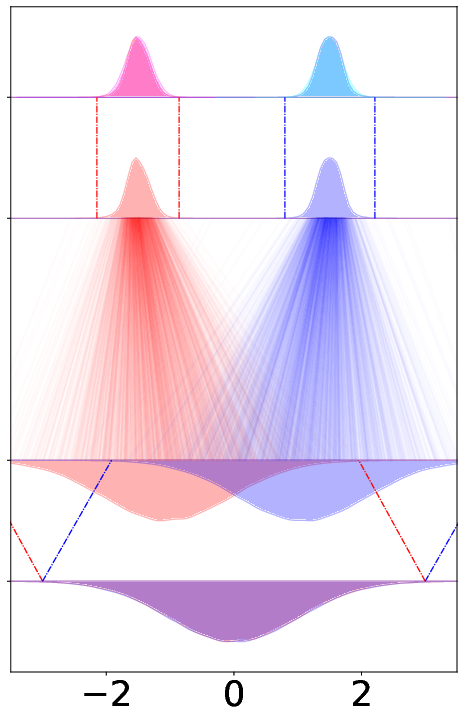
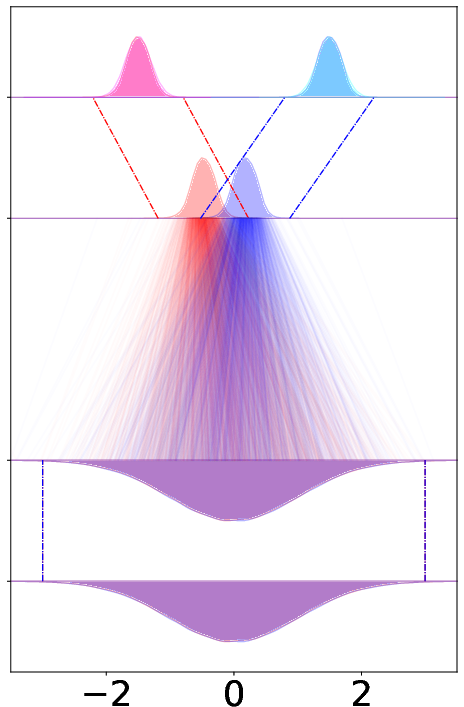
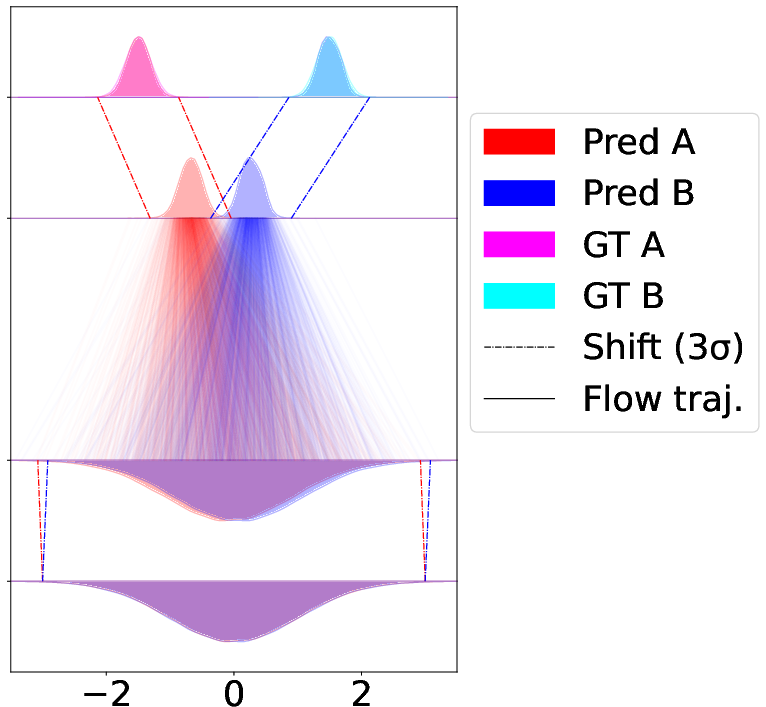
They try three variants:
- Source-only shift: shift the starting noise based on the condition.
- Target-only shift: shift the destination space based on the condition.
- Joint shift: shift both. This usually works best.
What did they test and what did they find?
They run two types of experiments:
1) Synthetic toy example (very simple 1D data)
- This is like practicing on a tiny problem where there are two classes far apart.
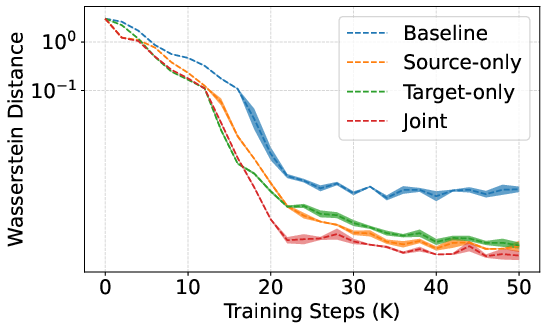
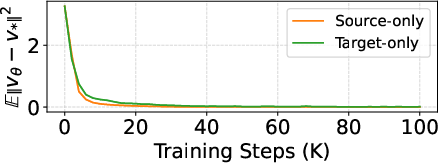
- CAR-Flow makes the path between the start and end much shorter, so the model learns faster and ends up more accurate.
- The “joint” version (shifting both start and end) gives the shortest path and best results.
2) Real images (ImageNet at 256×256 resolution)
- They add CAR-Flow to a strong baseline model called SiT-XL/2.
- With CAR-Flow, the image quality improves. One key metric, FID (a number that rates how realistic and varied the generated images are), drops from 2.07 to 1.68. Lower is better.
- CAR-Flow adds less than 0.6% more parameters, so it’s a tiny change with a big effect.
- Training also converges faster: the model reaches good quality sooner.
Why is this important?
- Shorter paths mean the model has an easier job. It doesn’t have to “drag” random noise all the way across the image space to the right spot.
- That leads to faster training and better images, with almost no extra cost.
What does this mean going forward?
This work suggests a simple, safe way to help conditional image generators: make the starting point and destination a little “aware” of the request with tiny learned shifts. This:
- Improves image quality.
- Speeds up training.
- Is easy to plug into existing systems because it adds very little complexity.
The authors also warn that more flexible changes (like scaling) can cause collapse (everything looks the same). Their shift-only rule avoids that, but in the future, smarter safe rules might allow even more powerful conditioning without risking collapse.
Quick summary of the CAR-Flow variants
Here is a brief overview to help you remember the three versions:
| Variant | What it shifts | Intuition | Typical result |
|---|---|---|---|
| Source-only | Starting noise | Start closer to the right region for that class | Better than baseline |
| Target-only | Destination space | Endpoints line up better across conditions | Better than baseline |
| Joint (both) | Start and destination | Shortest path end-to-end | Best overall |
Overall, CAR-Flow is like giving the model a smarter start and finish line tailored to the request, so it runs a shorter race and wins more often.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
The following list highlights what remains missing, uncertain, or unexplored, with concrete directions for future work:
- Limited conditioning scope: CAR-Flow is only validated for class-conditional ImageNet-256; its effectiveness on richer conditioning (e.g., text prompts, semantic masks, multi-label conditions), other modalities (audio, video), and higher resolutions remains untested.
- Generalization across base architectures: Results are reported for SiT-XL/2; performance, stability, and integration challenges with other flow/diffusion backbones (e.g., DiT, SDXL, rectified-flow variants, unconditional models) are unknown.
- High-dimensional collapse diagnostics: The collapse analysis and experiments are restricted to 1D synthetic data; whether similar trivial minima emerge in high-dimensional, real datasets under unrestricted reparameterization—and how to robustly detect/avoid them—remains open.
- More expressive yet safe reparameterizations: Only shift-only conditioning is explored; the design space of “collapse-proof” mappings (e.g., bounded affine transforms, orthogonal/volume-preserving linear maps, low-rank shifts, constrained normalizing flows, time-dependent but regulated shifts) is uncharted.
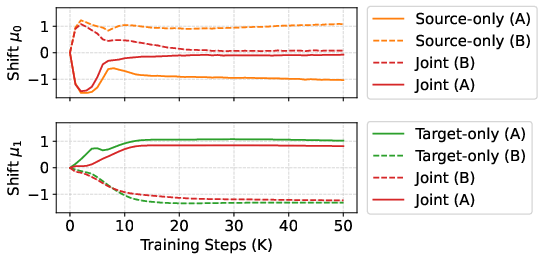
- Identifiability and parameter coupling: The decomposition into source shift μ₀(y) and target shift μ₁(y) may be non-identifiable; understanding redundancy, parameter sharing, or regularization (e.g., priors, penalties, sparsity) needed to make the two shifts uniquely attributable is missing.
- Learning time-dependent shifts: CAR-Flow uses μ_t(y)=β_t μ₀(y)+α_t μ₁(y); learning μ_t(y) directly as a function of (t,y) with constraints (to prevent collapse) is unexplored.
- Noise schedules: Experiments use a linear schedule; the impact of alternative schedules (e.g., cosine, data-adaptive, learned schedules) on path length, convergence speed, and stability under CAR-Flow is not studied.
- Empirical path-shortening in high dimensions: Path-shortening is quantified only in 1D; measuring in high-dimensional latents (e.g., average trajectory length, kinetic energy, Wasserstein distance over training, FöLLMer drift energy) would substantiate the claimed mechanism at scale.
- Interaction with classifier-free guidance (cfg): CAR-Flow’s behavior across guidance scales, its effect on precision/recall trade-offs, and whether cfg hyperparameters require re-tuning under CAR-Flow are not analyzed.
- Solver sensitivity: Robustness across samplers (ODE vs SDE), solvers (Euler, Heun, DDIM-style), NFEs, and step schedules is not assessed; CAR-Flow could alter numerical stiffness or stability.
- Wall-clock efficiency: While faster convergence in FID is shown, there is no report of wall-clock speedups, TPU/GPU-hours to reach target metrics, or throughput changes due to the shift nets.
- Inference overhead: The added μ-networks introduce minimal parameter overhead, but the runtime cost and memory footprint during sampling (especially in distributed settings) are not quantified.
- VAE dependence and invertibility: Using sd-vae-ft-ema as g/g⁻¹ assumes “approximate invertibility”; the reconstruction error distribution, its condition-dependence, and impact on sample quality and diversity under CAR-Flow are not measured.
- Robustness to VAE choice and latent dimensionality: How CAR-Flow’s benefits vary with different VAEs, latent sizes, and encoder/decoder training regimes (frozen vs fine-tuned) is unknown.
- Regularization of shifts: There is no ablation on regularizing μ₀/μ₁ (e.g., magnitude penalties, Lipschitz constraints, conditioning norm budgets) to prevent pathological large shifts, overfitting, or training instabilities.
- Per-class and long-tail behavior: Aggregate metrics improve, but per-class FID/recall, mode coverage across conditions, and performance on rare classes are not reported.
- OOD and zero-shot conditions: How CAR-Flow behaves for unseen or weakly represented conditions (e.g., new class labels, domain shifts) and whether learned shifts generalize or fail catastrophically is unexamined.
- Bias and fairness: Condition-aware shifts could encode or amplify dataset biases; fairness audits (e.g., subgroup metrics, stereotyping artifacts) and mitigation strategies are absent.
- Theoretical guarantees: Beyond blocking the collapse modes in Claim 1, formal guarantees (e.g., absence of other degenerate minima under shift-only, convergence rate improvements, bounds on path length reduction) are not provided.
- Safety margins for “safe” reparameterizations: Clear criteria for what constraints suffice to avoid trivial minima (e.g., bounded scale, orthogonality, determinant constraints) are not characterized; a principled taxonomy of safe mappings is needed.
- Diagnostics for collapse during training: Practical tools to detect impending collapse (e.g., monitoring variance in p_z, alignment of v_θ with zero-cost forms, μ/σ dynamics) in large-scale runs are not proposed.
- Interpretability of learned shifts: In high-dimensional latents, the semantic meaning of μ₀/μ₁, their alignment with condition embeddings, and how they move samples relative to class manifolds are not analyzed.
- Hyperparameter sensitivity: The sensitivity of CAR-Flow to μ-network architecture, learning rates, weight decay, and conditioning embedding choices is not explored.
- Data and resolution breadth: Validation is limited to ImageNet 256×256; scaling to higher resolutions (512, 1024), other datasets (CIFAR-10/100, LSUN, COCO), and multimodal corpora remains untested.
- Robustness to training recipes: The method is tied to a specific SiT recipe; its resilience to different optimization settings (optimizer type, batch size, augmentation, EMA usage) is unknown.
- Quantifying diversity improvements: Recall slightly improves, but broader diversity metrics (e.g., coverage, density, intra-class diversity) and qualitative analyses (mode dropping vs fidelity) are missing.
- Failure modes under partial fine-tuning: The paper relates to end-to-end VAE–diffusion training failures but does not systematically evaluate CAR-Flow under various partial fine-tuning regimes (e.g., fine-tuning encoder only, decoder only, or μ-nets only).
- Extensions beyond additive shifts: Exploring structured per-dimension shifts, attention-conditioned shifts, or content-aware shifts (dependent on x as well as y) under constraints that provably avoid collapse is left open.
Practical Applications
Practical Applications of CAR-Flow: Condition-Aware Reparameterization for Flow Matching
CAR-Flow introduces lightweight, condition-dependent shifts to the source and/or target distributions in flow/diffusion models. This shortens the learned probability path, speeds up training, improves fidelity, and avoids trivial collapse modes that can arise in naive end-to-end VAE–diffusion training. Below are concrete applications, categorized by time horizon, with sector links, potential tools/workflows, and feasibility notes.
Immediate Applications
- Drop-in quality and efficiency upgrade for existing image generation pipelines
- Sectors: software, media/creative, advertising
- What: Integrate source/target shift heads into SiT/DiT/Stable Diffusion–style latent pipelines to reduce FID and improve convergence (e.g., SiT-XL/2 + CAR-Flow: FID 2.07 → 1.68 with <0.6% extra params).
- Tools/workflows:
- Add two small “shift heads” to predict μ0(y) and μ1(y) from condition embeddings (class/text) and modify the loss to use reparameterized z-space (z0 = x0 + μ0(y), z1 = E(x1) + μ1(y)); sample with x1 = D(z1 − μ1(y)).
- Maintain the same sampler/solver (e.g., Heun SDE or Euler) and conditioning stack; treat CAR as a pluggable module or LoRA-like adapter for VAEs.
- Assumptions/dependencies: Access to a pretrained, approximately invertible encoder/decoder (VAE); condition embeddings available (class, text, mask); careful enforcement of shift-only (no scaling) to avoid collapse.
- Faster training and compute/carbon savings
- Sectors: software infrastructure, MLOps, policy/ESG
- What: Shorter probability paths yield faster convergence, lowering GPU/TPU hours and energy use for large-scale model training/fine-tuning.
- Tools/workflows: Incorporate CAR-Flow into training recipes; track wall-clock/step FID curves; integrate with schedulers to early-stop on convergence targets.
- Assumptions/dependencies: Benefits are largest where conditions are semantically distinct and the baseline path is long; gains depend on solver and hardware efficiency.
- Stabilized end-to-end VAE–diffusion fine-tuning
- Sectors: software/ML research, foundation models
- What: Use shift-only reparameterization to avoid zero-cost collapse modes identified by the paper when jointly training encoders/decoders with diffusion/flow models.
- Tools/workflows:
- Train μ-heads jointly with the backbone; keep scales fixed (no learned σ) to preclude collapse.
- Add collapse diagnostics (monitor variance in z-space, detect constant-map behavior; compare predicted velocity vs. analytic zero-cost forms).
- Assumptions/dependencies: Requires discipline in parameterization (shift-only) and training-time checks; collapse prevention is theoretical plus empirically validated for images.
- Better controllability in class/text/mask-conditional generation
- Sectors: media/creative, e-commerce, gaming
- What: Improved alignment at trajectory start and end simplifies “semantic injection,” improving prompt/class consistency and diversity without parameter bloat.
- Tools/workflows:
- For prompt-conditioned models, predict μ from text encoder features (e.g., CLIP/T5).
- For mask/segmentation conditioning, predict μ from spatial condition embeddings to align target regions in latent space.
- Assumptions/dependencies: Quality depends on condition encoder fidelity; spatially structured conditions might benefit from per-token/per-region shift maps.
- Synthetic data augmentation for vision tasks
- Sectors: retail, manufacturing, autonomous driving, security
- What: Produce higher-fidelity, class-balanced synthetic images with fewer resources to bolster downstream classifiers/detectors.
- Tools/workflows: Fine-tune μ-heads on rare classes or domains; fix backbone to minimize drift; evaluate gains on mAP/Top-1.
- Assumptions/dependencies: Must validate domain shift and label fidelity; ensure licensing/compliance for training data.
- On-device or low-footprint generation
- Sectors: mobile, XR, edge computing
- What: Minimal parameter overhead for CAR makes it suitable for on-device adapters that improve quality/controllability without deploying large new models.
- Tools/workflows: Ship μ-heads as small adapters; quantize heads; keep VAE and backbone shared across apps.
- Assumptions/dependencies: Device has a compatible VAE backbone and prompt encoder; latency budget still dominated by backbone.
- A/B testing and personalization in marketing pipelines
- Sectors: advertising, e-commerce
- What: Better class/prompt conditioning with small finetunes to μ-heads for brand/style/palette personalization.
- Tools/workflows: Train per-brand μ-heads with few-shot examples; measure lift in CTR/conversion; rollback is easy by disabling heads.
- Assumptions/dependencies: Requires brand-safe prompt templates and human-in-the-loop review.
- Training diagnostics and evaluation standards
- Sectors: academia, ML toolchains
- What: Use the paper’s collapse taxonomy to design unit tests and monitors for reparameterized models.
- Tools/workflows:
- Implement alerts for σ-growth (if enabled) and constant-map behavior in f/g; log Wasserstein distances and trajectory lengths.
- Assumptions/dependencies: Requires access to intermediate latents; applies across frameworks (JAX, PyTorch).
Long-Term Applications
- Multimodal extension: video, audio, 3D
- Sectors: media/entertainment, AR/VR, speech
- What: Extend CAR-Flow to temporal/spatial latents (video diffusion, audio diffusion, NeRF/3D assets), conditioning on text, audio, or motion prompts.
- Tools/workflows:
- Predict time-varying μ for sequences; couple with per-frame or per-chunk conditioning; integrate with latent video VAEs.
- Assumptions/dependencies: Requires invertible or well-behaved decoders for new modalities; careful temporal consistency regularization.
- Robotics and motion planning with diffusion policies
- Sectors: robotics, logistics, autonomous systems
- What: Condition-aware shifts for initial/goal distributions reduce required transport, improving sample efficiency and control fidelity.
- Tools/workflows: Predict μ from task context (goal pose, affordances) and sensory state; integrate with diffusion policy training loops.
- Assumptions/dependencies: Must ensure safe, physically plausible trajectories; real-world validation and sim-to-real alignment needed.
- Scientific and engineering surrogates
- Sectors: climate/weather, energy grids, CFD, materials
- What: Conditioned on boundary conditions or coarse fields, CAR-Flow can shorten paths in generative surrogates (e.g., downscaling, PDE-conditioned generation).
- Tools/workflows: Embed boundary/forcing fields via encoders; predict μ to align source/target latent states; quantify error vs. solvers.
- Assumptions/dependencies: Requires scientifically grounded evaluation; domain-specific constraints/physics-informed regularization.
- Healthcare: privacy-preserving, conditional data synthesis
- Sectors: healthcare, biotech
- What: Generate medical images or tabular EHRs conditioned on demographics/pathology for data augmentation and scenario simulation with stronger controllability.
- Tools/workflows: Federated training of μ-heads; differential privacy; clinician-in-the-loop validation; bias/fairness audits by subgroups.
- Assumptions/dependencies: Strict regulatory compliance (HIPAA/GDPR); rigorous utility–privacy trade-off analysis; robust de-biasing.
- Finance: conditional tabular/time-series generation
- Sectors: finance, risk, insurance
- What: Scenario/stress-test generation conditioned on macro variables or regimes; shorter transport may stabilize training on sparse/rare regimes.
- Tools/workflows: Use tabular/time-series VAEs; predict μ from economic factors; evaluate on risk metrics and backtests.
- Assumptions/dependencies: High stakes; guardrails against hallucinations and leakage; clear lineage and audit logs.
- Generative design and configuration
- Sectors: CAD/PLM, automotive, fashion, architecture
- What: Condition on specs, constraints, or partial designs; μ-shifts align latent spaces to reduce iterations and improve constraint satisfaction.
- Tools/workflows: Pair with constraint-checkers; multi-condition μ (materials, tolerances, cost); loop with optimization.
- Assumptions/dependencies: Needs structured condition encoders; post-generation validation and manufacturability checks.
- Beyond shift-only: learnable, safe reparameterizations
- Sectors: academia, foundation model labs
- What: Explore richer, invertible target maps (e.g., constrained normalizing flows) or low-rank affine transforms with collapse-proof regularization.
- Tools/workflows: Penalize variance collapse; Jacobian/condition number constraints; curriculum from shift-only to mildly nonlinear maps.
- Assumptions/dependencies: Theoretical guarantees and scalable training; careful ablations to prevent new collapse routes.
- Personalized and federated adapters
- Sectors: mobile, privacy tech
- What: Train μ-heads per user/device to encode style or preference while keeping backbones frozen; federated aggregation without sharing raw data.
- Tools/workflows: Lightweight on-device optimization; secure aggregation; adapter marketplaces.
- Assumptions/dependencies: Privacy guarantees; cross-device heterogeneity; efficient personalization protocols.
- Governance, policy, and safety practices for reparameterized generative models
- Sectors: policy/regulation, platform governance
- What: Encourage reporting of reparameterization choices and collapse checks; integrate provenance/watermarking; assess misuse risk as fidelity improves.
- Tools/workflows:
- Standardized training cards: whether source/target were condition-aware, collapse diagnostics, carbon metrics from faster convergence.
- Watermark latents post-shift; content authenticity pipelines (e.g., C2PA).
- Assumptions/dependencies: Community adoption; alignment with platform policies and upcoming AI regulations.
- Active learning and curriculum schedules via μt
- Sectors: academia, MLOps
- What: Use time-varying shifts μt(y) as a curriculum knob (e.g., start with large alignment, anneal to zero to prevent overfitting).
- Tools/workflows: Schedule μ magnitudes; monitor trajectory length and FID vs. training steps; combine with sampler distillation.
- Assumptions/dependencies: Requires ablations to avoid hurting diversity; task-dependent schedules.
Notes on feasibility and dependencies across applications:
- Conditioning sources: Works best when conditions (labels/prompts/masks) are informative and well-embedded; quality of the condition encoder matters.
- Decoders: Approximate invertibility is needed for target mapping; VAEs are a practical choice today.
- Collapse prevention: Strictly enforce shift-only on reparameterizations unless using additional constraints; add training-time monitors.
- Generalization: While demonstrated on images, extensions to other modalities require appropriate latent spaces and decoders.
- Ethics and safety: Higher fidelity and controllability increase both utility and misuse potential; pair deployments with watermarking, provenance, and human oversight.
Glossary
- Adaptive normalization layers: Layers whose normalization parameters are modulated by a conditioning signal to inject semantics into a network. "where the condition is commonly incorporated via embeddings or adaptive normalization layers."
- Approximately invertible map: A mapping g that can be (approximately) inverted to recover data space samples from latent variables. "Critically, to make sampling tractable, must be approximately invertible"
- Classifier-Free Guidance (CFG): A sampling technique that scales conditional guidance to trade off fidelity and diversity; the scalar indicates guidance strength. "cfg=1.5"
- Conditional flow matching: Training a neural velocity field to follow a conditional probability path from a source to a target distribution. "Conditional flow matching trains a neural velocity field to approximate the true velocity "
- Conditional generative modeling: Learning a data distribution conditioned on an external variable (e.g., class label or text). "Conditional generative modeling aims to learn a conditional data distribution from samples containing data-condition pairs."
- Condition-Aware Reparameterization (CAR-Flow): The paper’s method: lightweight, learned shifts that make source/target distributions depend on the condition to ease transport. "we propose Condition-Aware Reparameterization for Flow Matching (CAR-Flow) -- a lightweight, learned shift"
- Data manifold: The structured subset of input space where realistic data reside; models transport mass to the correct region of it. "transporting probability mass to the correct region of the data manifold"
- Dirac delta: A distribution concentrated at a single point, used as an endpoint of the probability path. "Here denotes the Dirac delta ``distribution''."
- Drift field: The deterministic component of an SDE that directs the trajectory’s evolution. "where is the drift field"
- ELBO (Evidence Lower Bound): The VAE training objective combining reconstruction accuracy and a KL regularizer. "trained via the ELBO (reconstruction loss plus KL divergence)"
- Euler integrator: A first-order numerical method for ODEs used to simulate deterministic flows. "employ a 50-step Euler integrator for sampling."
- Euler–Maruyama: A numerical scheme for SDEs analogous to Euler’s method for ODEs. "/* e.g., EulerâMaruyama */"
- Flow matching: A framework that learns a velocity field to transport samples from a source to a target distribution. "flow matching is typically formulated in latent space"
- Gaussian path: A time-indexed sequence of Gaussian distributions used to define the transport trajectory. "A convenient instantiation is the Gaussian path."
- Heun SDE solver: A higher-order stochastic solver (the stochastic version of Heun’s method) used at sampling time. "All models are sampled using the Heun SDE solver with 250 NFEs."
- Interpolant: The explicit mixture of source and target samples parameterized by schedule functions along the path. "the state evolves by the interpolant"
- Isotropic Gaussian: A multivariate normal distribution with identity covariance, often used as the source prior. "A standard choice for the source distribution is the isotropic Gaussian"
- KL divergence: A measure of distributional difference used as a regularizer in the VAE objective. "ELBO (reconstruction loss plus KL divergence)"
- Latent diffusion model: A generative setup where diffusion is trained and sampled in the compressed latent space of a VAE. "To recover the standard latent diffusion model"
- Latent space: The compressed representation space produced by a VAE where flow matching can be performed. "the target distribution in latent space"
- Mass transport: Moving probability density from the source to the target distribution along a learned trajectory. "transporting probability mass"
- Mode collapse: A failure mode where the learned distribution degenerates to a single (or improper) mode. "Mode collapse diagnostics with scale reparameterization."
- Monotonic noise scheduling functions: Time-dependent functions controlling the interpolation and noise levels, monotonic over t. "be two continuously differentiable, monotonic noise scheduling functions"
- Number of function evaluations (NFEs): The count of solver calls during sampling; a measure of sampling cost. "with 250 NFEs."
- Ordinary differential equation (ODE): A deterministic differential equation; the zero-noise limit of an SDE. "this SDE reduces to the ODE"
- Probability path: The trajectory of intermediate distributions connecting source and target during generation. "trace a probability path"
- Push-forward (map/chain): The transformation of a distribution through a function, producing a new distribution in another space. "The resulting push-forward chain "
- Rectified flow: A practical flow-matching variant with strong empirical performance on large-scale data. "classic rectified flow"
- Score function: The gradient of the log-density, used in SDE formulations of diffusion/flow. "The term denotes the score function"
- Semantic alignment loss: An auxiliary loss aligning latent/features to semantic embeddings from foundation models. "augment VAE training with a semantic alignment loss"
- Semantic injection: The process of encoding semantic information into the generative trajectory or latent representation. "semantic injection at once"
- Source distribution map: A condition-dependent mapping that transforms the source prior into a y-aware latent source. "source distribution map "
- Stochastic differential equation (SDE): A differential equation with a stochastic term modeling diffusion/flow dynamics. "follows the SDE"
- Standard Wiener process: Brownian motion; the driving noise process in SDEs. "and is a standard Wiener process."
- Target distribution map: A condition-dependent mapping that embeds data into latent space for flow and inversion. "target distribution map "
- Velocity field: The vector field predicted by the network that guides transport along the path. "the model predicts a velocity field"
- Wasserstein distance: An optimal-transport metric for comparing distributions, used to assess convergence. "Wasserstein distance"
Collections
Sign up for free to add this paper to one or more collections.