A1: Asynchronous Test-Time Scaling via Conformal Prediction (2509.15148v1)

Abstract: LLMs benefit from test-time scaling, but existing methods face significant challenges, including severe synchronization overhead, memory bottlenecks, and latency, especially during speculative decoding with long reasoning chains. We introduce A1 (Asynchronous Test-Time Scaling), a statistically guaranteed adaptive inference framework that addresses these challenges. A1 refines arithmetic intensity to identify synchronization as the dominant bottleneck, proposes an online calibration strategy to enable asynchronous inference, and designs a three-stage rejection sampling pipeline that supports both sequential and parallel scaling. Through experiments on the MATH, AMC23, AIME24, and AIME25 datasets, across various draft-target model families, we demonstrate that A1 achieves a remarkable 56.7x speedup in test-time scaling and a 4.14x improvement in throughput, all while maintaining accurate rejection-rate control, reducing latency and memory overhead, and no accuracy loss compared to using target model scaling alone. These results position A1 as an efficient and principled solution for scalable LLM inference. We have released the code at https://github.com/menik1126/asynchronous-test-time-scaling.

• The paper introduces A1's core contribution: integrating conformal prediction for adaptive rejection sampling to mitigate synchronization overhead in speculative decoding.
• It refines arithmetic intensity metrics to evaluate asynchronous performance, demonstrating up to 56.7x speedup and 4.14x throughput improvements.
• The work provides theoretical guarantees for marginal and conditional coverage and outlines a scalable, three-stage pipeline for LLM inference.

Asynchronous Test-Time Scaling via Conformal Prediction: A1 Framework

Motivation and Problem Formulation

The A1 framework addresses the core inefficiencies in test-time scaling for LLMs, particularly in settings where speculative decoding is used to accelerate inference. Test-time scaling refers to the paradigm of allocating additional compute resources during inference, either sequentially or in parallel, to enhance model reasoning capabilities. While parallel scaling offers throughput gains, it introduces severe synchronization overhead, memory bottlenecks, and increased latency, especially when speculative decoding is combined with long reasoning chains.

A1 identifies synchronization as the dominant bottleneck in parallel speculative decoding. The framework introduces asynchronous arithmetic intensity as a metric to quantify the impact of synchronization and memory access on throughput and latency. The central technical contribution is the integration of @@@@1@@@@ for adaptive, statistically guaranteed rejection sampling, enabling asynchronous inference and precise control over the intervention rate of the target model.

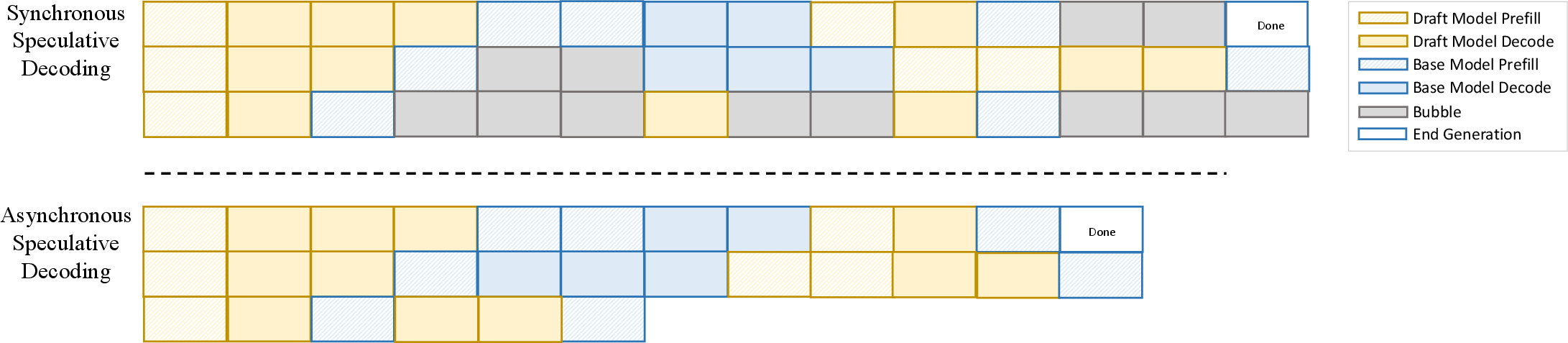
Figure 1: Comparison of naive and asynchronous speculative decoding, highlighting the reduction in synchronization bottlenecks with the A1 approach.

System Bottlenecks and Asynchronous Arithmetic Intensity

Speculative decoding accelerates inference by using a lightweight draft model to generate candidate tokens, which are then validated by a larger target model. In parallel scaling, the memory overhead of the target model grows rapidly due to KV cache accumulation, and synchronization delays from ranking and validation of multiple samples become the primary bottleneck.

A1 refines the classical arithmetic intensity metric ($I = F/B$) to account for synchronization costs, defining asynchronous arithmetic intensity $r = T_c / (T_m + T_s)$, where $T_c$ is computation time, $T_m$ is memory access time, and $T_s$ is synchronization time. Empirical analysis demonstrates that as sampling size increases, $r$ decreases, indicating that synchronization overhead dominates system performance in large-scale parallel speculative decoding.

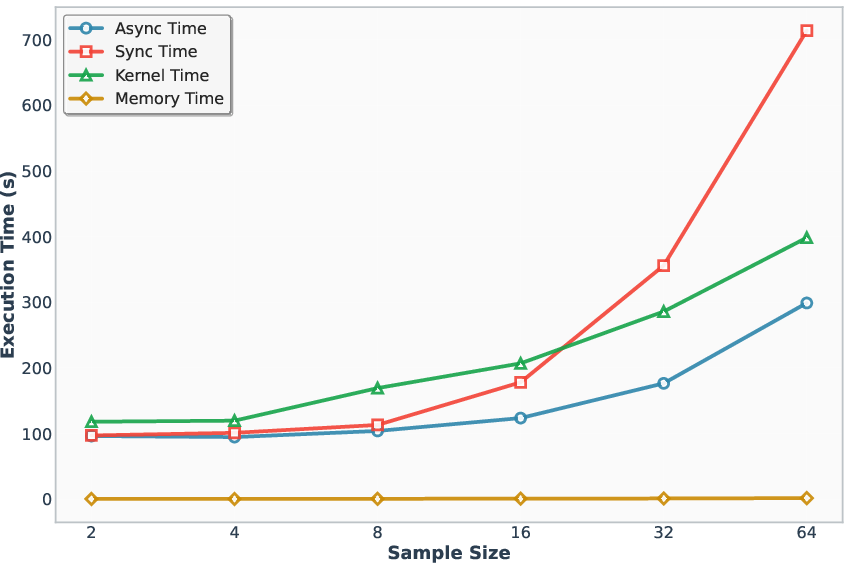
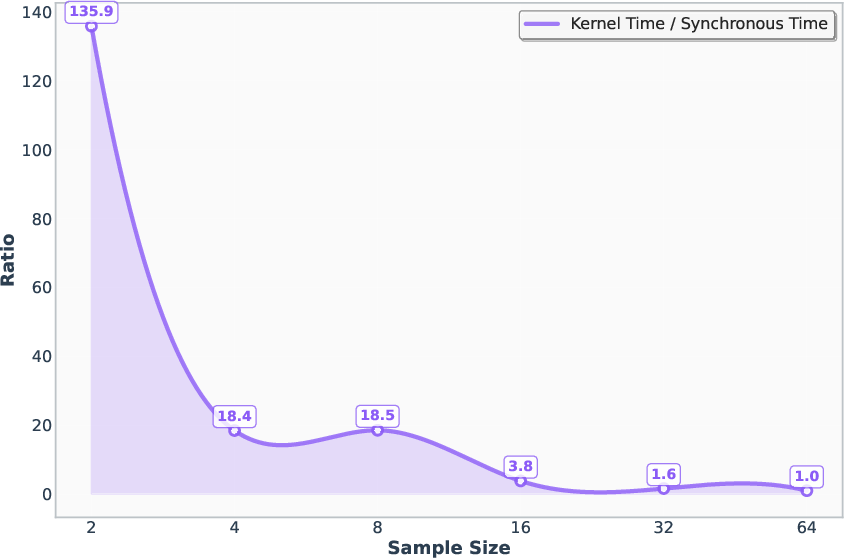
Figure 2: Arithmetic intensity vs. sampling size, showing the decline in asynchronous arithmetic intensity as synchronization costs increase.

Conformal Prediction for Adaptive Rejection Sampling

A1 leverages conformal prediction to construct prediction sets with guaranteed coverage, enabling precise control of the rejection rate during asynchronous inference. The framework supports both marginal and conditional coverage:

• Marginal Coverage: Guarantees that the prediction set contains the ground-truth with probability at least $1-\alpha$ over the test distribution.
• Conditional Coverage: Ensures coverage for each individual input instance.

The online calibration strategy eliminates the need for a held-out calibration set, instead using pre-sampled outputs to estimate conformity scores and quantile thresholds. Candidates are accepted if their conformal $p$-value exceeds the miscoverage threshold $\alpha$, allowing for asynchronous evaluation and rejection without global synchronization.

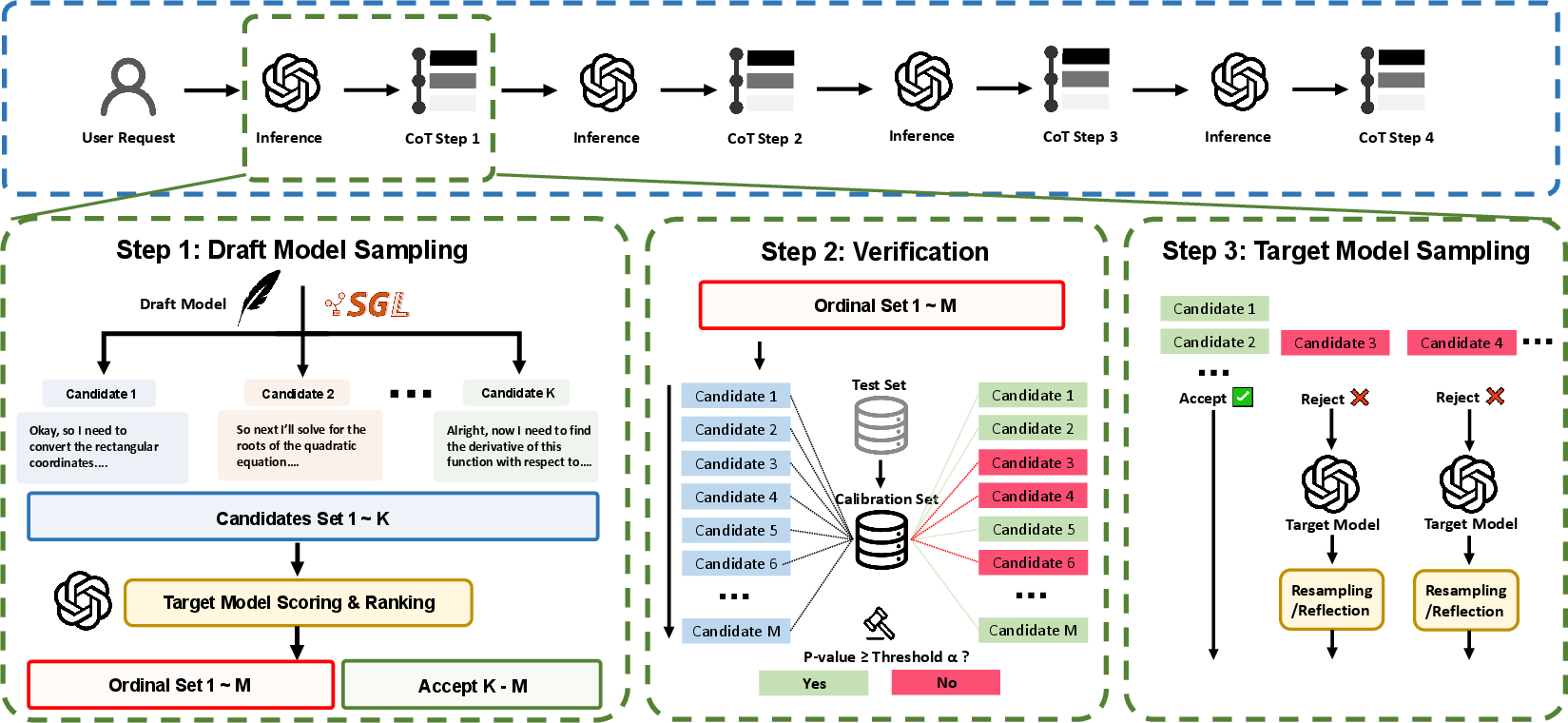
Figure 3: Asynchronous test-time scaling pipeline, illustrating parallel (green) and sequential (blue) scaling with rejection sampling.

Three-Stage Asynchronous Sampling Pipeline

The A1 pipeline consists of:

1. Draft Model Sampling: The draft model generates $m$ candidate continuations for each input.
2. Verification: The target model scores each candidate, computes conformity scores, and applies rejection sampling based on conformal $p$-values.
3. Target Model Sampling: Accepted candidates are continued by the target model, with per-round token budgets enforced.

This process is iterated until a final answer is produced or resource limits are reached. The pipeline supports both parallel and sequential scaling, with the number of candidates and turns controlling the scaling mode.

Empirical Results and Performance Analysis

A1 achieves 56.7x speedup in test-time scaling and 4.14x improvement in throughput compared to target model-only scaling, with no loss in accuracy. The framework maintains accurate rejection-rate control, reduces latency and memory overhead, and matches the performance of the target model across diverse reasoning benchmarks (MATH, AMC23, AIME24, AIME25).

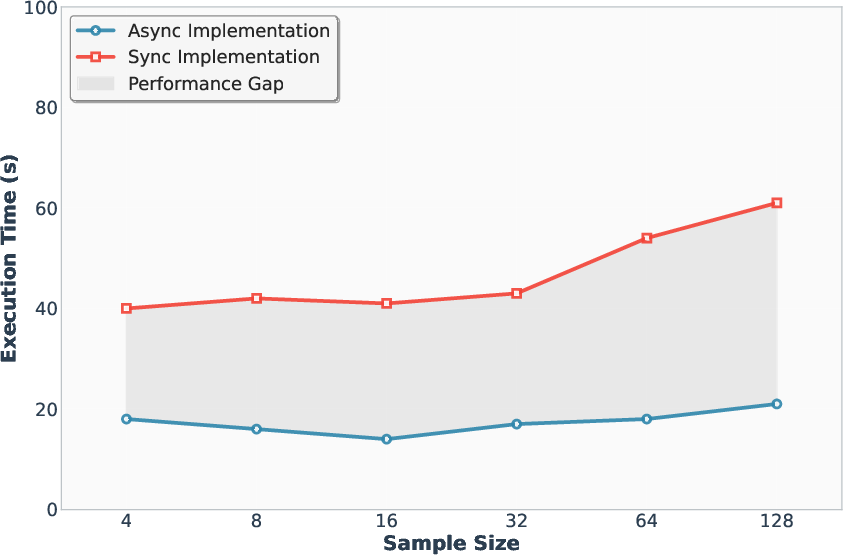
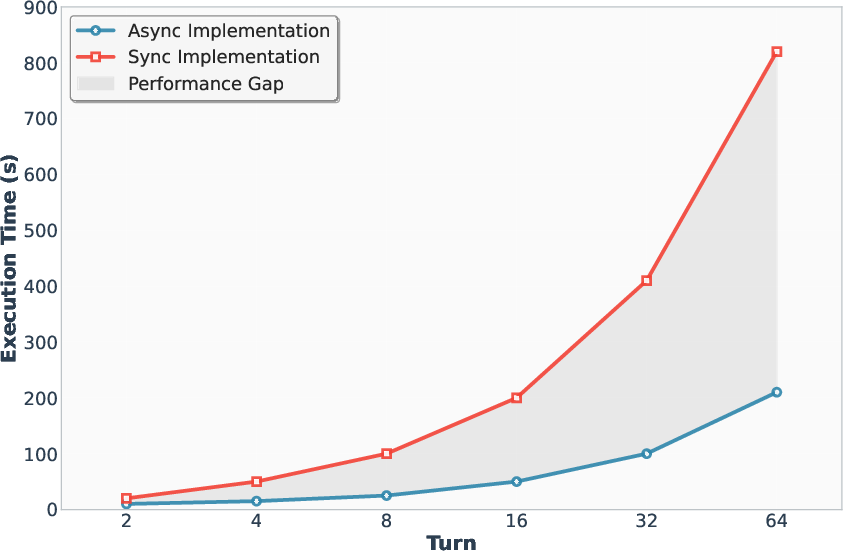
Figure 4: Sampling latency, demonstrating the efficiency gains of A1 over synchronous speculative decoding.

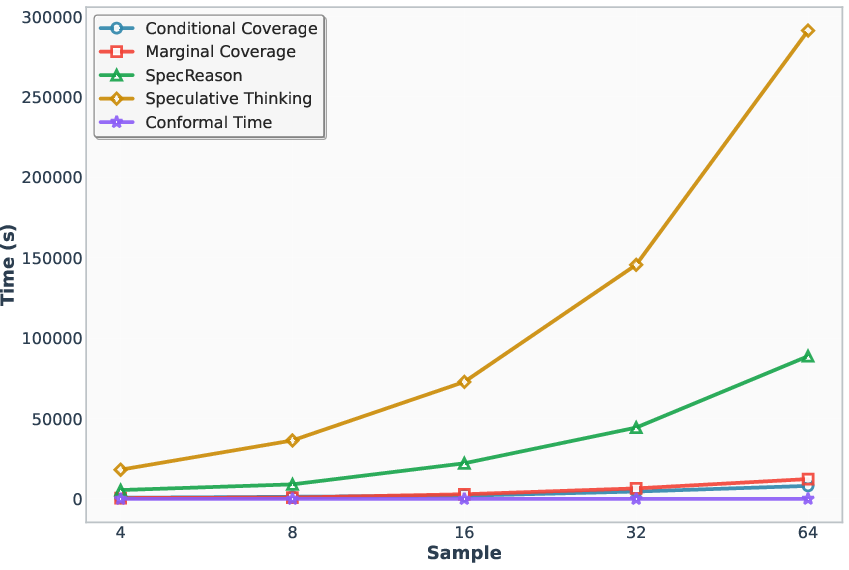
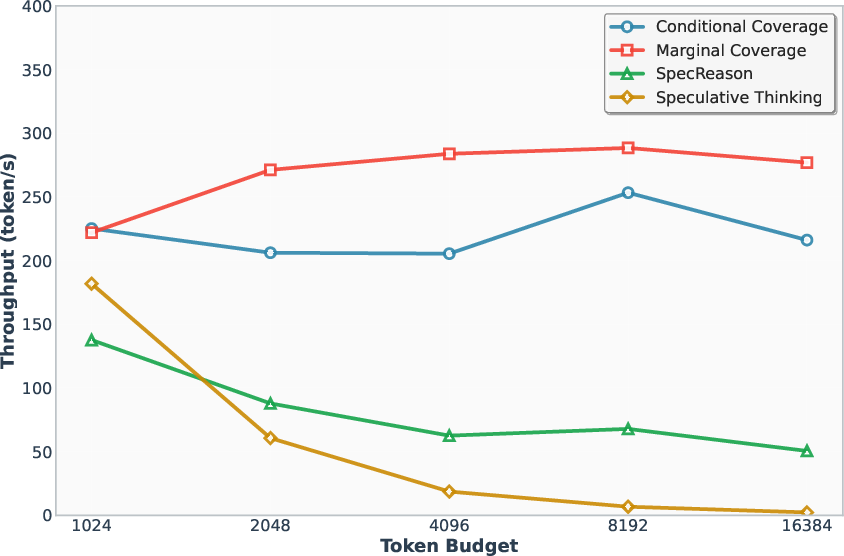
Figure 5: Latency increases with the number of samples, highlighting the scalability of A1 in high-concurrency settings.

Budget prediction accuracy is high, with absolute error within 2–5% under both marginal and conditional coverage, especially when calibration and sampling token budgets are matched and the number of parallel samples is increased.

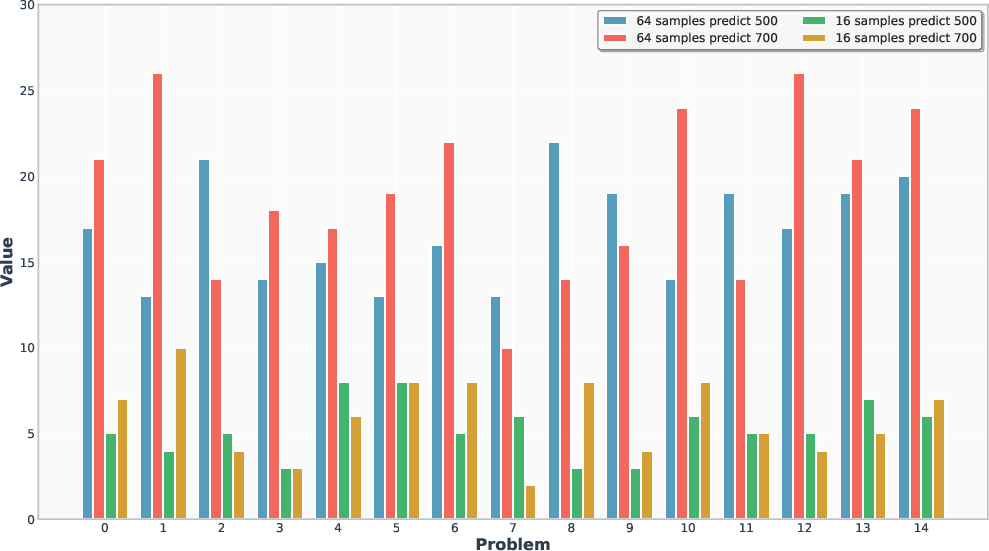
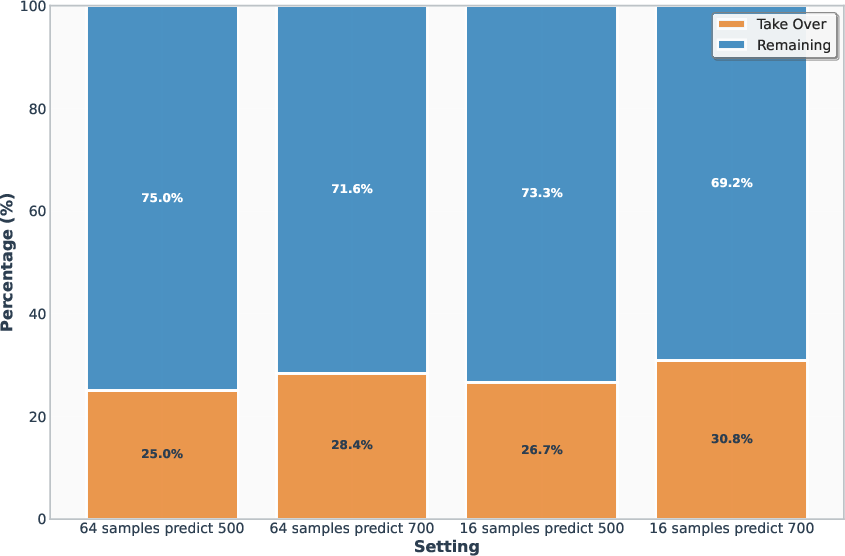
Figure 6: Left: Conditional Coverage, showing precise per-batch budget control and coverage guarantees.

A1 also demonstrates significant reductions in token consumption, particularly under conditional coverage, due to instance-level budget prediction.

Theoretical Guarantees

The paper provides rigorous proofs of marginal and conditional coverage for the conformal prediction-based rejection sampling procedure. Under exchangeability assumptions, the prediction set constructed by A1 satisfies $\mathbb{P}(y \in C_\alpha(Y)) \geq 1 - \alpha$ for both marginal and conditional settings. The framework also supports simultaneous coverage guarantees across the entire test dataset.

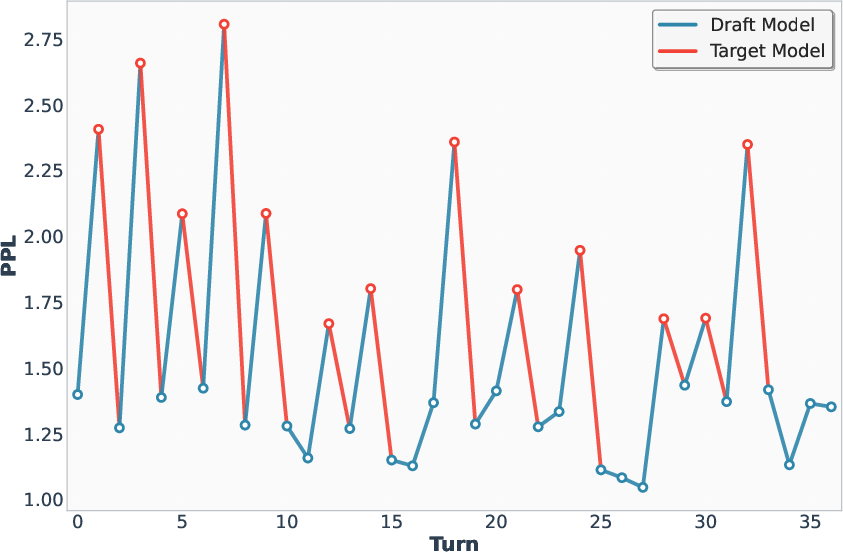
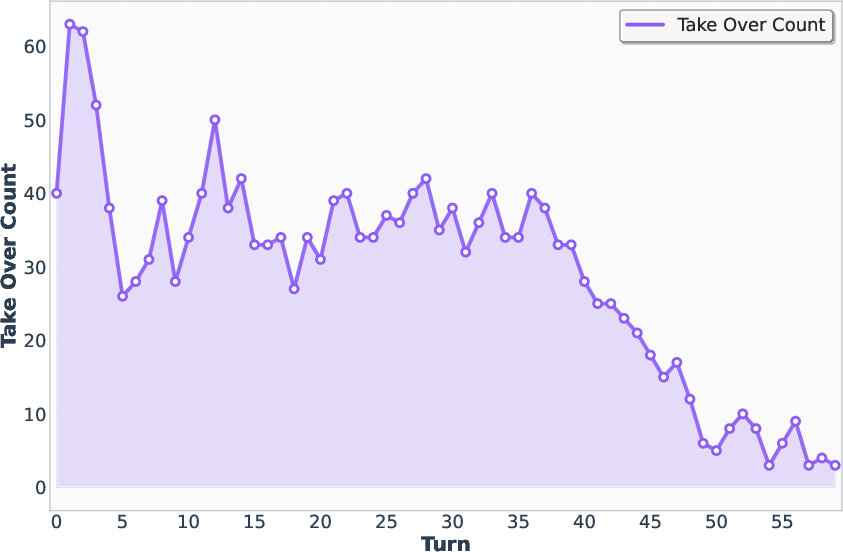
Figure 7: PPL variation with increasing turns, illustrating the effect of target model intervention on perplexity and rejection rate.

Implications and Future Directions

A1 establishes a principled approach for scalable LLM inference, enabling efficient deployment of reasoning models in high-throughput, resource-constrained environments. The integration of conformal prediction for adaptive rejection sampling provides statistical guarantees and fine-grained control over resource allocation. The framework is agnostic to model families and supports both reasoning and non-reasoning models.

Potential future developments include dynamic adaptation of rejection rates, integration with event-driven scheduling architectures, and extension to multi-agent or tool-calling scenarios. The theoretical foundation of asynchronous arithmetic intensity and conformal prediction may inform new directions in compute-optimal inference and uncertainty quantification for LLMs.

Conclusion

A1 introduces asynchronous test-time scaling via conformal prediction, addressing the synchronization and memory bottlenecks inherent in parallel speculative decoding. By refining system metrics and leveraging adaptive, statistically guaranteed rejection sampling, A1 achieves substantial efficiency gains without compromising accuracy. The framework is well-suited for scalable LLM deployment and provides a foundation for further research in adaptive inference and resource-aware reasoning.