Computational complexity of Berry phase estimation in topological phases of matter (2509.13423v1)

Abstract: The Berry phase is a fundamental quantity in the classification of topological phases of matter. In this paper, we present a new quantum algorithm and several complexity-theoretical results for the Berry phase estimation (BPE) problems. Our new quantum algorithm achieves BPE in a more general setting than previously known quantum algorithms, with a theoretical guarantee. For the complexity-theoretic results, we consider three cases. First, we prove $\mathsf{BQP}$-completeness when we are given a guiding state that has a large overlap with the ground state. This result establishes an exponential quantum speedup for estimating the Berry phase. Second, we prove $\mathsf{dUQMA}$-completeness when we have \textit{a priori} bound for ground state energy. Here, $\mathsf{dUQMA}$ is a variant of the unique witness version of $\mathsf{QMA}$ (i.e., $\mathsf{UQMA}$), which we introduce in this paper, and this class precisely captures the complexity of BPE without the known guiding state. Remarkably, this problem turned out to be the first natural problem contained in both $\mathsf{UQMA}$ and $\mathsf{co}$-$\mathsf{UQMA}$. Third, we show $\mathsf{P}^{\mathsf{dUQMA[log]}}$-hardness and containment in $\mathsf{P}^{\mathsf{PGQMA[log]}}$ when we have no additional assumption. These results advance the role of quantum computing in the study of topological phases of matter and provide a pathway for clarifying the connection between topological phases of matter and computational complexity.

• The paper presents a novel quantum algorithm using dual adiabatic evolutions to isolate the Berry phase.
• The paper establishes BQP-completeness and introduces the dUQMA complexity class for energy-threshold analysis.
• The paper’s results imply efficient classification of topological phases with robust quantum advantages for practical quantum computing.

Computational Complexity of Berry Phase Estimation in Topological Phases of Matter

Introduction and Motivation

The Berry phase is a central topological invariant in the classification of topological phases of matter, with profound implications for condensed matter physics and quantum information. Estimating the Berry phase in quantum many-body systems is computationally challenging, especially in the presence of strong correlations and large system sizes. This paper rigorously investigates the computational complexity of Berry phase estimation (BPE), introducing new quantum algorithms and establishing complexity-theoretic results that clarify the quantum advantage and limitations in this domain.

Figure 1: The paper studies the quantum computational complexity of Berry phase estimation and its realization on quantum computers.

Problem Formulation

The Berry phase estimation problem is defined for families of $k$-local $n$-qubit Hamiltonians $\{H(\lambda)\}_{\lambda \in [0,1]}$ with non-degenerate ground states and inverse-polynomial spectral gap. The task is to decide, under a promise, whether the Berry phase $\theta_B$ lies in one of two separated intervals in $[0,2\pi)$, given parameters $a, b, \delta$.

Three variants are considered:

1. BPE with Known Guiding State: A succinct description of a state with large overlap with the ground state is provided.
2. BPE with Energy Threshold: An a priori bound for the ground state energy is given, separating it from the first excited state.
3. BPE without Additional Inputs: No guiding state or energy threshold is provided.

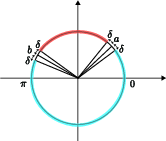
   Figure 2: The Berry phase estimation problem reduces to deciding whether $\theta_B$ is in the red or blue region for given $a, b$.

Quantum Algorithm for Berry Phase Estimation

The paper introduces a quantum algorithm that generalizes previous approaches and removes symmetry restrictions, enabling estimation of $\theta_B$ modulo $2\pi$ with inverse-polynomial precision. The key innovation is the use of two adiabatic evolutions with different runtimes, exploiting the invariance of the Berry phase and the scaling of the dynamical phase. Quantum phase estimation (QPE) is applied to both evolutions, and post-processing cancels the dynamical phase, isolating $\theta_B$.

Algorithmic Steps

• Ground State Preparation: Using a guiding state with inverse-polynomial overlap, efficient ground state preparation is achieved via polynomial filtering and block-encoding techniques.
• Adiabatic Evolution: Two evolutions are performed with runtimes $T$ and $\alpha T$, where $\alpha > 1$.
• Phase Estimation: QPE yields estimates of $\theta_B + \theta_D$ and $\theta_B + \alpha \theta_D$.
• Algebraic Reconstruction: The Berry phase is recovered by combining the two estimates, unwrapping the dynamical phase contribution.

This algorithm achieves polynomial runtime in $n$, $1/\varepsilon_B$, and $\log(1/\eta)$, where $\varepsilon_B$ is the target precision and $\eta$ the failure probability.

Complexity-Theoretic Results

BQP-Completeness

• BPE with Guiding State: The problem is shown to be BQP-complete. Given a guiding state, the Berry phase can be estimated efficiently on a quantum computer, and the problem is as hard as any in BQP. The reduction uses a circuit-to-Hamiltonian construction, encoding the outcome of a quantum computation in the Berry phase intervals.

dUQMA-Completeness

• BPE with Energy Threshold: The paper introduces the doubly Unique QMA (dUQMA) complexity class, capturing problems with unique witnesses for both YES and NO instances. BPE with energy threshold is dUQMA-complete, and is the first natural problem contained in both UQMA and co-UQMA. The reduction leverages a penalty term in the Hamiltonian to enforce uniqueness and spectral gap conditions.

Hardness and Containment

• BPE without Additional Inputs: The problem is $\mathsf{P}^{\mathsf{dUQMA[log]}$-hard under polynomial-time truth-table reductions and contained in $\mathsf{P}^{\mathsf{PGQMA[log]}$. The reduction uses binary search over ground state energies and queries to PGQMA oracles.

Technical Innovations

• Generalization of Previous Algorithms: The new quantum algorithm overcomes the $[0,\pi)$ restriction of prior work (Murta et al.), enabling full-range Berry phase estimation without time-reversal symmetry.
• Complexity Class dUQMA: The introduction and characterization of dUQMA provides a refined framework for problems with unique witnesses in both decision outcomes, with amplification theorems ensuring exponentially small error without increasing witness length.
• Circuit-to-Hamiltonian Reductions: The constructions encode computational outcomes in Berry phase intervals, leveraging perturbation theory and spectral gap analysis.

Implications and Future Directions

The results establish a rigorous quantum advantage for Berry phase estimation in topological phases, with BQP-completeness in the presence of a guiding state. The identification of dUQMA-completeness for the energy threshold variant opens new avenues for the paper of unique witness quantum complexity classes. The containment and hardness results for the general BPE problem suggest that further progress may require new algorithmic or complexity-theoretic techniques.

Practical implications include the potential for quantum computers to efficiently classify topological phases via Berry phase estimation, with robustness against local noise due to the topological nature of the invariants. Theoretical implications extend to the complexity of other topological invariants (e.g., Chern numbers), quantum-inspired classical algorithms for constant precision, and reductions to physically motivated Hamiltonians.

Open questions include:

• Complexity of estimating other topological invariants (Chern number, degenerate eigenvectors).
• Classical containment for Berry phase estimation at constant precision.
• Extension of hardness results to more physical Hamiltonians.
• Further characterization and separation of related complexity classes (UQMA, DUQMA).

Conclusion

This work provides a comprehensive complexity-theoretic and algorithmic analysis of Berry phase estimation in topological phases of matter. The results clarify the quantum advantage, introduce new complexity classes, and establish rigorous reductions, setting the stage for future research in quantum computational complexity and the classification of topological phases. The technical innovations in quantum algorithms and complexity theory have broad implications for both theoretical and practical quantum computing.