- The paper develops a continuous-time principal-agent model for shared order books and rigorously derives equilibrium conditions for optimal incentive contracts.
- It employs BSDEs and dynamic programming to obtain semi-explicit forms for bid-ask spreads and contract parameters under stochastic order flows.
- The study demonstrates that incentive provision acts as a public good, yielding substantial liquidity gains while provoking free-rider challenges in competitive markets.
Competition and Incentives in a Shared Order Book: Principal-Agent Dynamics and Public Good Effects
Introduction and Motivation
The paper develops a continuous-time Principal-Agent model to analyze the strategic interactions between two exchanges sharing a single limit order book (SLOB), with each exchange employing a dedicated market maker. This framework is motivated by recent regulatory changes in European intraday electricity markets, notably Regulation (EU) 2019/943, which mandates the possibility of shared order books to foster competition and liquidity. The model is also relevant to decentralized finance (DeFi) environments, where aggregators connect multiple venues, and to analogous settings in other industries.
A key feature of the SLOB mechanism is that a quote posted by a market maker on one exchange can be executed by a market order arriving on another exchange. This interconnection introduces complex strategic incentives: exchanges may be tempted to free-ride on the liquidity provision efforts of competitors, potentially leading to suboptimal market outcomes.
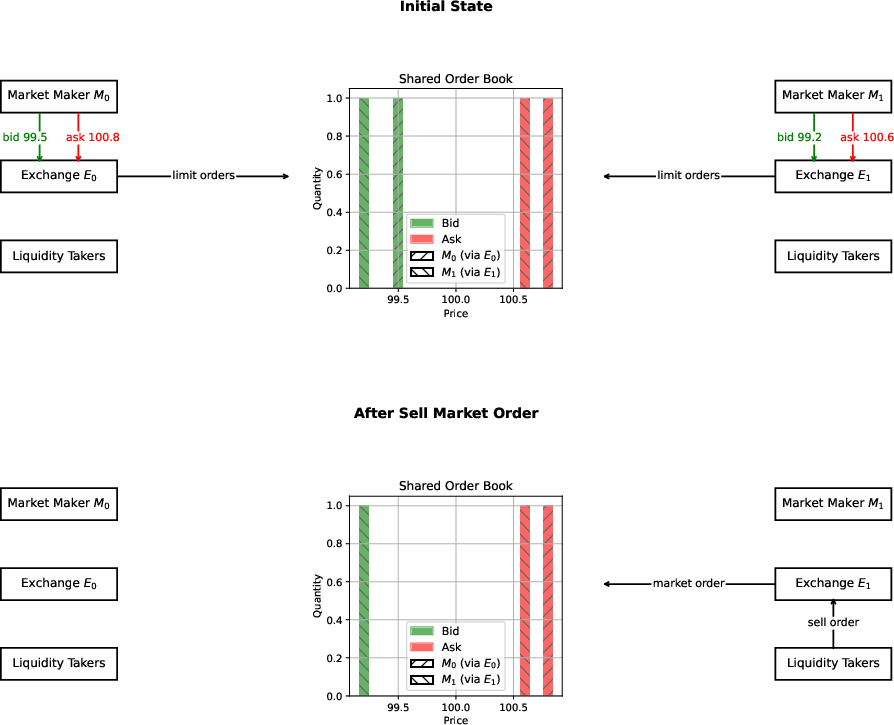
Figure 1: Mechanism of a shared limit order book, illustrating cross-exchange liquidity provision and consumption.
The model considers two exchanges (E0, E1), each with a market maker (M0, M1), operating over a finite horizon T for a single asset whose fundamental price follows an arithmetic Brownian motion. Market makers quote bid and ask prices, controlling the spread and thus the rate of order arrivals, which are modeled as Poisson processes with exponential intensity functions dependent on the quoted spreads.
Each exchange acts as a Principal, offering incentive contracts to its market maker (Agent). All agents have CARA utility functions, with potentially heterogeneous risk aversion parameters. The incentive contracts are indexed on order arrivals and the asset price, and the exchanges' objective functions incorporate both transaction revenues and the cost of incentives.
The model introduces a parameter β to capture the efficiency of the connection between exchanges. When β=1, the SLOB is fully efficient: market makers never receive more than the best quote. When β=0, market makers can benefit from less competitive quotes.
Nash Equilibrium and Contract Characterization
The paper rigorously establishes the existence and uniqueness of Nash equilibria between exchanges, characterizes the optimal incentive contracts, and provides a numerical solution to the associated PDEs for the certainty equivalents of the exchanges. The equilibrium analysis is performed in three regimes:
- No Incentives: Both exchanges abstain from offering contracts.
- Unilateral Incentives: Only one exchange provides an incentive contract.
- Bilateral Incentives: Both exchanges offer contracts to their respective market makers.
The equilibrium bid-ask spreads are derived as fixed points of the market makers' Hamiltonians, with explicit dependence on the incentive rates and inventory positions. The contract representation leverages backward stochastic differential equations (BSDEs) and dynamic programming principles, yielding semi-explicit forms for the optimal contracts.
Economic Implications: Public Good and Free-Rider Effects
A central economic result is that incentive provision in the SLOB context constitutes a public good. When one exchange incentivizes its market maker, the resulting tighter spreads and increased liquidity benefit both exchanges due to the shared nature of the order book. This creates a competitiveness spillover: the passive exchange reaps indirect benefits without incurring the cost of incentive provision.
Numerical results demonstrate that the unilateral provision of incentives by one exchange substantially increases the utility of both exchanges, while the incremental benefit of bilateral incentives is marginal. This is illustrated in the value functions of the exchanges as a function of inventory and risk aversion parameters.
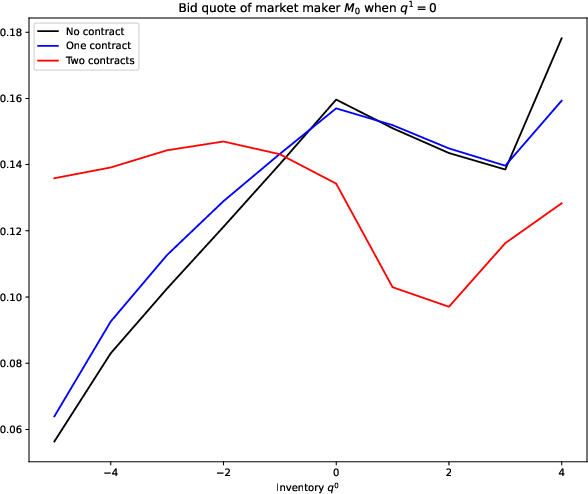

Figure 2: Optimal bid quote of the market makers as a function of the inventory of market maker M0 (left) and M1 (right).
The spillover effect induces a free-rider problem: since incentive provision is costly, both exchanges have an incentive to let the other bear the cost, potentially resulting in an equilibrium with no incentives and diminished overall competition and liquidity.
Numerical Analysis and Policy Implications
The model is calibrated to realistic parameter values for intraday electricity markets. Explicit Euler schemes are used to solve the system of PDEs governing the exchanges' value functions and the market makers' optimal quotes.
Key findings include:
- Liquidity Gains: The introduction of a single incentive contract leads to a significant reduction in bid-ask spreads and increased liquidity, with most of the benefit accruing from the first mover.
- Marginal Returns: The second incentive contract yields only a small additional improvement in liquidity and exchange utility.
- Inventory Dynamics: Market makers adjust their quotes dynamically in response to inventory positions and the presence of incentives, with competitive pressure forcing alignment of quotes even in the absence of direct incentives.
These results have direct implications for market design and regulation. The identification of incentive provision as a public good suggests that regulatory mandates for SLOBs should be accompanied by mechanisms to mitigate free-rider problems, such as coordinated incentive schemes or cost-sharing arrangements.
Theoretical and Practical Extensions
The theoretical framework is generalizable to other multi-agent market settings, including DeFi aggregators and multi-venue financial markets. The use of CARA utilities, Poisson order arrivals, and BSDE-based contract representation provides a tractable yet flexible foundation for further research.
Potential extensions include:
- Heterogeneous Agents: Allowing for more complex agent heterogeneity in risk aversion, inventory constraints, and order flow sensitivity.
- Dynamic Contracting: Incorporating adaptive or renegotiable contracts in response to market conditions.
- Multi-Asset and Multi-Exchange Generalization: Extending the model to multiple assets and more than two exchanges, with network effects.
Conclusion
The paper provides a rigorous analysis of competition and incentives in shared order book environments, demonstrating that incentive provision is a public good subject to free-rider problems. The model offers actionable insights for market operators and regulators, highlighting the need for coordinated approaches to liquidity provision in interconnected markets. The mathematical and economic results are robust and broadly applicable, with clear implications for the design of efficient, competitive trading platforms.




