Conditioning on PDE Parameters to Generalise Deep Learning Emulation of Stochastic and Chaotic Dynamics (2509.09599v1)

Abstract: We present a deep learning emulator for stochastic and chaotic spatio-temporal systems, explicitly conditioned on the parameter values of the underlying partial differential equations (PDEs). Our approach involves pre-training the model on a single parameter domain, followed by fine-tuning on a smaller, yet diverse dataset, enabling generalisation across a broad range of parameter values. By incorporating local attention mechanisms, the network is capable of handling varying domain sizes and resolutions. This enables computationally efficient pre-training on smaller domains while requiring only a small additional dataset to learn how to generalise to larger domain sizes. We demonstrate the model's capabilities on the chaotic Kuramoto-Sivashinsky equation and stochastically-forced beta-plane turbulence, showcasing its ability to capture phenomena at interpolated parameter values. The emulator provides significant computational speed-ups over conventional numerical integration, facilitating efficient exploration of parameter space, while a probabilistic variant of the emulator provides uncertainty quantification, allowing for the statistical study of rare events.

• The paper introduces a transformer architecture conditioned on PDE parameters to generalize across stochastic and chaotic dynamics.
• It leverages local attention and adaptive layer normalization to capture multi-scale effects while reducing computational complexity.
• Demonstrated through Kuramoto-Sivashinsky and beta-plane turbulence cases, the method achieves accurate long-term forecasting and uncertainty quantification.

Conditioning on PDE Parameters to Generalise Deep Learning Emulation of Stochastic and Chaotic Dynamics

Introduction

The paper presents a novel deep learning framework designed to emulate stochastic and chaotic spatiotemporal systems conditionally based on parameters of the underlying PDEs. The methodology involves pre-training a neural network model on data from a single parameter domain, followed by fine-tuning it on a diverse dataset. The architecture leverages a transformer-based neural network model modified with local attention mechanisms and adaptive layer normalization to handle different domain sizes and resolutions, offering significant computational advantages over traditional numerical integration approaches.

Neural Network Architecture

The core of the approach involves a transformer architecture uniquely adapted for handling PDE-based emulation through conditioning on continuous scalar parameters ($\beta$ for the stochastic beta-plane turbulence and $L$ for the Kuramoto-Sivashinsky equation). The network incorporates an innovative mix of local attention mechanisms and adaptive layer normalization, allowing for efficient handling of varying input scales and parameter conditioning.

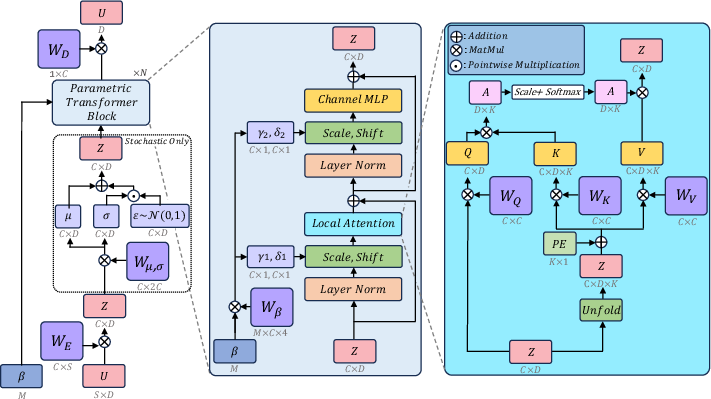
Figure 1: Schematic of the neural network architecture incorporating local attention and adaptive layer normalization, conditioned on PDE parameters.

Local Attention Mechanism

The integration of local attention mechanisms mirrors the advantages seen in CNN architectures by focusing on localized spatial interactions. This allows the model to adaptively capture multi-scale spatial correlations. The use of an unfold operation applies local attention efficiently, reducing computational complexity significantly from $D^2$ to $D \times K$, where $D$ is the domain size and $K$ is the attention window.

Generalization through Parametric Conditioning

The model achieves generalization by training with adaptive layer normalization, conditioned on PDE parameters without relying on transformations. This conditioning occurs through learned varying affine transformations applied to the attention and MLP layers within each transformer block.

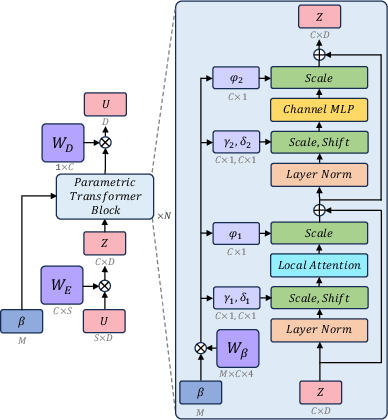
Figure 3: Architecture conditioned on parameter $L$ using flexible dimensions within the parameter space.

Kuramoto-Sivashinsky Application

For testing, the Kuramoto-Sivashinsky (KS) equation was employed, requiring the model to capture complex chaotic dynamics across variable domain sizes $L$. The neural network, pre-trained on $L=22$ and fine-tuned on other values, demonstrated proficiency in long-term forecasting accuracy, capturing behavioral dynamics not explicitly encountered during training.

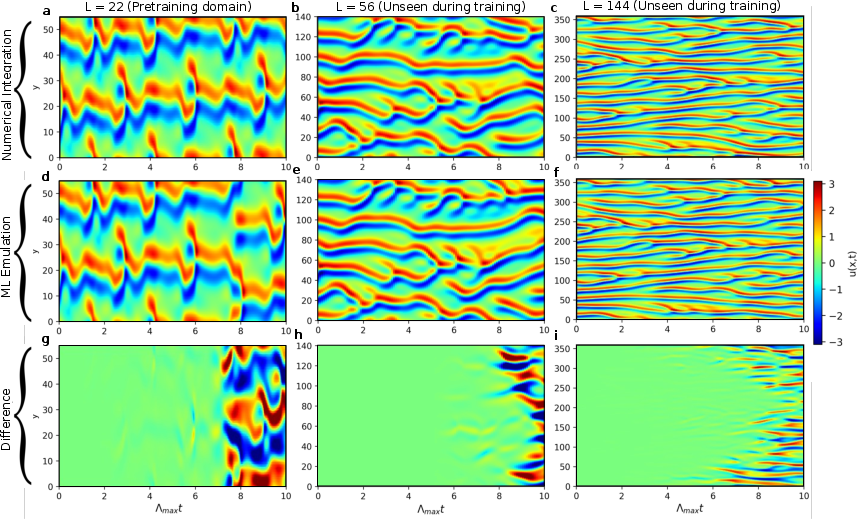
Figure 4: Space-time plots for the KS equation showcasing results from numerical integration and ML emulation across various domains.

Beta-Plane Turbulence Application

The model was further applied to simulate the complex dynamics of beta-plane turbulence. Unlike traditional simulations, this approach offers an autoregressive forecast capability utilizing a probabilistic variant trained through CRPS, enabling ensemble forecasts and quantifying uncertainties efficiently over large parameter spaces.

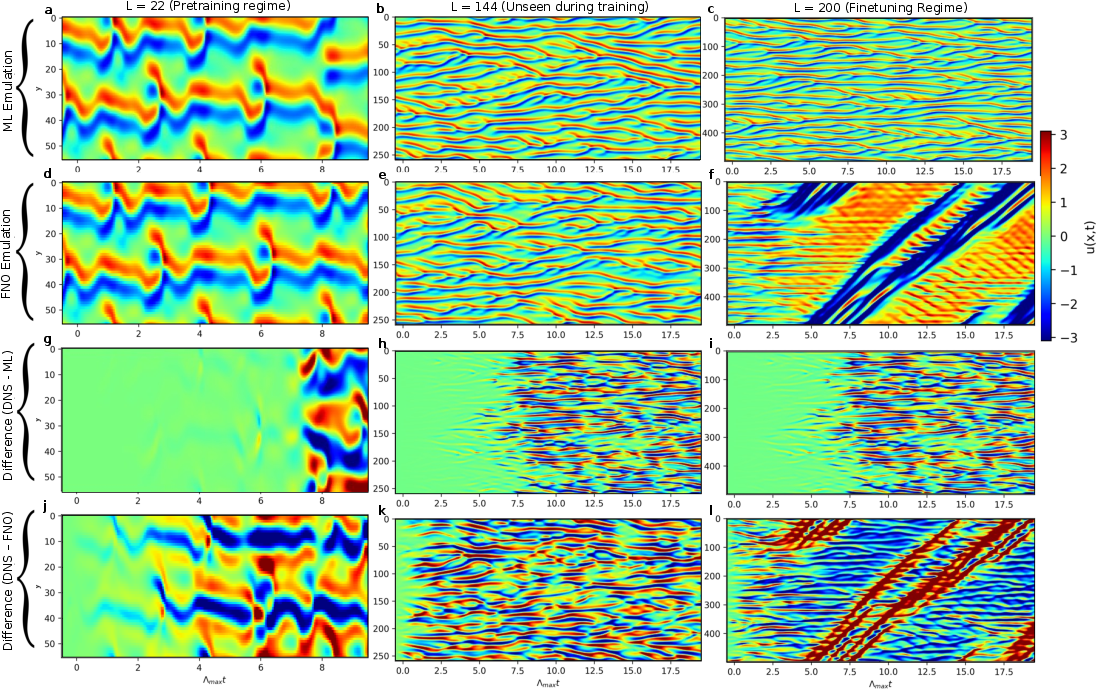
Figure 5: Latitude-time plots for zonal flow $U(y,t)$, displaying ensemble forecasts generated by both neural network and numerical simulations.

Probabilistic Modelling and Statistical Validation

Probabilistic modeling was vital for under-resolved inputs, achieved through stochastic sampling layers facilitating diverse ensemble generation. The model effectively maintained key statistical properties aligned with physically accurate simulations, including spectral energy distributions across scales and joint probability assessments for dependent variables.

Figure 6: PDFs displaying joint probabilities of $U$, $\partial_y U$, and $\partial_t U$ for the beta plane system across various states.

Conclusion

The neural network demonstrates exceptional capability in capturing the dynamics of complex PDE systems while efficiently generalizing across broad parameter spaces. Its robust adaptability extends potential applications in modeling systems where computationally exhaustive simulations might typically have been a barrier. Future considerations might involve expanding this parameter-conditioned framework to accommodate broader PDE landscapes and incorporate higher-dimensional parameter spaces for comprehensive system behavior analysis.