Echo State Networks as State-Space Models: A Systems Perspective (2509.04422v1)

Abstract: Echo State Networks (ESNs) are typically presented as efficient, readout-trained recurrent models, yet their dynamics and design are often guided by heuristics rather than first principles. We recast ESNs explicitly as state-space models (SSMs), providing a unified systems-theoretic account that links reservoir computing with classical identification and modern kernelized SSMs. First, we show that the echo-state property is an instance of input-to-state stability for a contractive nonlinear SSM and derive verifiable conditions in terms of leak, spectral scaling, and activation Lipschitz constants. Second, we develop two complementary mappings: (i) small-signal linearizations that yield locally valid LTI SSMs with interpretable poles and memory horizons; and (ii) lifted/Koopman random-feature expansions that render the ESN a linear SSM in an augmented state, enabling transfer-function and convolutional-kernel analyses. This perspective yields frequency-domain characterizations of memory spectra and clarifies when ESNs emulate structured SSM kernels. Third, we cast teacher forcing as state estimation and propose Kalman/EKF-assisted readout learning, together with EM for hyperparameters (leak, spectral radius, process/measurement noise) and a hybrid subspace procedure for spectral shaping under contraction constraints.

• The paper reexamines Echo State Networks by framing them as nonlinear discrete-time state-space models, enhancing their theoretical foundation through input-to-state stability and contraction mapping analysis.
• It employs canonical forms including small-signal linearization and Koopman expansions to reveal dynamics such as memory spectra and stability conditions critical for sequence modeling.
• The study highlights improved hyperparameter estimation via state estimation methods like Kalman filtering, paving the way for structured kernel designs and spatiotemporal applications.

Echo State Networks as State-Space Models: A Systems Perspective

The paper "Echo State Networks as State-Space Models: A Systems Perspective" re-examines Echo State Networks (ESNs), framing them within the language and analytical tools of state-space models (SSMs). This approach aims to solidify the theoretical foundation of ESNs, allowing for more rigorous analysis and fruitful application in sequence modeling tasks.

ESNs Recast as State-Space Models

ESNs are typically known for their fixed recurrent architecture with trainable linear readouts, offering efficient sequence modeling with limited computational load. However, their design often relies on heuristics like the Echo State Property (ESP) and spectral norms. This paper articulates ESNs as nonlinear discrete-time SSMs, with an emphasis on input-to-state stability (ISS), which strengthens ESP assertions. The ESN update is modeled as: $$x_{t+1} = (1-\lambda)x_t + \lambda \sigma(Wx_t + Uu_t + b) + \omega_t,\quad y_t = Cx_t + \nu_t$$ By doing so, the ESN integrates into the well-developed framework of systems theory, enabling the use of tools like Lyapunov functions for fading memory analysis.

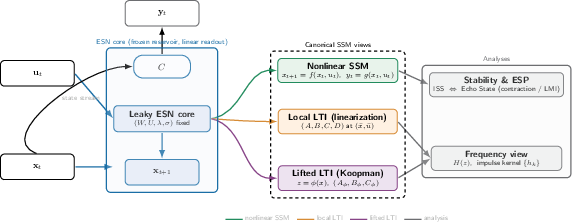
Figure 1: ESNs as SSMs: canonical views and analyses.

Analytical Canonical Forms

The paper explores various canonical mappings of ESNs:

1. Nonlinear SSMs: The ESN itself is seen as a contraction mapping, wherein conditions for ESP and ISS are derived based on model parameters like leak $\lambda$, spectral scaling, and activation Lipschitz constants.
2. Small-Signal Linearization: Around regions of operation, ESNs can be approximated by locally valid LTI models, exposing poles and memory horizons, important for understanding the dynamics and frequency responses.
3. Lifted/Koopman Expansions: Use random feature expansions to treat the ESN as a linear SSM in augmented state space, facilitating transfer-function analysis and structured convolutional kernels.

Teacher Forcing and State Estimation

The framework of teacher forcing in training ESNs is likened to state estimation, proposing the use of Kalman and Extended Kalman Filters (EKF) to improve readout learning. This perspective allows for principled estimation of hyperparameters, including the leak factor, spectral radius, and noise levels, employing techniques like Expectation-Maximization (EM).

Frequency-Domain Analysis

The frequency-domain characterization of memory spectra in ESNs is expanded, revealing when ESNs emulate modern SSM kernels through structured transfer functions. This view clarifies how ESNs manage memory and how they can be tuned effectively to match desired sequence characteristics.

Implications and Future Developments

The paper's systems-theoretic reframing of ESNs not only enhances understanding but also points toward avenues for advanced applications in AI:

• Structured Kernel Designs: Offers a basis for designing state-space models that can handle long-context learning more effectively.
• Probabilistic Extensions: Implicates the use of stochastic models to enhance robustness and predictive accuracy in uncertain scenarios.
• Spatiotemporal Applications: Proposes convolutional ESN designs for spatiotemporal data, aligning with modern machine learning trends.

Conclusion

By situating ESNs firmly within the field of state-space models, the paper lays a robust analytical foundation for leveraging systems theory in ground-truthing and expanding reservoir computing paradigms. It facilitates systematic stability and identification procedures, making ESN designs more transparent and effective for a range of applications. The exploration into structured kernels and frequency-domain analyses situates ESNs as viable candidates for tasks dominated by long-range dependencies.