Transition Models: Rethinking the Generative Learning Objective (2509.04394v1)

Abstract: A fundamental dilemma in generative modeling persists: iterative diffusion models achieve outstanding fidelity, but at a significant computational cost, while efficient few-step alternatives are constrained by a hard quality ceiling. This conflict between generation steps and output quality arises from restrictive training objectives that focus exclusively on either infinitesimal dynamics (PF-ODEs) or direct endpoint prediction. We address this challenge by introducing an exact, continuous-time dynamics equation that analytically defines state transitions across any finite time interval. This leads to a novel generative paradigm, Transition Models (TiM), which adapt to arbitrary-step transitions, seamlessly traversing the generative trajectory from single leaps to fine-grained refinement with more steps. Despite having only 865M parameters, TiM achieves state-of-the-art performance, surpassing leading models such as SD3.5 (8B parameters) and FLUX.1 (12B parameters) across all evaluated step counts. Importantly, unlike previous few-step generators, TiM demonstrates monotonic quality improvement as the sampling budget increases. Additionally, when employing our native-resolution strategy, TiM delivers exceptional fidelity at resolutions up to 4096x4096.

• The paper introduces a novel generative learning objective via Transition Models (TiM) that learns arbitrary state-to-state transitions.
• It employs decoupled time and interval embeddings with interval-aware attention to enhance both global restructuring and local refinement.
• Empirical results show TiM outperforms multi-billion parameter models in efficiency and fidelity across diverse resolutions and aspect ratios.

Transition Models: Rethinking the Generative Learning Objective

Motivation and Theoretical Foundations

The paper introduces Transition Models (TiM), a new generative modeling paradigm that addresses the persistent trade-off between fidelity and efficiency in diffusion-based image synthesis. Traditional diffusion models achieve high sample quality via iterative denoising, but incur substantial computational cost due to large numbers of function evaluations (NFEs). Few-step alternatives, such as consistency models and distillation-based approaches, offer efficiency but suffer from a hard quality ceiling and lack monotonic improvement with increased sampling steps. The authors identify the root cause as the granularity of the learning objective: local PF-ODE supervision enables fine-grained refinement but is only accurate for infinitesimal steps, while endpoint supervision (few-step models) lacks compositionality and saturates early.

TiM is formulated by analytically deriving a continuous-time state transition identity that governs the evolution of the generative process over arbitrary intervals $\Delta t$. Rather than approximating local dynamics or fixed endpoints, TiM learns the entire solution manifold of the generative trajectory, parameterizing transitions between any state $\mathbf{x}_t$ and a previous state $\mathbf{x}_{t-\Delta t}$ for arbitrary $\Delta t$. This unifies the few-step and many-step regimes, enabling a single model to operate efficiently and with high fidelity across the full spectrum of sampling budgets.

Figure 1: TiM learns arbitrary state-to-state transitions, unifying local vector field modeling and endpoint mapping within a single generative framework.

Model Architecture and Training

TiM builds upon a transformer-based backbone (DiT), introducing two key architectural innovations:

• Decoupled Time and Interval Embeddings: Separate encoders for absolute time $t$ and transition interval $\Delta t$ allow the model to distinguish between current state and transition magnitude, improving temporal reasoning and compositionality.
• Interval-Aware Attention: The transition interval embedding is injected into the query, key, and value projections of self-attention, enabling the model to adapt spatial dependencies to the scale of the transition (global restructuring for large $\Delta t$, local refinement for small $\Delta t$).

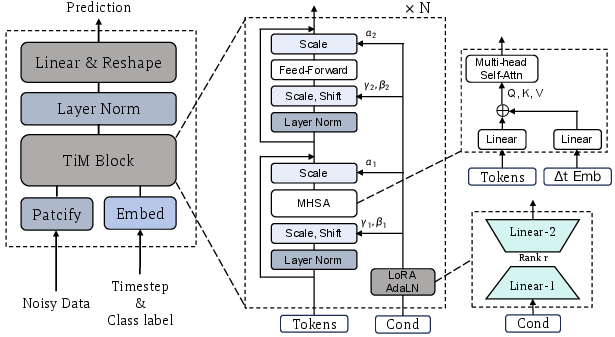
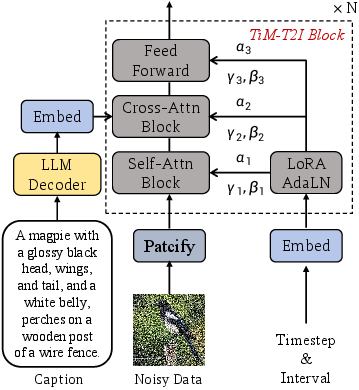
Figure 2: TiM model architecture, highlighting decoupled time/interval embeddings and interval-aware attention mechanisms.

The training objective is derived from the state transition identity, enforcing both path consistency (compositionality of transitions) and time-slope matching (higher-order supervision on the temporal derivative of the residual). To scale training to large models, the authors replace Jacobian-vector product (JVP) computation with a forward-pass-only finite-difference approximation (Differential Derivation Equation, DDE), which is compatible with FSDP and FlashAttention. A loss weighting scheme prioritizes short-interval transitions to stabilize gradients.

Empirical Results

TiM is validated on text-to-image and class-guided image generation benchmarks, including GenEval, MJHQ30K, and DPGBench. The 865M parameter TiM model, trained from scratch, consistently outperforms multi-billion parameter baselines (SD3.5-Large, FLUX.1-Dev) across all NFEs, resolutions, and aspect ratios.

• GenEval: TiM achieves a score of 0.67 at 1-NFE and 0.83 at 128-NFE, surpassing SD3.5-Large (8B) and FLUX.1-Dev (12B) at all step counts. Unlike few-step distilled models, TiM exhibits monotonic quality improvement as NFE increases.
• Resolution and Aspect Ratio Generalization: TiM reliably generates images up to $4096\times4096$ and handles extreme aspect ratios (e.g., $1024\times4096$, $2560\times1024$), outperforming all baselines in both fidelity and text alignment.

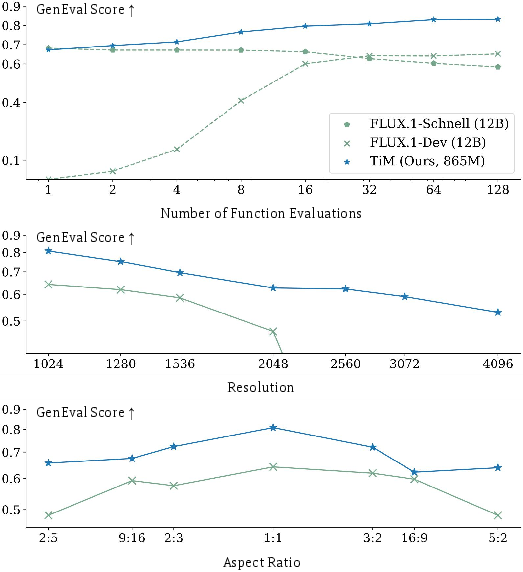
  Figure 3: TiM's superior performance across NFEs, resolutions, and aspect ratios on GenEval.

  

  Figure 4: High-resolution and multi-aspect generations from TiM (128 NFEs), demonstrating robust scaling and generalization.

Qualitative analysis reveals that TiM maintains high fidelity and prompt alignment across all NFEs, whereas multi-step diffusion models collapse at low NFEs and few-step distilled models produce over-saturated outputs at high NFEs.

Figure 5: TiM delivers superior fidelity and text alignment across all NFEs, avoiding the step–quality trade-offs of prior methods.

Ablation and Implementation Analysis

Ablation studies confirm the necessity of each component:

• Transition objective (vs. standard diffusion) yields >6× improvement in few-step FID.
• Decoupled time embedding and interval-aware attention are complementary, each providing substantial gains.
• DDE enables scalable training without sacrificing performance.
• Time weighting and mixed timestep sampling further refine stability and convergence.

TiM is trained from scratch on 33M images for 30 days using 16 A100 GPUs, with native-resolution strategies and resolution-dependent timestep shifting. The model supports arbitrary-step sampling, including stochastic variants for diversity.

Implications and Future Directions

TiM demonstrates that the trade-off between efficiency and fidelity in generative modeling is not architectural but objective-driven. By learning the solution manifold of the generative process, TiM achieves strong few-step performance, monotonic refinement, and robust scaling to high resolutions and aspect ratios—all within a compact model. This paradigm shift has several implications:

• Foundation Model Efficiency: TiM's ability to outperform much larger models suggests that future foundation models can be both efficient and high-performing, reducing hardware requirements and democratizing access.
• Unified Generative Frameworks: The transition-based objective unifies local and global supervision, potentially generalizing to other modalities (video, 3D, multimodal synthesis) and tasks (inpainting, editing).
• Sampling Flexibility: Arbitrary-step and schedule-agnostic sampling enables adaptive inference, trading off speed and quality dynamically.
• Theoretical Generalization: The state transition identity provides a principled framework for compositionality and trajectory consistency, which may inform future work in flow-based, consistency, and shortcut models.

Limitations remain in content safety, controllability, and fine-grained detail rendering (e.g., text, hands), with occasional artifacts at extreme resolutions. Addressing these will require further advances in autoencoder design and training data curation.

Conclusion

Transition Models (TiM) redefine the generative learning objective, enabling a single model to master arbitrary state-to-state transitions along the PF-ODE trajectory. This approach unifies the strengths of diffusion and consistency models, delivering state-of-the-art performance, efficiency, and flexibility. TiM's theoretical and empirical contributions suggest a new direction for scalable, high-fidelity generative modeling, with broad implications for the design of future foundation models and generative systems.