Thermodynamic uncertainty relation for generalized time-reversal observables (2509.01981v1)

Abstract: Time-reversal symmetry plays an essential role in the thermodynamic uncertainty relation, which bound the fluctuations of observables in terms of the associated dissipation. In fact, thermodynamic uncertainty relations are typically derived under the assumption that the observable of interest is antisymmetric under time reversal. This also suggests that existing thermodynamic uncertainty relations are restricted to a limited class of observables. In this paper, we mitigate this restriction by introducing a new class of observables that do not exhibit the exact antisymmetry but only change the sign under time reversal. We call it generalized time reversal and derive a broadly applicable thermodynamic uncertainty relation for observables with this condition. The generalization is achieved by direct statistical arguments on the probability distributions of dissipation and the observable, and holds for both deterministic and stochastic dynamics. We demonstrate the derived thermodynamic uncertainty relation in a quantum refrigeration model, showing that the precision of generalized observables remains expressible in terms of the heat-dissipation cost. The result extends the scope of thermodynamic uncertainty relations beyond what was reached by frameworks relying on strong symmetries imposed by fluctuation theorems.

• The paper derives a universal uncertainty bound for generalized time-reversal observables, relaxing the strict antisymmetry requirement to extend TUR applicability.
• The methodology leverages statistical concentration inequalities, including Cantelli's inequality, to establish a lower bound on the signal-to-noise ratio.
• The findings have practical implications for analyzing nonequilibrium systems, quantum thermal machines, and precision-dissipation trade-offs in complex dynamics.

Thermodynamic Uncertainty Relation for Generalized Time-Reversal Observables

Introduction

The thermodynamic uncertainty relation (TUR) provides a lower bound on the relative fluctuations of observables in nonequilibrium systems, typically expressed in terms of entropy production. Conventional TURs rely on the strict antisymmetry of observables under time reversal, restricting their applicability to a limited class of physical quantities, such as currents. This paper introduces a generalized TUR that relaxes the antisymmetry requirement, extending the scope to observables that merely change sign under time reversal, i.e., $\phi(\Gamma^\dagger)\phi(\Gamma)\leq0$. The derivation leverages statistical arguments and concentration inequalities, specifically Cantelli's inequality, to establish a universal lower bound on the signal-to-noise ratio for this broader class of observables.

Generalized Time-Reversal and Fluctuation Theorem Distributions

The central innovation is the definition of generalized time-reversal observables, which need not satisfy $\phi(\Gamma^\dagger) = -\phi(\Gamma)$ but only require that $\phi(\Gamma^\dagger)\phi(\Gamma)\leq0$. This minimal parity condition encompasses a wider range of physically relevant quantities, including one-sided observables and those with asymmetric magnitudes under time reversal.

The joint probability distribution $P(\sigma, \phi)$ is termed a generalized FT distribution if it satisfies:

1. $$P(\sigma, \phi) = e^{\sigma} P(-\sigma, \phi^\dagger)$$ (trajectory-level fluctuation relation),
2. $$P(\sigma, \phi) P(-\sigma, \phi^\dagger) \neq 0 \implies \phi \phi^\dagger \leq 0$$ (generalized time reversal).

This framework is compatible with both stochastic and deterministic dynamics, provided the detailed fluctuation theorem (DFT) holds.

Figure 1: Conceptual image of a generalized FT distribution, illustrating time-reversal pairs and the allocation of probability mass according to the exponential ratio.

Derivation of the Generalized TUR

The derivation proceeds by applying Cantelli's inequality to the observable $\phi$: $$\Pr(\phi \le 0) \le \frac{\mathrm{Var}[\phi]}{\mathrm{Var}[\phi] + \langle\phi\rangle^2}$$ which rearranges to a lower bound on the scaled variance: $$\frac{\mathrm{Var}[\phi]}{\langle\phi\rangle^2} \ge \frac{\Pr(\phi \le 0)}{1 - \Pr(\phi \le 0)}$$ The minimization of $\Pr(\phi \le 0)$ over all generalized FT distributions with fixed $\langle\sigma\rangle$ and $\langle\phi\rangle$ is shown to be achieved by a two-point distribution. The resulting universal TUR is: $$\frac{\mathrm{Var}[\phi]}{\langle\phi\rangle^2} \ge \frac{1}{e^{f(\langle\sigma\rangle)}}$$ where $f = x^{-1}$ is the inverse of $x(s) = s \tanh(s/2)$.

This bound is strictly looser than the conventional TUR for current-type observables: $$\frac{\mathrm{Var}[\phi]}{\langle\phi\rangle^2} \ge \frac{2}{\langle\sigma\rangle}$$ reflecting the broader applicability to observables lacking strict time-antisymmetry.

Implications and Generality

The generalized TUR accommodates observables with asymmetric magnitudes under time reversal and those vanishing in one direction, such as one-way information erasure (Landauer's principle) or positive-work observables. It is applicable to time-inhomogeneous Markov processes and systems with external perturbations, where the conventional TUR may fail.

The framework also covers cases where the observable is defined as $\phi(\Gamma) = \max\{W(\Gamma), 0\}$, capturing only positive work events. The constraint $\phi(\Gamma)\phi(\Gamma^\dagger) = 0$ is a special case of the generalized time-reversal condition.

Application: Quantum Thermal Machine

The generalized TUR is demonstrated on a three-level quantum thermal machine operating as a refrigerator, weakly coupled to three baths at different temperatures. The observable of interest is the one-sided heat extraction from the cold bath, $\phi(\Gamma) = \max\{Q_1(\Gamma), 0\}$, which does not satisfy strict time-antisymmetry.

Figure 2: Schematic diagram of a three-level quantum thermal machine, showing energy exchanges with three baths and the directionality of heat flows in the refrigerator configuration.

Numerical simulations sample the scaled variance $\mathrm{Var}[\phi]/\langle\phi\rangle^2$ as a function of mean entropy production $\langle\sigma\rangle$ for both the generalized observable $\phi$ and the standard antisymmetric observable $\phi'$. The results confirm that the generalized TUR remains valid for $\phi$, while conventional TURs are violated.

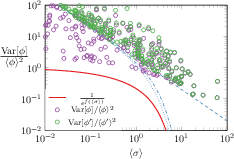
Figure 3: Simulation results for the thermal machine, comparing the scaled variance of generalized and antisymmetric observables against various TUR bounds as a function of entropy production.

Notably, the generalized TUR does not diverge in the near-equilibrium limit ($\langle\sigma\rangle \to 0$), maintaining physical interpretability where conventional bounds become uninformative.

Theoretical and Practical Implications

The generalized TUR provides a robust tool for quantifying the trade-off between precision and dissipation for a wider class of observables, including those relevant in quantum information processing, feedback control, and autonomous machines. The approach, grounded in statistical concentration inequalities, is agnostic to the underlying dynamics as long as the DFT holds, making it broadly applicable.

The relaxation of the time-reversal constraint opens avenues for analyzing systems with complex fluctuation patterns, time-dependent protocols, and observables tailored to specific operational tasks. The framework also facilitates the study of uncertainty relations in systems where only one direction of a process is physically relevant or measurable.

Conclusion

This work establishes a universal thermodynamic uncertainty relation for observables exhibiting generalized time-reversal symmetry, significantly extending the applicability of TURs beyond current-type quantities. The bound is derived via statistical arguments and concentration inequalities, and its validity is demonstrated in quantum thermal machines. The generalized TUR provides a practical and theoretically sound limit on the achievable precision of a broad class of observables, with implications for the design and analysis of nonequilibrium systems in statistical physics and quantum thermodynamics. Future research may explore further generalizations, connections to information-theoretic measures, and applications in complex driven systems.