Considerations for Estimating Causal Effects of Informatively Timed Treatments (2508.21804v1)

Abstract: Epidemiological studies are often concerned with estimating causal effects of a sequence of treatment decisions on survival outcomes. In many settings, treatment decisions do not occur at fixed, pre-specified followup times. Rather, timing varies across subjects in ways that may be informative of subsequent treatment decisions and potential outcomes. Awareness of the issue and its potential solutions is lacking in the literature, which motivate this work. Here, we formalize the issue of informative timing, problems associated with ignoring it, and show how g-methods can be used to analyze sequential treatments that are informatively timed. As we describe, in such settings, the waiting times between successive treatment decisions may be properly viewed as a time-varying confounders. Using synthetic examples, we illustrate how g-methods that do not adjust for these waiting times may be biased and how adjustment can be done in scenarios where patients may die or be censored in between treatments. We draw connections between adjustment and identification with discrete-time versus continuous-time models. Finally, we provide implementation guidance and examples using publicly available software. Our concluding message is that 1) considering timing is important for valid inference and 2) correcting for informative timing can be done with g-methods that adjust for waiting times between treatments as time-varying confounders.

• The paper demonstrates how adjusting for waiting times as time-varying confounders can significantly reduce bias in causal effect estimation.
• It compares continuous-time IPTW and discrete-time marginal structural models, showing that proper timing adjustments yield nearly unbiased estimates.
• The study provides practical implementation details and software tools, facilitating accurate causal inference in studies with irregular treatment schedules.

Estimating Causal Effects with Informatively Timed Treatments: Methodological and Practical Considerations

Introduction

This paper addresses the methodological challenges in estimating causal effects of sequential treatments when the timing of treatment decisions is informative—i.e., when the intervals between treatments are not fixed but vary across subjects in ways that are associated with both subsequent treatment choices and outcomes. The work is motivated by real-world clinical scenarios, such as pediatric acute myeloid leukemia (AML) chemotherapy regimens, where treatment initiation is contingent on patient recovery and clinical stability, and by osteoporosis management, where the duration of first-line therapy influences both the switch to second-line agents and fracture risk. The central thesis is that waiting times between treatments act as time-varying confounders, and failure to adjust for them can induce substantial bias in causal effect estimation.

Formalization of Informative Timing as Time-Varying Confounding

The paper formalizes the problem using a potential outcomes framework for $K$-stage treatment sequences, focusing on the case $K=2$ for clarity. Let $A_k$ denote the treatment at stage $k$, $L_k$ the covariates measured prior to $A_k$, and $W_k$ the waiting time between events. The directed acyclic graph (DAG) representation (Figure 2a) illustrates the confounding structure: the waiting time $W_1$ between treatments influences both the subsequent treatment $A_2$ and the survival time $W_2$, creating a backdoor path that must be blocked for valid causal inference.

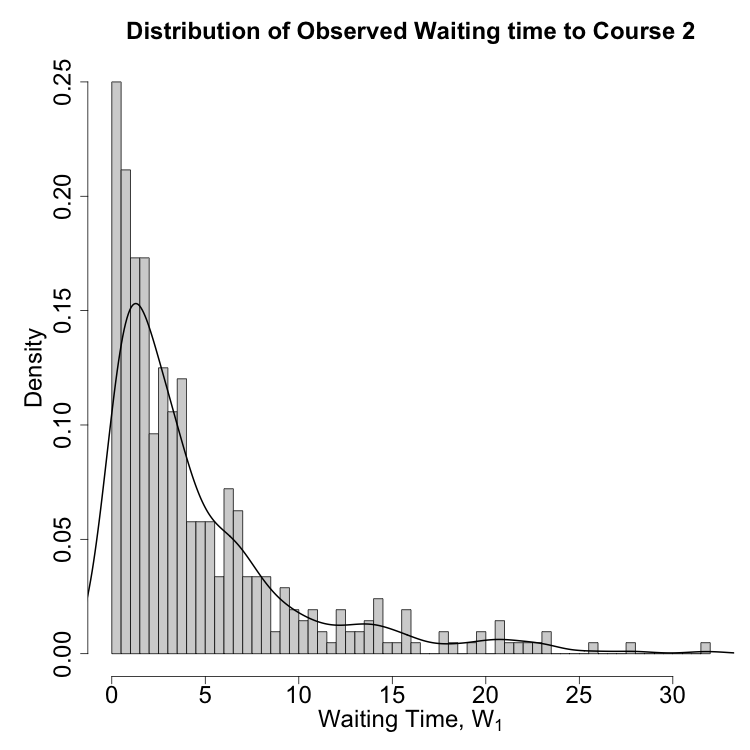
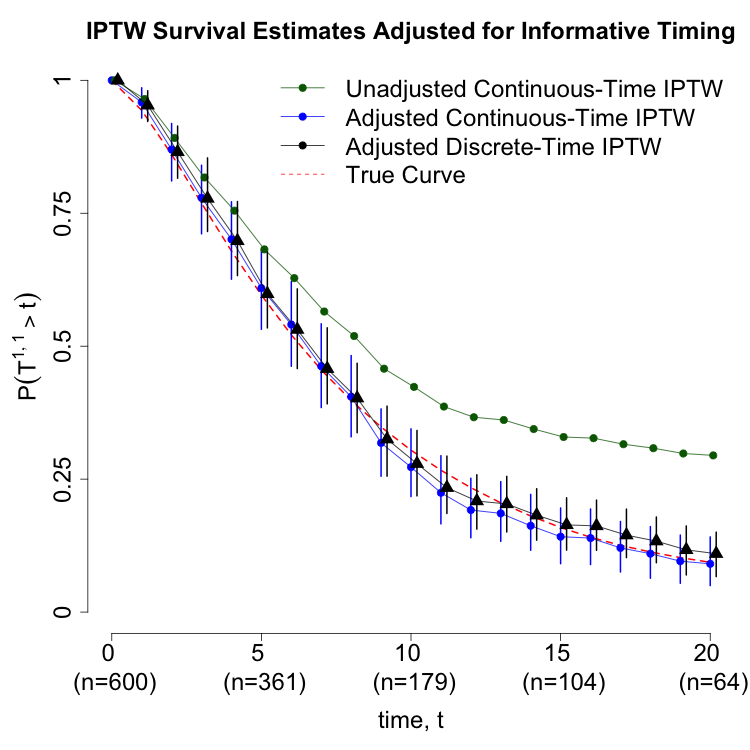
Figure 1: (a) DAG showing waiting times as time-varying confounders; (b) schematic of discrete-time partitioning and treatment assignment intervals.

The identification of causal effects requires sequential exchangeability and positivity assumptions, with explicit conditioning on waiting times. The g-formula for survival probability $P(T^{a_1,a_2} > \tau)$ incorporates sub-density functions for competing risks (death vs. subsequent treatment), and the inverse-probability-of-treatment-weighted (IPTW) estimator is adapted to include waiting times as covariates in propensity score models.

Adjustment Strategies: Continuous-Time and Discrete-Time Approaches

Continuous-Time IPTW Estimation

The continuous-time IPTW estimator for $P(T^{1,1} > \tau)$ is constructed by partitioning contributions from subjects who die before the second treatment and those who survive to receive it. The propensity score for the second treatment is modeled as a function of elapsed time since the first treatment, prior treatment, and covariate history. Simulation results demonstrate that omitting waiting time adjustment leads to substantial bias (8.76% bias, 80.3% coverage), while proper adjustment yields unbiased estimates (0.294% bias, 94.2% coverage).

Handling Censoring

The estimator is further extended to accommodate censoring between treatment courses. The weights are augmented to include inverse probabilities of remaining uncensored, estimated via parametric or semi-parametric survival models. Simulations show that failure to adjust for censoring or informative timing can result in extreme bias (214% bias, 11.9% coverage for unadjusted IPTW under censoring).

Discrete-Time Marginal Structural Models

The discrete-time framework partitions follow-up into intervals, with treatment and covariate assessment only at intervals where treatment occurs. The dynamic treatment rule (DTR) formalism is used to define potential outcomes, and the discrete-time IPTW estimator is constructed analogously, with time-varying weights reflecting both treatment and timing. The identification conditions and adjustment requirements are shown to be agnostic to the choice of time scale (continuous vs. discrete).

Empirical Illustration and Software Implementation

A synthetic dataset mimicking the AML scenario is used to compare continuous-time and discrete-time adjustment strategies. The distribution of waiting times to the second treatment is right-skewed, with a long tail of delayed recovery (Figure 2a). Survival estimates under different adjustment strategies are plotted (Figure 2b): both continuous-time and discrete-time models yield concordant results when waiting time is properly adjusted, while unadjusted models are biased.

Figure 1: (a) Distribution of waiting times to second treatment; (b) Survival estimates under different adjustment strategies.

Implementation details are provided for both approaches, including R code for logistic regression-based propensity score estimation, parametric survival modeling for censoring weights, and pooled logistic regression for discrete-time hazards. The code repository is publicly available.

Theoretical and Practical Implications

The analysis demonstrates that informative timing is a ubiquitous source of bias in longitudinal treatment effect estimation, particularly in clinical settings where treatment initiation is contingent on patient status. The equivalence of continuous-time and discrete-time adjustment strategies, when properly implemented, provides flexibility for applied researchers. The work also clarifies the limitations of approaches that attempt to intervene on the observation process itself, arguing that in many clinical contexts, timing is not intervenable and should be treated as a natural, time-varying confounder.

Future Directions

The paper suggests several avenues for future research, including formal connections between the naturalistic adjustment framework and stochastic interventions on timing, and the development of robust estimators for high-dimensional or irregularly observed covariate processes. The extension to more complex treatment regimes and competing risks is also highlighted.

Conclusion

This work provides a rigorous framework for causal inference with informatively timed treatments, emphasizing the necessity of adjusting for waiting times as time-varying confounders. Both continuous-time and discrete-time g-methods are shown to be effective when properly implemented. The practical guidance and software tools provided facilitate the application of these methods in real-world epidemiological studies, improving the validity of causal effect estimates in the presence of irregular treatment timing.