Quantum Mpemba Effect in Dissipative Spin Chains at Criticality (2508.18906v1)

Abstract: The Quantum Mpemba Effect (QME) is the quantum counterpart of the classical Mpemba effect--a counterintuitive phenomenon in which a system initially at a higher temperature relax to thermal eauilibrium faster than one at a lower temperature. In this work, we investigate the QME in one-dimensional quantum spin chains coupled to a Markovian environment. By analyzing the full relaxation dynamics governed by the Lindblad master equation, we reveal the emergence of a strong quantum Mpemba effect at quantum critical points. Our findings reveal that criticality enhances the non-monotonic dependence of relaxation times on the initial temperature, leading to anomalously accelerated equilibration. This phenomenon is directly linked to the structure of the Liouvillian spectrum at criticality and the associated overlaps with the initial states. These findings demonstrate that quantum phase transitions could provide a natural setting for realizing and enhancing non-equilibrium phenomena in open quantum systems.

• The paper demonstrates that the strong quantum Mpemba effect (sQME) emerges at quantum critical points in dissipative spin chains.
• It leverages the Lindblad master equation and Liouvillian spectral analysis to show accelerated relaxation from zero-temperature states at criticality.
• The study provides experimental and numerical evidence for sQME, highlighting its implications for quantum simulations and efficient state preparation.

Quantum Mpemba Effect in Dissipative Spin Chains at Criticality

Introduction

This paper presents a comprehensive paper of the Quantum Mpemba Effect (QME) in one-dimensional quantum spin chains, specifically focusing on the XXZ and $J_1$-$J_2$ XXZ models under Markovian dephasing dissipation. The QME is a quantum analog of the classical Mpemba effect, where a system initialized further from equilibrium can relax to the steady state faster than one closer to equilibrium. The authors demonstrate that the strong quantum Mpemba effect (sQME) emerges precisely at quantum critical points, with criticality amplifying non-monotonic relaxation dynamics. The analysis is grounded in the spectral properties of the Liouvillian superoperator governing Lindblad evolution, and the results are supported by extensive numerical simulations.

Theoretical Framework

The system is modeled as an open quantum spin chain described by the Lindblad master equation: $$\frac{d\rho(t)}{dt} = \mathscr{L}[\rho(t)] = -i[H_S, \rho(t)] + \mathcal{D}[\rho(t)]$$ where $\mathscr{L}$ is the Liouvillian superoperator and $\mathcal{D}[\rho(t)]$ encodes dephasing-type dissipation via local jump operators $L_j = S^z_j + \mathbb{I}/2$. The steady state is the maximally mixed (infinite-temperature) state, and relaxation dynamics are analyzed via the squared $L^2$-norm distance $$D(t) = \mathrm{Tr}[(\rho(t) - \rho_{\mathrm{ss}})^2]$$.

The XXZ Hamiltonian is given by: $$H = \sum_{n=1}^2 \sum_j J_n \left( S_j^x S_{j+n}^x + S_j^y S_{j+n}^y + \Delta_n S_j^z S_{j+n}^z \right)$$ with critical points at $\Delta = \pm 1$ for the standard XXZ chain and at $J_2/J_1 = -0.25$ for the $J_1$-$J_2$ XXZ model.

Numerical Results: Emergence of sQME at Criticality

XXZ Model

The authors simulate heating dynamics from zero-temperature and finite-temperature initial states. At the ferromagnetic critical point ($\Delta=1$), the zero-temperature state, which is initially farther from equilibrium, relaxes faster than all finite-temperature states, evidenced by trajectory crossings in $D(t)$.

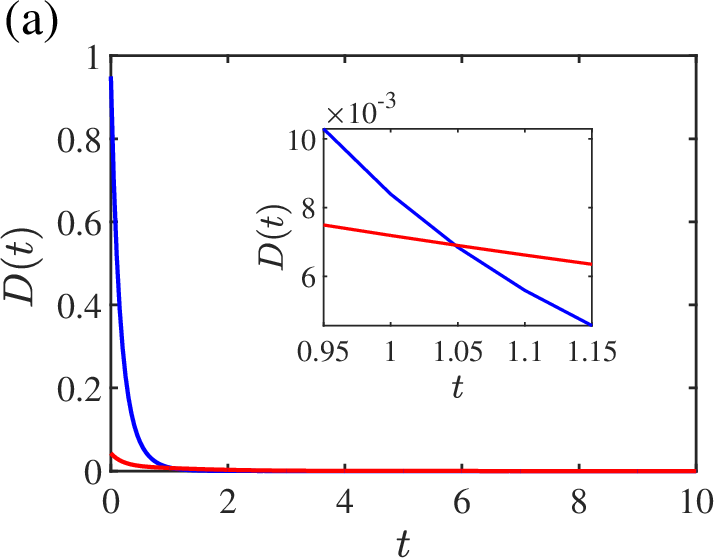
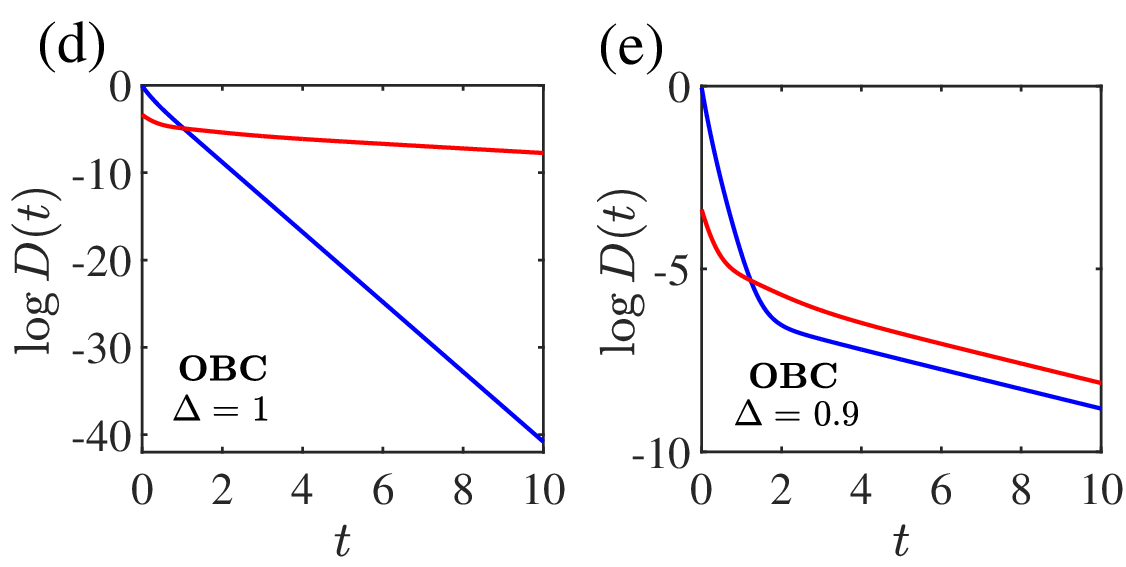
Figure 1: Dynamical evolution in the XXZ model showing sQME at $\Delta=1$ and wQME or absence of QME away from criticality.

The sQME is robust to boundary conditions (periodic or open), but its parameter regime narrows with increasing system size and initial temperature, collapsing to the vicinity of the quantum critical point in the thermodynamic limit.

Figure 2: The parameter range of $\Delta$ supporting QME shrinks with system size and temperature, localizing near the quantum critical point.

At the antiferromagnetic critical point ($\Delta=-1$), a similar sQME is observed, with the mapping between positive and negative temperature states explained by spectral symmetry.

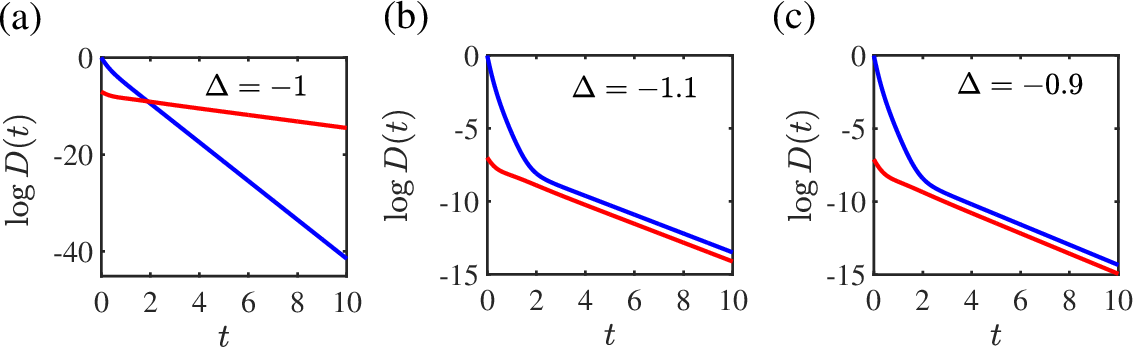
Figure 3: Dynamical evolution near the antiferromagnetic quantum critical point, showing sQME only at $\Delta=-1$.

$J_1$-$J_2$ XXZ Model

The sQME is also found at the quantum phase transition of the $J_1$-$J_2$ XXZ model ($J_2/J_1 > -0.25$, $\Delta=1$). The effect is highly sensitive to the critical point and disappears abruptly when the coupling ratio crosses the threshold.

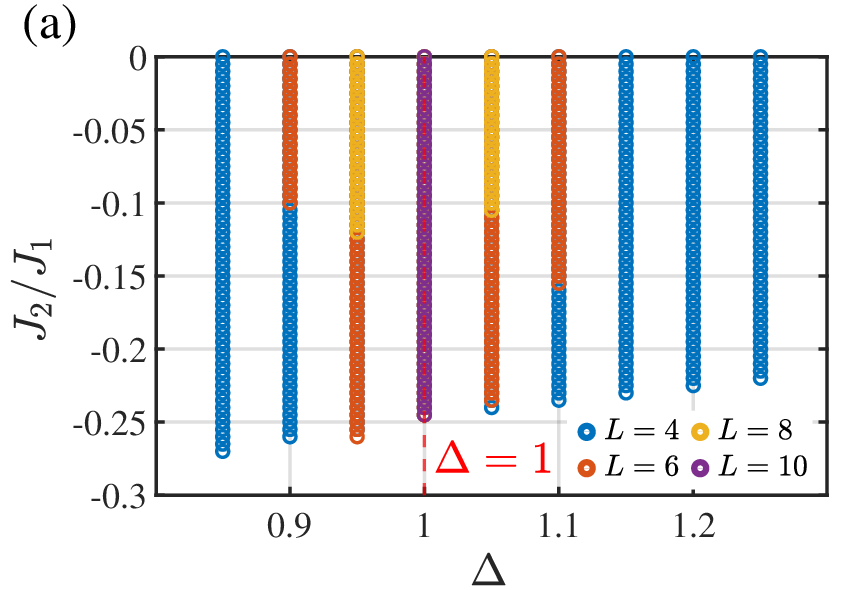
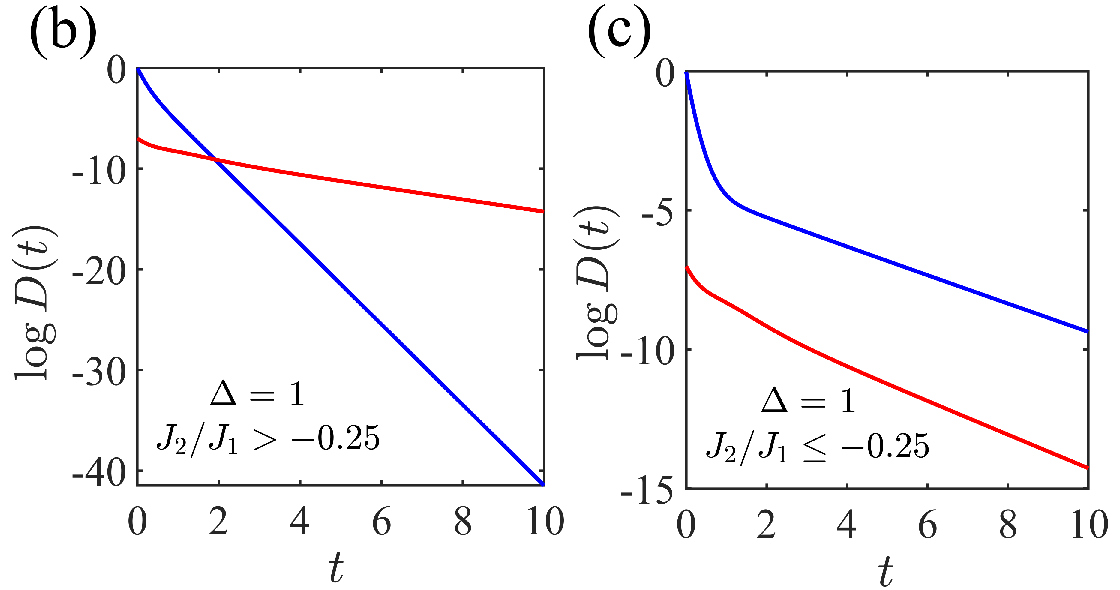
Figure 4: QME in the $J_1$-$J_2$ XXZ model, with sQME only at the critical point and shrinking regime as system size increases.

Mechanism: Liouvillian Spectrum and Overlap Structure

The relaxation dynamics are governed by the Liouvillian spectrum. The sQME arises when the initial state (e.g., zero-temperature ground state) has minimal overlap with slow Liouvillian modes, leading to accelerated relaxation. In contrast, finite-temperature states have significant overlap with slow modes, resulting in slower decay.

Figure 5: Dissipative dynamics and overlap distributions with Liouvillian eigenmodes; zero-temperature state couples to fast modes, finite-temperature states to slow modes.

This spectral mechanism explains both the presence of sQME at criticality and its absence away from critical points or between finite-temperature states.

Experimental Realization

The dissipative XXZ spin chain can be implemented in ultracold atom systems, trapped ions, and superconducting qubit arrays. Dephasing-type dissipation is experimentally accessible via controlled noise or engineered reservoirs. Initial states at different effective temperatures can be prepared, and relaxation dynamics monitored via quantum gas microscopy or similar techniques. The crossing behavior characteristic of sQME is directly observable with current technology.

Implications and Future Directions

The identification of sQME at quantum critical points establishes a direct link between non-equilibrium relaxation dynamics and quantum phase transitions. The QME provides a dynamical probe for criticality and frustrated phases, with potential applications in quantum simulation and state preparation. Theoretical implications include the role of Liouvillian spectral structure in open quantum many-body systems and the sensitivity of anomalous relaxation to system parameters.

Future research directions include:

• Extension to higher-spin chains ($S>1/2$) and higher-dimensional lattices
• Investigation of long-range interactions, non-Markovian environments, and disorder
• Exploration of QME for quantum state engineering and accelerated thermalization

Conclusion

This work demonstrates that the strong quantum Mpemba effect emerges exclusively at quantum critical points in dissipative spin chains, with criticality amplifying non-monotonic relaxation dynamics. The effect is rooted in the overlap structure of initial states with the Liouvillian spectrum, and its experimental realization is feasible with current quantum simulation platforms. The results provide new insights into the interplay between criticality and dissipation, and open avenues for probing and exploiting anomalous relaxation phenomena in open quantum systems.