Lévy processes as weak limits of rough Heston models (2508.14835v1)

Abstract: We show weak convergence of the marginals for a re-scaled rough Heston model to a Normal Inverse Gaussian (NIG) L\'{e}vy process. This shows we can obtain such a limit without having to impose that the true Hurst exponent $H$ for the model is $\frac{1}{2}$ as in [Abi Jaber, & De Carvalho, 2024], or that $H\searrow -\frac{1}{2}$ as in [Abi Jaber, Attal, & Rosenbaum, 2025], so the result potentially has increased financial relevance. We later extend to the case when $V$ has jumps, where we show weak convergence of the finite-dimensional distributions of the integrated variance to a deterministic time-change of the first passage time process to lower barriers for a more general class of spectrally positive L\'{e}vy processes.

• The paper demonstrates weak convergence of re-scaled rough Heston model marginals to a Normal Inverse Gaussian Lévy process without restricting the Hurst exponent.
• It employs advanced stochastic calculus and Volterra integral equations to derive precise convergence results that elucidate the model's scaling behavior.
• The analysis extends to scenarios with jumps in the variance process, supported by numerical evidence, highlighting applications in option pricing and risk management.

Lévy Processes as Weak Limits of Rough Heston Models

Introduction

This paper investigates the connection between rough Heston models and Lévy processes, focusing on their convergence properties. Specifically, the paper demonstrates the weak convergence of the marginals of a re-scaled rough Heston model to a Normal Inverse Gaussian (NIG) Lévy process. A notable aspect of this work is that it achieves this limit without imposing specific restrictions on the Hurst exponent $H$, broadening its applicability in financial contexts. This paper also extends to the scenario where the variance process $V$ has jumps, deriving the convergence of integrated variance distributions to a time-changed Lévy process.

Weak Convergence to NIG Lévy Process

The rough Heston model, recognized for its ability to capture the empirical behavior of volatility time series, is explored under the lens of weak convergence to a NIG Lévy process. By utilizing stochastic calculus and integral equations, the authors show that scaling the rough Heston model appropriately yields weak convergence of its log stock price to a process governed by a Lévy distribution. This theoretical result holds under weakened constraints on the Hurst parameter, compared to prior studies where the parameter was traditionally confined to specific extreme values.

Mathematical Framework

The cornerstone of the analysis is a proposition demonstrating the model's behavior under the scaling limit. The paper provides a detailed derivation using fractional integrals and Volterra integral equations (VIE), highlighting the relationship between the Lévy-Khintchine formula and the NIG process. The authors methodically derive an integral equation central to capturing the model's dynamics and solve it using techniques from functional analysis and stochastic calculus.

Extension to Jump Processes

The paper further explores scenarios where the variance process includes jumps, achieved by incorporating a time-change in the variance's finite-dimensional distributions. This approach reveals that the integrated variance's distributions converge weakly to a more general spectrally positive Lévy process time-changed by a deterministic function. The mathematical treatment of this extension involves sophisticated usage of the Kolmogorov-Riesz-Fréchet compactness theorem and other advanced probabilistic tools.

Numerical Examples and Figures

The authors implement a numerical scheme to approximate solutions of the VIEs involved in the analysis. They provide a figure showing the convergence of solutions as the parameter $\epsilon$ approaches zero, reinforcing the theoretical findings through computational evidence.

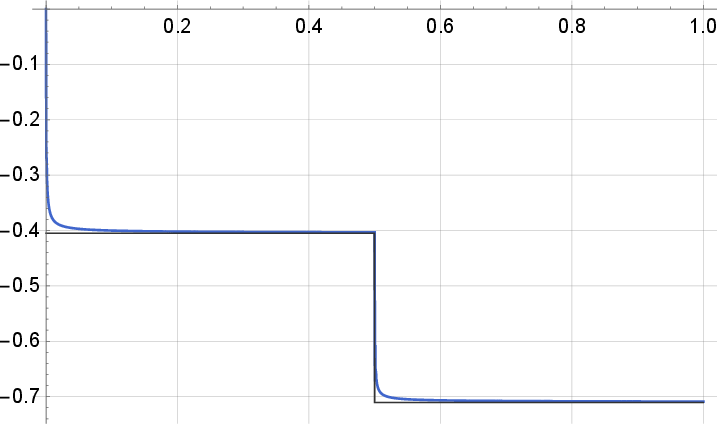
Figure 1: Comparison of the solution $\psi_{\epsilon}$ of the VIE for different $\epsilon$ values, showcasing convergence as $\epsilon \to 0$.

Implications and Future Directions

This paper opens new avenues in mathematical finance, particularly in option pricing and risk management where Lévy processes provide a robust framework. The ability to relate rough Heston models to Lévy processes enhances the models' flexibility and applicability in capturing market behaviors influenced by heavy tails and stochastic volatility. Future research could extend these results to more complex financial derivatives and explore computational strategies for real-time applications.

Conclusion

The paper contributes significantly to the theoretical understanding of rough volatility models by linking them to Lévy processes under weak convergence. By alleviating constraints on the Hurst parameter and incorporating stochastic jumps, it provides a more comprehensive framework applicable in various financial contexts. These advancements pave the way for enriched modeling techniques in quantitative finance, holding potential for immediate practical applications and further theoretical exploration.