Adaptively Robust LLM Inference Optimization under Prediction Uncertainty (2508.14544v1)

Abstract: We study the problem of optimizing LLM inference scheduling to minimize total latency. LLM inference is an online and multi-task service process and also heavily energy consuming by which a pre-trained LLM processes input requests and generates output tokens sequentially. Therefore, it is vital to improve its scheduling efficiency and reduce the power consumption while a great amount of prompt requests are arriving. A key challenge in LLM inference scheduling is that while the prompt length is known upon arrival, the output length, which critically impacts memory usage and processing time, is unknown. To address this uncertainty, we propose algorithms that leverage machine learning to predict output lengths, assuming the prediction provides an interval classification (min-max range) for each request. We first design a conservative algorithm, $\mathcal{A}{\max}$, which schedules requests based on the upper bound of predicted output lengths to prevent memory overflow. However, this approach is overly conservative: as prediction accuracy decreases, performance degrades significantly due to potential overestimation. To overcome this limitation, we propose $\mathcal{A}{\min}$, an adaptive algorithm that initially treats the predicted lower bound as the output length and dynamically refines this estimate during inferencing. We prove that $\mathcal{A}{\min}$ achieves a log-scale competitive ratio. Through numerical simulations, we demonstrate that $\mathcal{A}{\min}$ often performs nearly as well as the hindsight scheduler, highlighting both its efficiency and robustness in practical scenarios. Moreover, $\mathcal{A}_{\min}$ relies solely on the lower bound of the prediction interval--an advantageous design choice since upper bounds on output length are typically more challenging to predict accurately.

• The paper introduces the A_min algorithm that dynamically refines lower bound estimates to optimize LLM inference scheduling under adversarial output uncertainty.
• It rigorously compares the conservative A_max and adaptive A_min methods, demonstrating that A_min achieves a logarithmic competitive ratio even with wide prediction intervals.
• Numerical experiments validate that A_min approaches optimal latency and better utilizes GPU memory, enabling practical integration into large-scale LLM serving systems.

Adaptively Robust LLM Inference Optimization under Prediction Uncertainty

Problem Formulation and Motivation

The paper addresses the operational challenge of scheduling LLM inference requests under output length uncertainty, a critical issue for minimizing latency and energy consumption in large-scale deployments. LLM inference consists of a prefill phase (input prompt processing) and a decode phase (autoregressive token generation), with the output length unknown at request arrival. This uncertainty directly impacts both GPU KV cache memory usage and total processing time, making efficient scheduling nontrivial. The authors formalize the problem as an online, batch-based, resource-constrained scheduling task, where only interval predictions $[\ell, u]$ of output lengths are available, and the true output length $o_i$ is adversarially chosen within this interval.

Benchmark Algorithms and Competitive Analysis

Two primary algorithms are proposed and analyzed:

1. Conservative Max-Length Algorithm ($\mathcal{A}_{\max}$)

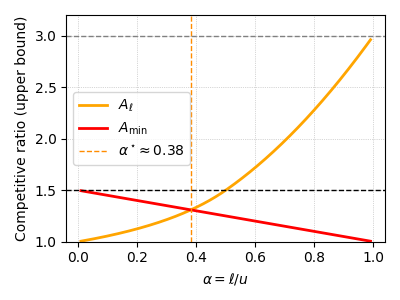
$\mathcal{A}_{\max}$ schedules requests assuming the worst-case output length $u$ for every job, ensuring no memory overflow but often severely underutilizing available memory. The competitive ratio of $\mathcal{A}_{\max}$ is shown to be upper bounded by $\frac{\alpha^{-1}(1+\alpha^{-1})}{2}$ and lower bounded by $\frac{\alpha^{-1}(1+\alpha^{-1/2})}{2}$, where $\alpha = \ell/u$ quantifies prediction accuracy. As $\alpha \to 0$ (i.e., predictions become less precise), the competitive ratio grows unbounded, indicating poor robustness.

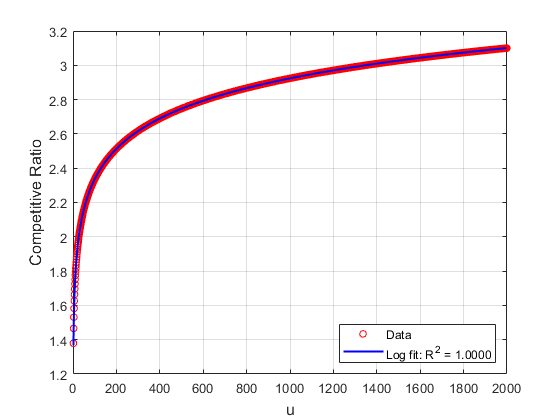
Figure 1: Competitive ratio of $\mathcal{A}_{\max}$ as a function of $\alpha$, illustrating rapid degradation as prediction intervals widen.

2. Adaptive Min-Length Algorithm ($\mathcal{A}_{\min}$)

$\mathcal{A}_{\min}$ initializes each request with the lower bound $\ell$ and dynamically refines this estimate as tokens are generated. When memory overflow is imminent, jobs are evicted in order of increasing accumulated lower bounds, and their lower bounds are updated to reflect progress. This approach leverages only the lower bound, avoiding reliance on the upper bound $u$, which is typically harder to predict accurately.

Theoretical analysis demonstrates that $\mathcal{A}_{\min}$ achieves a competitive ratio of $\mathcal{O}(\log(\alpha^{-1}))$, a significant improvement over $\mathcal{A}_{\max}$, especially for wide prediction intervals. The competitive ratio is derived via a Rayleigh quotient involving the output length distribution, and its spectral radius is shown to scale logarithmically with $u$.

Extensions: Distributional Analysis and Algorithm Selection

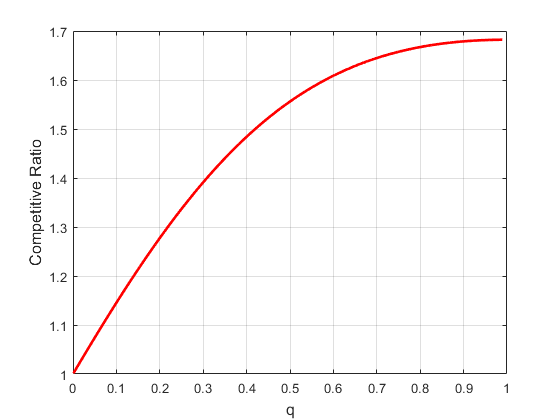
The paper further investigates the performance of $\mathcal{A}_{\min}$ under specific output length distributions:

• Two-point distribution ($\mathcal{D}_2$): All outputs are either $\ell$ or $u$. $\mathcal{A}_{\min}$ achieves a competitive ratio bounded by $1.5$, while a specialized promote-$\ell$ algorithm ($\mathcal{A}_\ell$) can outperform $\mathcal{A}_{\min}$ when $u/\ell > 2.6$.

  Figure 2: Upper-bound curves for the competitive ratios under $\mathcal{D}_2$, showing the regime where $\mathcal{A}_\ell$ is preferable to $\mathcal{A}_{\min}$.

• Geometric and Linearly Weighted Geometric Distributions: For geometric decay, the competitive ratio of $\mathcal{A}_{\min}$ is empirically bounded by $1.7$; for linearly weighted geometric, the theoretical bound is $1.56$.

Figure 3: Competitive ratio as a function of parameter $q$: (Left) geometric distribution $G(p)$; (Right) linearly weighted geometric distribution $LG(p)$.

This distributional analysis enables adaptive algorithm selection based on empirical workload characteristics, further improving robustness.

Numerical Experiments

Experiments on the LMSYS-Chat-1M dataset validate the theoretical findings. Three prediction scenarios are considered:

1. Rough Prediction ($[1,1000]$): $\mathcal{A}_{\max}$ performs poorly due to extreme conservatism, while $\mathcal{A}_{\min}$ matches the hindsight optimal scheduler.
2. Non-Overlapping Classification: As prediction intervals become more accurate, both algorithms improve, but $\mathcal{A}_{\min}$ consistently approaches optimal latency.
3. Overlapping Interval Prediction: With individualized intervals, $\mathcal{A}_{\min}$ maintains low latency even as prediction accuracy degrades, whereas $\mathcal{A}_{\max}$ deteriorates rapidly.

These results confirm the robustness and adaptiveness of $\mathcal{A}_{\min}$ across a range of practical settings.

Implementation Considerations

• Computational Complexity: $\mathcal{A}_{\min}$ operates in $\mathcal{O}(M \log M)$ per time step, where $M$ is the KV cache size.
• Memory Management: The algorithm is compatible with non-preemptive, batch-based LLM serving architectures and can be integrated with existing inference pipelines.
• Prediction Model Integration: Only lower bound predictions are required, which can be efficiently generated via lightweight ML models or heuristics.
• Deployment: The adaptive eviction and batch formation logic can be implemented as a scheduling layer atop standard LLM inference servers, with minimal modification to the underlying model code.

Theoretical and Practical Implications

The paper establishes that robust, adaptive scheduling can dramatically improve LLM inference efficiency under prediction uncertainty, with provable guarantees. The logarithmic competitive ratio of $\mathcal{A}_{\min}$ is a strong result, especially given the adversarial setting. The distributional analysis and adaptive algorithm selection framework provide a pathway for further improvements in real-world systems, where output length distributions are often non-uniform and can be empirically estimated.

The memory-preserving combinatorial proof technique introduced for analyzing latency scaling under memory constraints is broadly applicable to other resource-constrained scheduling problems in AI systems.

Future Directions

Potential avenues for future research include:

• Extending the framework to heterogeneous prompt sizes and multi-worker settings.
• Incorporating multi-metric objectives (e.g., throughput, energy, SLO compliance).
• Leveraging richer prediction models (e.g., quantile regression, uncertainty-aware neural predictors).
• Exploring online learning approaches for dynamic adaptation to changing workload distributions.

Conclusion

This work rigorously advances the theory and practice of LLM inference scheduling under output length uncertainty. The adaptive algorithm $\mathcal{A}_{\min}$ achieves robust, near-optimal latency across a wide range of prediction qualities and output distributions, requiring only lower bound estimates. The results have direct implications for the design of scalable, efficient LLM serving systems, and the analytical techniques developed herein are relevant to a broad class of online scheduling and resource allocation problems in AI operations.