XQuant: Breaking the Memory Wall for LLM Inference with KV Cache Rematerialization (2508.10395v1)

Abstract: Although LLM inference has emerged as a critical workload for many downstream applications, efficiently inferring LLMs is challenging due to the substantial memory footprint and bandwidth requirements. In parallel, compute capabilities have steadily outpaced both memory capacity and bandwidth over the last few decades, a trend that remains evident in modern GPU hardware and exacerbates the challenge of LLM inference. As such, new algorithms are emerging that trade increased computation for reduced memory operations. To that end, we present XQuant, which takes advantage of this trend, enabling an order-of-magnitude reduction in memory consumption through low-bit quantization with substantial accuracy benefits relative to state-of-the-art KV cache quantization methods. We accomplish this by quantizing and caching the layer input activations X, instead of using standard KV caching, and then rematerializing the Keys and Values on-the-fly during inference. This results in an immediate 2$\times$ memory savings compared to KV caching. By applying XQuant, we achieve up to $\sim 7.7\times$ memory savings with $<0.1$ perplexity degradation compared to the FP16 baseline. Furthermore, our approach leverages the fact that X values are similar across layers. Building on this observation, we introduce XQuant-CL, which exploits the cross-layer similarity in the X embeddings for extreme compression. Across different models, XQuant-CL attains up to 10$\times$ memory savings relative to the FP16 baseline with only 0.01 perplexity degradation, and 12.5$\times$ memory savings with only $0.1$ perplexity degradation. XQuant exploits the rapidly increasing compute capabilities of hardware platforms to eliminate the memory bottleneck, while surpassing state-of-the-art KV cache quantization methods and achieving near-FP16 accuracy across a wide range of models.

• The paper presents XQuant, which rematerializes layer input activations (X) instead of storing both K and V, halving the memory footprint.
• It employs uniform quantization and cross-layer delta compression to achieve up to 12.5× memory savings with negligible increases in perplexity.
• XQuant adapts to GQA models using SVD-based down-projection, ensuring compatibility with modern architectures and efficient high-throughput inference.

XQuant: Memory-Efficient LLM Inference via KV Cache Rematerialization

Introduction and Motivation

The increasing deployment of LLMs in production settings has exposed a critical bottleneck: the memory wall. While compute throughput on modern accelerators continues to scale rapidly, memory bandwidth and capacity improvements lag behind, resulting in inference workloads that are predominantly memory bandwidth-bound. This is especially acute for long-context or high-batch inference, where the Key-Value (KV) cache—used to store intermediate activations for attention—dominates memory consumption and bandwidth requirements. Existing approaches to mitigate this, such as direct quantization of the KV cache, are limited by the quantizability of the KV tensors and often require complex, outlier-aware quantization schemes to avoid significant accuracy degradation at low bit-widths.

The XQuant framework addresses this challenge by shifting the focus from KV cache quantization to quantization and rematerialization of the input activations (X) to each transformer layer. This approach leverages the observation that X is more amenable to aggressive quantization and that the cost of recomputing K and V from X is increasingly amortized by the growing compute/memory bandwidth gap.

XQuant Algorithm: Quantizing X and Rematerializing KV

The core idea of XQuant is to cache a quantized version of the post-layernorm input activations X for each layer, rather than the K and V tensors themselves. During inference, the K and V tensors are rematerialized on-the-fly by multiplying the cached X with the respective projection matrices. This approach yields an immediate 2× reduction in memory footprint compared to standard KV caching, as only one tensor per layer is stored instead of two.

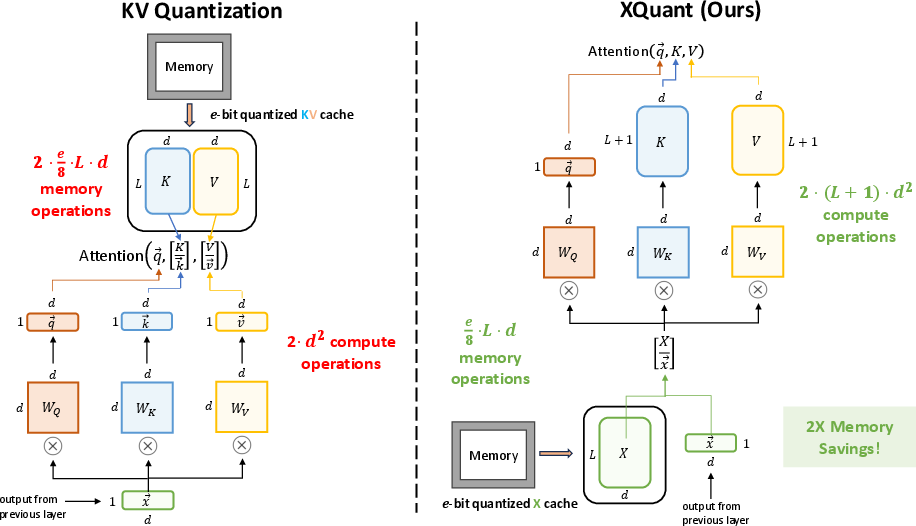
Figure 1: Caching X instead of the KV cache reduces memory footprint and shifts the bottleneck from memory bandwidth to compute, which is increasingly favorable on modern hardware.

This design trades additional compute for reduced memory operations, a tradeoff that is increasingly favorable as LLM inference is memory bandwidth-bound. The rematerialization cost is dominated by matrix multiplications, which are efficiently handled by modern accelerators.

Quantization Strategy

XQuant employs simple uniform quantization for X, without the need for outlier-aware or non-uniform quantization. Empirically, X is found to be more robust to low-bit quantization than K or V, enabling aggressive compression with minimal accuracy loss.

Cross-Layer Delta Compression: Exploiting Residual Stream Structure

A key empirical observation is that the X activations across successive transformer layers are highly similar, a consequence of the residual stream architecture. This motivates a cross-layer compression scheme: instead of quantizing X directly at each layer, XQuant-CL quantizes the delta between the current layer's X and a running accumulator (typically initialized with the first layer's X). The deltas are quantized and cached, and the X for any layer can be reconstructed by summing the base X and the quantized deltas up to that layer.

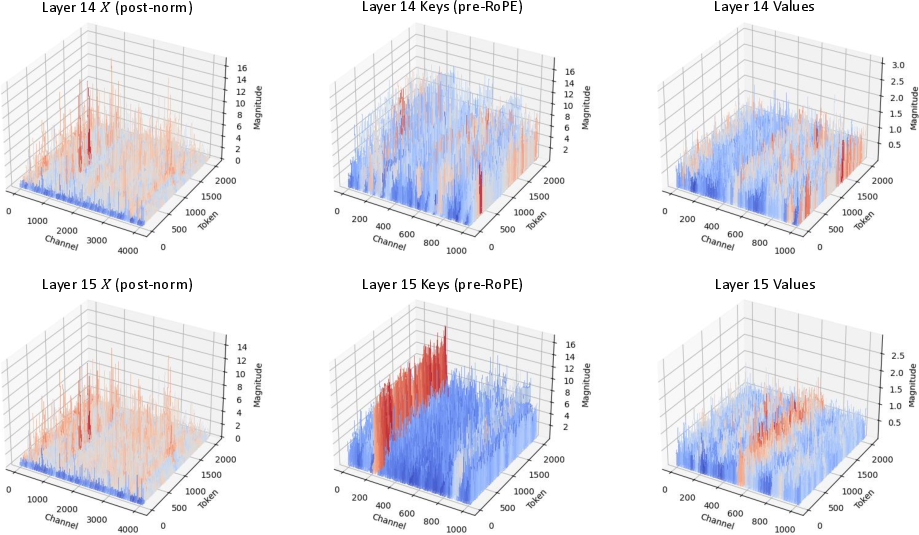
Figure 2: X embeddings across layers are highly similar, in contrast to K and V, enabling effective cross-layer delta compression.

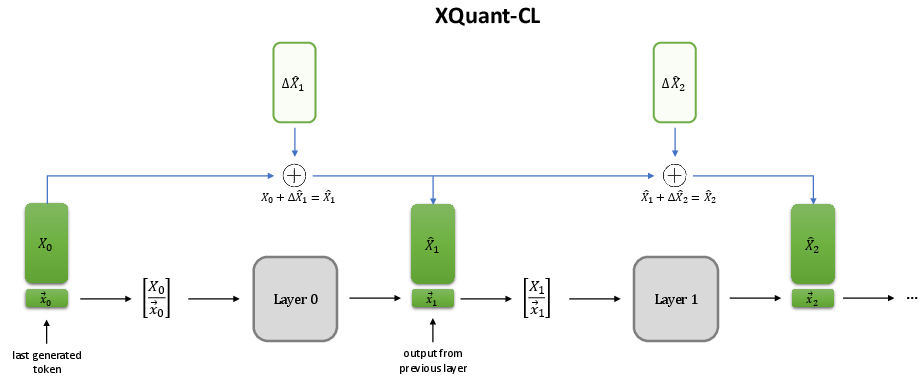
Figure 3: During decoding, each layer's input is reconstructed as the sum of the base X and quantized deltas, with an accumulator to avoid loading all previous deltas.

This approach further reduces the dynamic range of the quantized tensors, enabling even lower bit-width quantization (e.g., 2-3 bits) with negligible accuracy loss. The cross-layer method achieves up to 12.5× memory savings with only 0.1 perplexity degradation relative to FP16, and 10× savings with 0.01 perplexity degradation at 3 bits.

Extension to Grouped Query Attention (GQA) Models

Many modern LLMs employ Grouped Query Attention (GQA), where the K and V projections are computed in a lower-dimensional subspace. Naively applying XQuant to GQA models would increase memory usage, as X is higher-dimensional than the concatenated K and V. To address this, XQuant applies an offline SVD to the K and V projection matrices, and caches the down-projected XU_k and XU_v tensors, which match the dimensionality of the original KV cache.

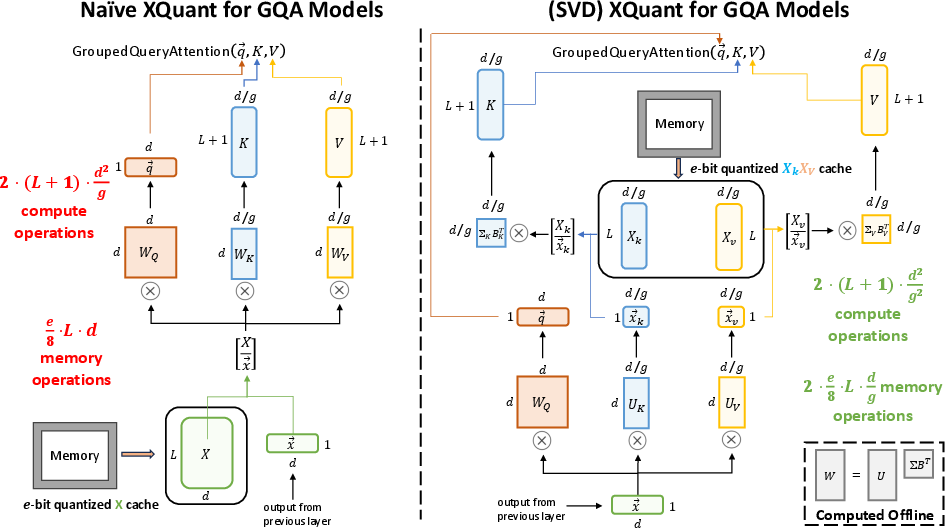
Figure 4: For GQA models, X is down-projected via SVD to match the KV cache size, enabling memory-efficient quantization and rematerialization.

This approach preserves the memory savings of XQuant while maintaining compatibility with GQA architectures. Notably, the down-projected XU_k and XU_v distributions are even more quantization-friendly, with outlier channels concentrated in the first dimension, enabling further optimizations.

System-Level Analysis and Tradeoffs

The paper provides a detailed system-level analysis, quantifying the compute and memory tradeoffs of XQuant and its cross-layer variant. On modern accelerators (e.g., NVIDIA H100), the additional compute required for rematerialization does not become a bottleneck for sequence lengths up to tens of thousands of tokens, as the arithmetic intensity remains below the hardware ridge point. The memory savings directly translate to higher throughput and lower latency in memory-constrained regimes.

Empirical Results

XQuant and its cross-layer variant are evaluated on Llama-2-7B/13B, Llama-3.1-8B, and Mistral-7B models across WikiText-2, C4, LongBench, and GSM8K. Key findings include:

• For the same memory footprint, XQuant achieves up to 0.9 lower perplexity degradation than state-of-the-art KV quantization methods.
• XQuant-CL achieves 10× memory savings with only 0.01 perplexity degradation at 3 bits, and 12.5× savings with 0.1 degradation at 2 bits.
• On downstream tasks (LongBench, GSM8K), XQuant matches or exceeds the accuracy of prior methods at significantly lower memory budgets.
• The method outperforms complex non-uniform and outlier-aware quantization schemes, despite using only uniform quantization.

Analysis of Latent Distributions and Outlier Structure

The SVD-based down-projection for GQA models reveals a structured distribution in the latent XU_k space, with outliers concentrated in the first channel. This property can be exploited by selectively storing the first channel in higher precision or by identifying outlier channels via inspection of the SVD weights, obviating the need for calibration data.

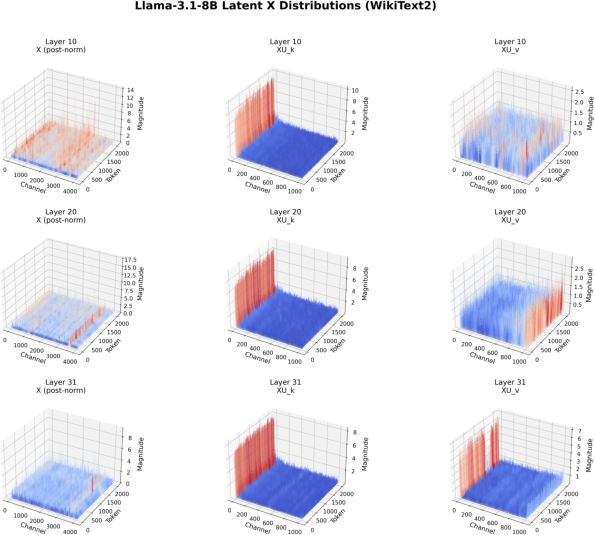
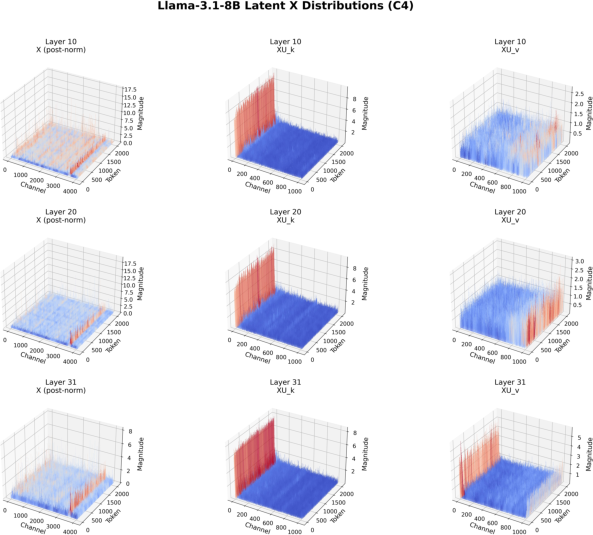
Figure 5: Distributions of X, XU_k, and XU_v for Llama-3.1-8B on WikiText-2 and C4, showing outlier concentration in the first channel of XU_k.

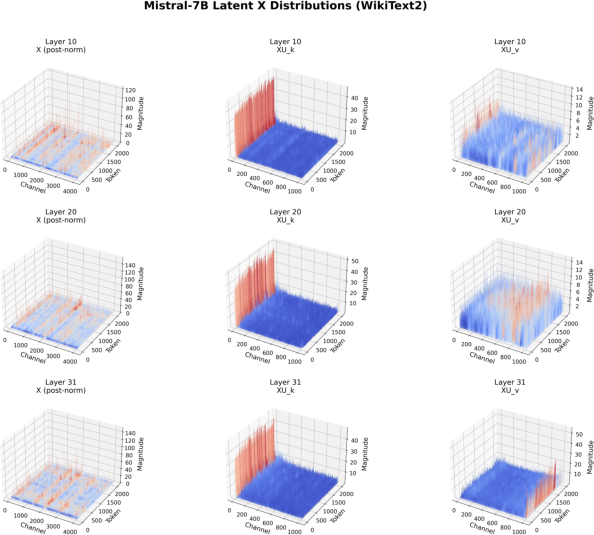
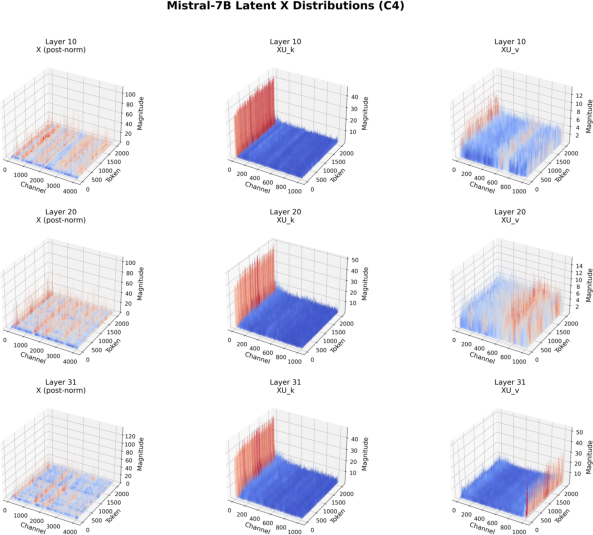
Figure 6: Analogous distributions for Mistral-7B, confirming the generality of the outlier structure.

Practical and Theoretical Implications

XQuant demonstrates that aggressive memory compression for LLM inference is achievable without complex quantization schemes or significant accuracy loss, provided that the right tensor (X) is targeted and the residual structure is exploited. The approach is hardware-forward, anticipating continued divergence between compute and memory scaling. It is compatible with both MHA and GQA architectures, and can be integrated into existing inference frameworks with minimal changes to the attention computation pipeline.

Theoretically, the work highlights the importance of architectural properties (e.g., residual connections) in enabling efficient quantization and compression. The cross-layer delta method leverages the iterative refinement property of residual networks, suggesting further opportunities for structured compression in deep models.

Future Directions

Potential avenues for future research include:

• Hardware/software co-design to further accelerate rematerialization, e.g., via fused kernels or custom accelerators.
• Adaptive precision schemes that dynamically adjust quantization bit-widths based on runtime statistics or task requirements.
• Extension to other model architectures (e.g., vision transformers, multimodal models) and exploration of structured sparsity in the X activations.
• Investigation of the interplay between XQuant and other memory-saving techniques, such as token pruning or attention sparsification.

Conclusion

XQuant provides a principled and empirically validated approach to breaking the memory wall in LLM inference by shifting the focus from KV cache quantization to X quantization and rematerialization. The method achieves substantial memory savings with minimal accuracy loss, outperforms prior state-of-the-art quantization schemes, and is well-aligned with hardware trends. The cross-layer delta compression further exploits the residual structure of transformers for extreme compression. These results have significant implications for the deployment of LLMs in memory-constrained and high-throughput environments, and open new directions for efficient model inference and hardware-aware algorithm design.