Skill Learning via Policy Diversity Yields Identifiable Representations for Reinforcement Learning (2507.14748v1)

Abstract: Self-supervised feature learning and pretraining methods in reinforcement learning (RL) often rely on information-theoretic principles, termed mutual information skill learning (MISL). These methods aim to learn a representation of the environment while also incentivizing exploration thereof. However, the role of the representation and mutual information parametrization in MISL is not yet well understood theoretically. Our work investigates MISL through the lens of identifiable representation learning by focusing on the Contrastive Successor Features (CSF) method. We prove that CSF can provably recover the environment's ground-truth features up to a linear transformation due to the inner product parametrization of the features and skill diversity in a discriminative sense. This first identifiability guarantee for representation learning in RL also helps explain the implications of different mutual information objectives and the downsides of entropy regularizers. We empirically validate our claims in MuJoCo and DeepMind Control and show how CSF provably recovers the ground-truth features both from states and pixels.

• The paper shows that with sufficient policy diversity and an inner product critic, the learned features become identifiable up to a linear transformation of the true state.
• It demonstrates that deficiencies in skill diversity or mismatched latent dimensionality significantly degrade representation quality, as measured by high R² scores in MuJoCo and DMC.
• The work highlights that mutual information objectives on feature differences, rather than maximum-entropy policies, are critical for enforcing geometric constraints and effective skill learning.

Identifiable Representations in Reinforcement Learning via Policy Diversity

Introduction

This work addresses a central theoretical gap in unsupervised skill discovery (USD) and mutual information skill learning (MISL) for reinforcement learning (RL): under what conditions do self-supervised objectives yield representations that are identifiable with respect to the environment's true latent state? The authors focus on the Contrastive Successor Features (CSF) method, providing the first identifiability guarantees for representation learning in RL. The analysis leverages recent advances in nonlinear independent component analysis (ICA) and causal representation learning (CRL), connecting the success of MISL to the interplay between policy diversity and inner product parametrization in the critic.

Theoretical Framework and Identifiability

The paper formalizes the RL setting as a partially observable Markov decision process (POMDP) without extrinsic rewards, where the agent observes $o = g(s)$, with $g$ a deterministic generator, and learns a representation $\phi(o)$. Skills $z$ are sampled from a prior $p(z)$, and the policy $\pi(a|o, z)$ is conditioned on both the observation and the skill. The critic $q(z|\phi(o), \phi(o'))$ is parametrized as an inner product and trained with a contrastive loss.

The key insight is that, under sufficient policy diversity and an inner product critic, the learned features $\phi(o)$ are identifiable up to a linear transformation of the true state $s$. The identifiability result is established by matching the assumptions of nonlinear ICA—specifically, the existence of a diverse set of skills spanning the latent space, and the conditional distribution of state transitions $p(s'-s|z)$ following a von Mises-Fisher (vMF) distribution centered at $z$. The contrastive loss used in CSF is shown to be equivalent to a cross-entropy loss, which is critical for identifiability in the nonlinear ICA framework.

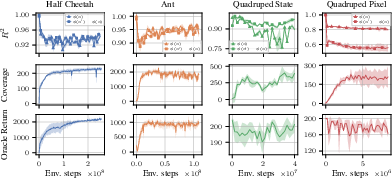
Figure 2: CSF identifies the underlying states in MuJoCo and DMC up to a linear transformation, as measured by $R^2$ between learned features and ground-truth states.

Empirical Validation

The authors empirically validate their theoretical claims in both state-based and pixel-based MuJoCo and DeepMind Control Suite environments. They demonstrate that CSF recovers the ground-truth features with high $R^2$ scores, both for the features themselves and their differences, confirming linear identifiability. Notably, in pixel-based settings, the learned features remain highly linearly related to the underlying states, though the feature differences are less so, reflecting the increased complexity of the observation mapping.

Role of Skill Diversity and Latent Dimensionality

A central practical implication is the necessity of skill diversity for identifiability. The authors show that if the set of skills does not span the latent space, identifiability and state coverage degrade. This is demonstrated by varying the number of skills and comparing fixed versus resampled skill sets.

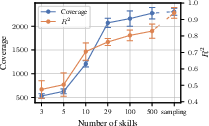
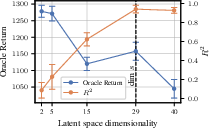
Figure 4: The effect of skill diversity on state identifiability and coverage in the Ant environment. Insufficient skill diversity leads to lower $R^2$ and state coverage.

Additionally, the dimensionality of the latent space is shown to be critical. If the feature space is lower-dimensional than the true state space, identifiability is lost, and not all state information is linearly decodable. However, for zero-shot task transfer, a lower-dimensional bottleneck can sometimes be beneficial, though the optimal dimensionality for identifiability matches the state space.

Figure 1: The effect of latent space dimensionality on state identifiability and coverage. Identifiability requires the feature space to match or exceed the state dimensionality.

Mutual Information Objectives and Policy Regularization

The analysis reveals that the specific mutual information objective matters for the geometry of the learned feature space. Optimizing $I(s, s'; z)$ via feature differences enforces a locality constraint, ensuring that consecutive state embeddings are close but distinct, whereas $I(s; z)$ can lead to degenerate solutions (e.g., collapsed or antipodal features). This geometric constraint is essential for learning meaningful representations.

A notable negative result is that maximum-entropy policies, often used to encourage exploration, are suboptimal for skill diversity in this context. A maximum-entropy policy breaks the dependence between skills and state transitions, violating the diversity condition required for identifiability.

Practical Implications and Recommendations

• Skill Diversity: Ensure that the skill set spans the latent space; resampling skills or using a sufficiently large fixed set is necessary for identifiability and exploration.
• Inner Product Critic: Use an inner product parametrization in the critic to guarantee identifiability, as justified by nonlinear ICA theory.
• Latent Dimensionality: Match the feature space dimensionality to the true state space for maximal identifiability; lower-dimensional bottlenecks may aid transfer but at the cost of linear decodability.
• Policy Regularization: Avoid strong entropy regularization in skill-conditioned policies, as it undermines the diversity required for identifiability.
• Objective Design: Prefer mutual information objectives that operate on feature differences (e.g., $I(s, s'; z)$) to enforce geometric constraints in the latent space.

Implications and Future Directions

The theoretical and empirical results provide a principled explanation for the success of recent MISL methods and clarify the role of architectural and algorithmic choices. The identifiability guarantees bridge RL, self-supervised learning, and causal representation learning, suggesting that diverse interventions (skills) are essential for learning world models that are useful for downstream tasks and generalization.

Future work should investigate the generality of these results beyond the considered environments, the impact of partial observability and non-injective observation mappings, and the extension to more complex or hierarchical skill spaces. Additionally, the connection to causal representation learning opens avenues for integrating interventional data and domain shifts into RL pretraining.

Conclusion

This work establishes the first identifiability guarantees for representation learning in RL via policy diversity and inner product parametrization, grounded in nonlinear ICA theory. The results provide both theoretical justification and practical guidance for the design of self-supervised RL algorithms, highlighting the necessity of skill diversity, appropriate critic parametrization, and careful objective selection. These insights are expected to inform future developments in unsupervised skill discovery, world model learning, and generalizable RL agents.