DeepONet as a Multi-Operator Extrapolation Model: Distributed Pretraining with Physics-Informed Fine-Tuning (2411.07239v1)

Abstract: We propose a novel fine-tuning method to achieve multi-operator learning through training a distributed neural operator with diverse function data and then zero-shot fine-tuning the neural network using physics-informed losses for downstream tasks. Operator learning effectively approximates solution operators for PDEs and various PDE-related problems, yet it often struggles to generalize to new tasks. To address this, we investigate fine-tuning a pretrained model, while carefully selecting an initialization that enables rapid adaptation to new tasks with minimal data. Our approach combines distributed learning to integrate data from various operators in pre-training, while physics-informed methods enable zero-shot fine-tuning, minimizing the reliance on downstream data. We investigate standard fine-tuning and Low-Rank Adaptation fine-tuning, applying both to train complex nonlinear target operators that are difficult to learn only using random initialization. Through comprehensive numerical examples, we demonstrate the advantages of our approach, showcasing significant improvements in accuracy. Our findings provide a robust framework for advancing multi-operator learning and highlight the potential of transfer learning techniques in this domain.

• The paper demonstrates that combining distributed pretraining with physics-informed fine-tuning improves DeepONet’s ability to learn and extrapolate multiple PDE operators.
• The approach reduces data dependency by leveraging diverse operator datasets and incorporating governing physical laws for zero-shot adaptation.
• Significant improvements were observed in solving Burgers’, porous media, and diffusion-reaction equations compared to traditional single-operator training.

DeepONet as a Multi-Operator Extrapolation Model: Distributed Pretraining with Physics-Informed Fine-Tuning

The paper "DeepONet as a Multi-Operator Extrapolation Model: Distributed Pretraining with Physics-Informed Fine-Tuning" examines the integration of DeepONet with distributed pretraining and physics-informed (PI) fine-tuning to enhance multi-operator learning and extrapolation. This approach addresses the limitations of traditional operator learning methods by reducing data requirements and improving accuracy across different scenarios.

Background and Methodology

The foundation of this research is the integration of DeepONet, a neural operator framework designed to map functions to functions effectively. DeepONet traditionally struggles with generalization across different operators, especially when initial conditions lack sufficient similarity to the test functions. To overcome this, the research introduces a combination of distributed learning for pretraining and PI fine-tuning.

Distributed Pretraining: This involves training a model on a diverse dataset composed of multiple operators rather than focusing on data from a single operator. The distributed neural operators (D2NO/MODNO) framework leverages this multivariate dataset, creating a robust initialization by averaging models trained on distinct operator data (Figure 1).

Figure 1: Methodology demonstration for downstream PDE $u_t - u_{xx}$ with initial condition (IC) and Dirichlet boundary conditions (BC).

Physics-Informed Fine-Tuning: PI fine-tuning leverages governing physical laws to guide the model's adaptation to new tasks with minimal data, enabling zero-shot adaptation. Techniques like PINN enrich the neural operator by embedding physical principles, thereby enhancing the model's prediction capacity without extensive data.

Experimental Results

The experiments demonstrate that D2NO pretrained models show significant improvements over models initialized with either single-operator pretraining or random initialization. Distinct sets of partial differential equations (PDEs) such as Burgers', porous media, and diffusion-reaction equations were evaluated, showcasing the framework's adaptability:

• Burgers' Equation: Pretraining with multiple similar operators resulted in a robust initialization that reduced extrapolation errors considerably compared to random initialization.

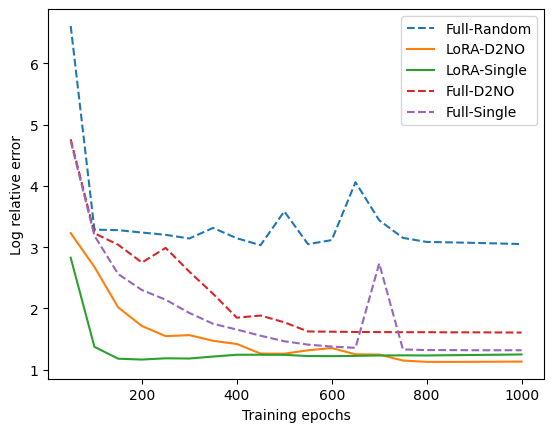
Figure 2: Left: Relative error (in log scale) decay with respect to training epochs. Three full tuning curves are dashed lines, and two LoRA training curves are solid lines. The final relative errors are presented in Table 1.

• Porous Media and Diffusion-Reaction Equations: The experiments on non-linear PDEs corroborated the effectiveness of the proposed strategy, with the MODNO/D2NO pretraining displaying superior performance across different tasks.

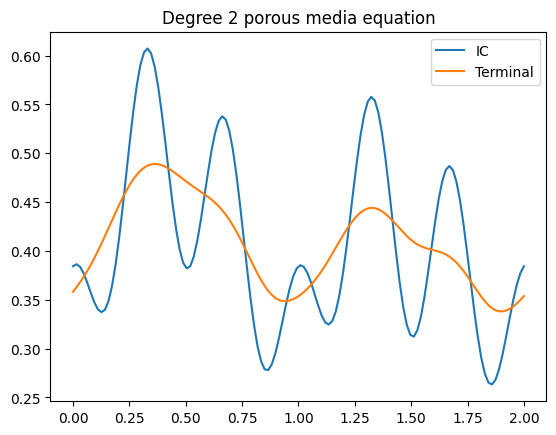
Figure 3: Demonstration for two solution operators: Diffusion-reaction system with varying reaction terms and porous media systems showcasing model adaptability.

Analysis and Discussion

The proposed approach allows the neural operator to generalize well across tasks even when the underlying operators differ significantly. By utilizing distributed datasets, the model gains a broad understanding of functional behavior, thereby facilitating robust initializations for fine-tuning. PI approaches complement this by providing a mechanism to embed domain-specific knowledge directly into the model, reducing dependency on data-intensive training or fine-tuning processes.

Overall, the framework shows promise in various domains, suggesting potential extensions in scientific machine learning, engineering simulations, and other computational sciences. Future work may explore extending this framework with uncertainty quantification techniques to enhance reliability in predictions, especially in physics and engineering applications.

Conclusion

The integration of DeepONet with distributed pretraining and physics-informed fine-tuning offers a significant advancement in operator learning. By effectively addressing issues related to data scarcity and task generalization, the approach ensures high adaptability and performance across diverse applications. This paper contributes to the understanding of how multi-operator learning and fine-tuning can be systematically combined to tackle complex learning objectives in artificial intelligence.