Neuro-symbolic Learning Yielding Logical Constraints (2410.20957v1)

Abstract: Neuro-symbolic systems combine the abilities of neural perception and logical reasoning. However, end-to-end learning of neuro-symbolic systems is still an unsolved challenge. This paper proposes a natural framework that fuses neural network training, symbol grounding, and logical constraint synthesis into a coherent and efficient end-to-end learning process. The capability of this framework comes from the improved interactions between the neural and the symbolic parts of the system in both the training and inference stages. Technically, to bridge the gap between the continuous neural network and the discrete logical constraint, we introduce a difference-of-convex programming technique to relax the logical constraints while maintaining their precision. We also employ cardinality constraints as the language for logical constraint learning and incorporate a trust region method to avoid the degeneracy of logical constraint in learning. Both theoretical analyses and empirical evaluations substantiate the effectiveness of the proposed framework.

• The paper presents a neuro-symbolic framework that integrates neural perception with logical reasoning using bilevel optimization and difference-of-convex programming.
• The methodology focuses on efficient symbol grounding and leveraging cardinality constraints, enhancing performance on tasks like visual Sudoku solving and self-driving simulations.
• Empirical evaluations show improved accuracy and reliable convergence, paving the way for AI systems that effectively balance intuitive and logical reasoning.

Neuro-symbolic Learning Yielding Logical Constraints

Introduction to Neuro-symbolic Systems

The paper "Neuro-symbolic Learning Yielding Logical Constraints" focuses on developing a framework that integrates neural perception with symbolic reasoning. Neuro-symbolic systems aim to combine the pattern recognition capabilities of neural networks with the interpretability and generalization potential of symbolic logic. This approach attempts to merge System 1 (intuitive and fast thinking) and System 2 (deliberate and logical reasoning) theories as described by Kahneman.

Framework Description

The proposed framework is built on a bilevel optimization problem that incorporates both neural network learning and logical constraint synthesis. The authors address the semantic gap between end-to-end learning by implementing a mechanism for efficient symbol grounding. This bridges the intermediate symbol latency issue and enables weakly supervised learning where only inputs and final outputs are given, without intermediate labels.

The logical constraints are structured as cardinality constraints and are optimized through difference-of-convex (DC) programming to manage the Boolean constraints effectively. The framework also employs trust region methods to prevent degeneracy in learning logical constraints, ensuring robustness during training and inference.

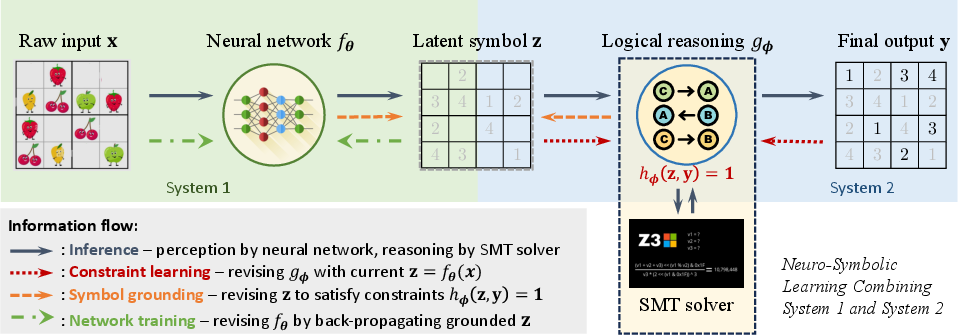
Figure 1: An example of neuro-symbolic learning for visual Sudoku solving. In this task, the neural network transforms the puzzle image into symbols, while symbolic reasoning solves the puzzle.

Efficient Constraint Learning

For logical constraints representation, the paper uses cardinality constraints which express logic by limiting the number of true variables. This method improves the flexibility and precision of logic extracted from neural outputs. To enhance learning effectiveness, they apply a trust region method to mitigate constraint degeneracy, which occurs when constraints become trivial or oversimplified.

Additionally, Boolean constraints are relaxed using DC programming, enabling the conversion of non-convex problems into approachable convex optimization issues.

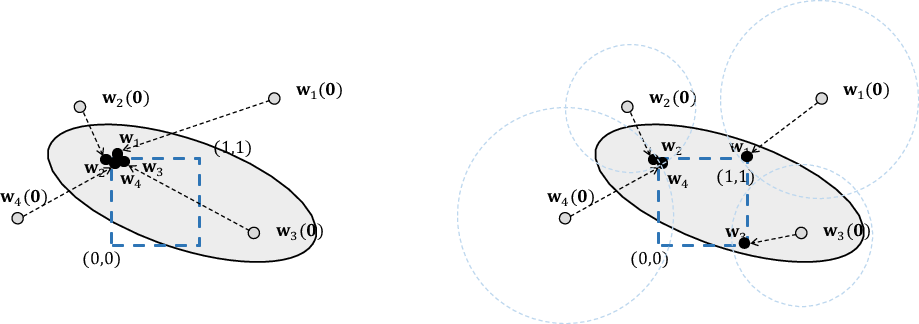
Figure 2: Avoid degeneracy by trust region method. Boolean constraints and stochastic gradient descent may lead to degeneracy in logical constraints.

Algorithm Design and Analysis

The algorithm involves iterative updates of logical constraints and the neural network:

1. Logical constraints are updated based on neural predictions and observed outputs using the Proximal Point Algorithm (PPA).
2. Symbol grounding is adjusted to satisfy learned constraints, correcting the neural predictions.
3. Neural networks are updated using stochastic gradient descent based on the adjusted symbol grounding.

Convergence of this method is guaranteed by theoretical analysis, suggesting efficient joint training of perception and reasoning components.

Empirical Evaluations

The proposed framework was tested on solving visual Sudoku puzzles, chained XOR tasks, and path planning in self-driving simulations.

In the Sudoku task, the framework demonstrated notable accuracy improvements over existing methods, efficiently learning and applying logical constraints.

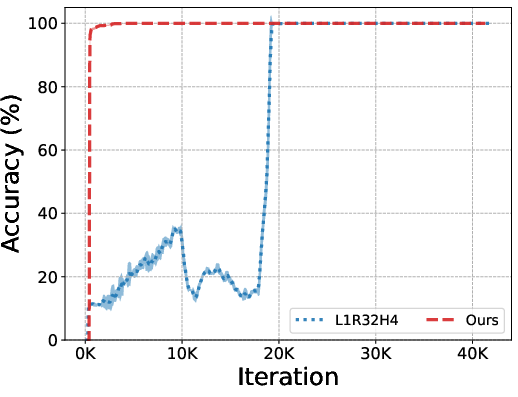
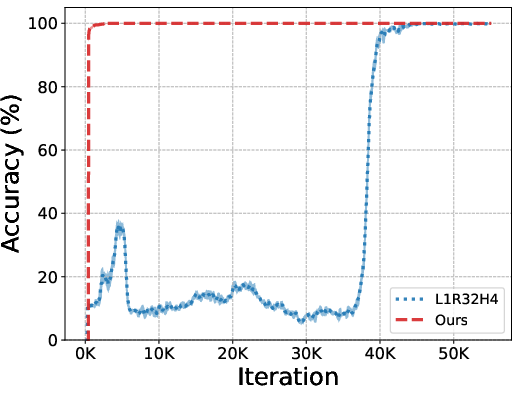
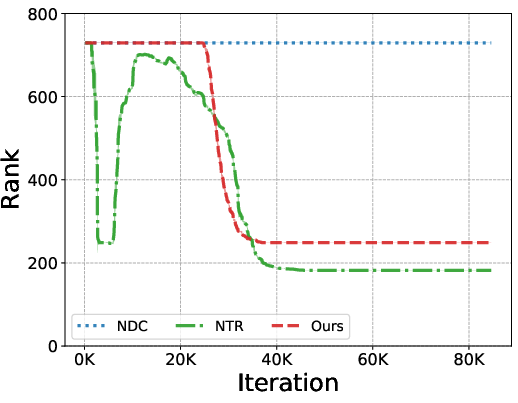
Figure 3: Training curves of accuracy (left) and rank (right). The approach shows enhanced symbol grounding and precise convergence to constraints.

In self-driving tasks, the system effectively planned paths by integrating obstacle detection and logical reasoning, outperforming prior models in terms of path accuracy and reliability.

Figure 4: A neuro-symbolic system in self-driving tasks, integrating neural perception for obstacle detection and symbolic reasoning for path planning.

Limitations and Future Directions

Despite its efficacy, the framework's reliance on cardinality constraints presents challenges in capturing complex logical structures. Furthermore, the computational demand during inference, particularly with large logical problem domains, limits scalability. Future work could enhance reasoning efficiency and explore more expressive logical representations, possibly incorporating LLMs.

Conclusion

This paper's neuro-symbolic framework advances the integration of neural networks and logical reasoning, demonstrating superior performance across diverse tasks. It shows significant promise for applications requiring both precise perception and interpretable reasoning, paving the way for future AI systems that balance intuition and logic effectively.