Towards Reliability-Aware Active Distribution System Operations: A Sequential Convex Programming Approach (2410.14011v1)

Abstract: The increasing demand for electricity and the aging infrastructure of power distribution systems have raised significant concerns about future system reliability. Failures in distribution systems, closely linked to system usage and environmental factors, are the primary contributors to electricity service interruptions. The integration of distributed energy resources (DER) presents an opportunity to enhance system reliability through optimized operations. This paper proposes a novel approach that explicitly incorporates both decision- and context-dependent reliability into the optimization of control setpoints for DERs in active distribution systems. The proposed model captures how operational decisions and ambient temperature impact the likelihood of component failures, enabling a balanced approach to cost efficiency and reliability. By leveraging a logistic function model for component failure rates and employing a sequential convex programming method, the model addresses the challenges of non-convex optimization under decision-dependent uncertainty. Numerical case study on a modified IEEE $33$-bus test system demonstrates the effectiveness of the model in dynamically adjusting power flows and enhancing system robustness under varying environmental conditions and operational loads. The results highlight the potential of DERs to contribute to distribution system reliability by efficiently managing power flows and responding to fluctuating energy demands.

• The paper proposes a sequential convex programming algorithm that integrates decision-dependent failure probabilities to enhance system reliability.
• It combines cost minimization with reliability metrics using logistic regression and iterative linearization to optimize DER operations.
• The approach effectively reduces expected energy-not-served costs through dynamic DER setpoint adjustments, validated on an IEEE 33-bus test system.

Sequential Convex Programming for Reliability-Aware Active Distribution Systems

Introduction

The paper "Towards Reliability-Aware Active Distribution System Operations: A Sequential Convex Programming Approach" focuses on enhancing the reliability of power distribution systems amidst growing electricity demand and aging infrastructure. Failures in distribution systems predominantly cause power outages, influenced by operational decisions and environmental factors. The integration of Distributed Energy Resources (DER) offers opportunities to improve system reliability. This research introduces a novel framework incorporating reliability metrics dependent on decisions and context, optimizing DER control setpoints using a sequential convex programming method.

Model Description

Distribution System Configuration

The paper models an active distribution system operator (DSO) managing a radial network with DERs such as DGs, BESSs, and DR programs. The system's dynamics are captured using the DistFlow AC OPF formulation, incorporating ambient temperature-dependent capacity adjustments for DGs and lines.

Cost-Only Model (CM)

In the baseline CM, the objective is minimizing operational cost by controlling the DERs. The cost function includes energy purchased from the grid and energy used from local DERs, modeled with specific cost parameters.

Cost-and-Reliability Model (CRM)

CRM extends CM by including expected energy-not-served (EENS) cost, accounting for component failure probabilities. The failure probability model uses a logistic regression approach, considering both operational context (e.g., temperatures) and decision-dependent factors (power flows).

Optimization Approach

Non-Convex Challenges

CRM poses a non-convex optimization problem due to its decision-dependent uncertainty. The paper introduces a sequential convex programming approach to approximate and solve this problem iteratively.

Iterative Solution Method

The algorithm initiates with CM and refines the solution by linearizing the non-convex CRM objective around the current solution estimate. Regularization techniques ensure controlled updates during iterations.

Case Study Details

Setup

A modified IEEE 33-bus test system serves as the case paper. Load profiles are adjusted to reflect temporal changes, and temperature impacts are modeled.

Regression Model Estimation

Using simulated data, the paper employs weighted bootstrapping alongside Hamiltonian Markov Chain methods to estimate logistic regression parameters crucial for failure rate modeling.

Numerical Results

CRM dynamically adjusts DER setpoints to optimize the trade-off between operational cost and reliability, effectively reducing the expected cost of unserved energy. This is achieved through strategic utilizations such as BESS charging during low demand and discharging during peak hours.

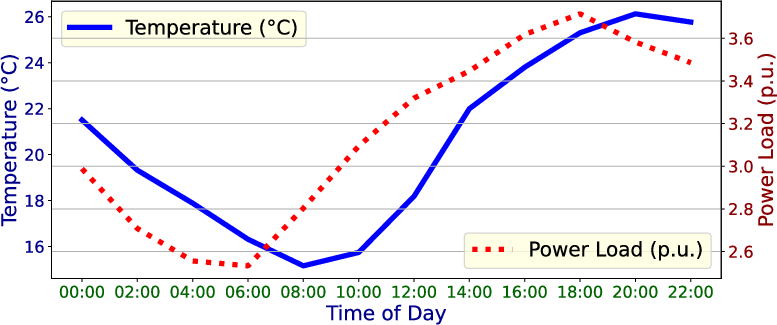
Figure 1: Temperature and load profile of the considered day. Load is total load across all buses: $\sum_{i\in\mathcal{N}p_{i,t}^{\rm c}\ \forall t$.

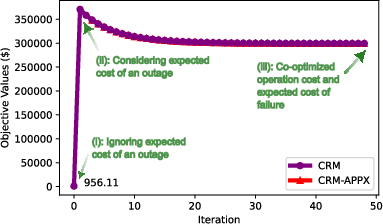
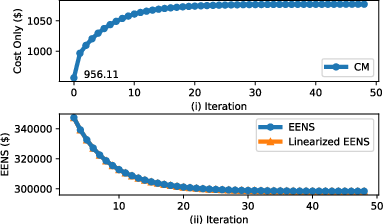
Figure 2: CRM {additional_guidance} CRM-APPX objective vs Iteration.

Conclusion

The proposed approach efficiently addresses the reliability challenges in distribution systems by integrating DER operation decisions with failure probability modeling. It highlights the potential of DERs to substantially enhance system reliability while balancing operational costs. Future research will focus on incorporating tie-line switches for fault isolation, performance scalability, and machine learning for function approximation.