Image Vectorization with Depth: convexified shape layers with depth ordering

Abstract: Image vectorization is a process to convert a raster image into a scalable vector graphic format. Objective is to effectively remove the pixelization effect while representing boundaries of image by scaleable parameterized curves. We propose new image vectorization with depth which considers depth ordering among shapes and use curvature-based inpainting for convexifying shapes in vectorization process.From a given color quantized raster image, we first define each connected component of the same color as a shape layer, and construct depth ordering among them using a newly proposed depth ordering energy. Global depth ordering among all shapes is described by a directed graph, and we propose an energy to remove cycle within the graph. After constructing depth ordering of shapes, we convexify occluded regions by Euler's elastica curvature-based variational inpainting, and leverage on the stability of Modica-Mortola double-well potential energy to inpaint large regions. This is following human vision perception that boundaries of shapes extend smoothly, and we assume shapes are likely to be convex. Finally, we fit Bézier curves to the boundaries and save vectorization as a SVG file which allows superposition of curvature-based inpainted shapes following the depth ordering. This is a new way to vectorize images, by decomposing an image into scalable shape layers with computed depth ordering. This approach makes editing shapes and images more natural and intuitive. We also consider grouping shape layers for semantic vectorization. We present various numerical results and comparisons against recent layer-based vectorization methods to validate the proposed model.

• The paper presents a novel method integrating depth ordering with a new energy function to resolve shape layer hierarchies, overcoming traditional vectorization limitations.
• It employs curvature-based inpainting using Euler's elastica to convexify shape boundaries, ensuring smooth and coherent vector representations.
• The method achieves lower MSE, higher PSNR, and improved computational efficiency compared to existing techniques, enhancing post-processing editability.

Image Vectorization with Depth: Convexified Shape Layers with Depth Ordering

Introduction

The paper "Image Vectorization with Depth: Convexified Shape Layers with Depth Ordering" (2409.06648) introduces a novel method for image vectorization that incorporates depth ordering and curvature-based inpainting. Image vectorization transforms raster images into vector graphics, allowing for scalability without loss of quality. Traditional vectorization approaches often neglect geometric coherence and depth perception, resulting in visually inconsistent outputs. This paper overcomes these limitations by proposing a method that computes depth ordering among shape layers using a newly defined energy function, followed by curvature-based inpainting to ensure smooth and convex vector representations.

Methodology

The proposed approach begins with color quantization of the raster image, where each distinct color forms a shape layer. The depth ordering among these shape layers is determined using a novel depth ordering energy, defined as the difference between covered area measures. This measure reflects human visual perception assumptions, positing that convex shapes and those with less occluded regions are likely to be in front.

A directed graph is constructed to represent global depth ordering, where nodes correspond to shape layers and directed edges indicate relative depth positions. Cycles in this graph are resolved using an energy-based method to break edges with minimal perceptual implausibility, thus ensuring a linear global order.

Each shape layer is then convexified using Euler's elastica-based inpainting within occluded regions dictated by the depth ordering. This process smoothens and extends shape boundaries according to curvature-driven assumptions, adhering to natural visual percepts. The inpainted shapes are fitted with B{e}zier curves for final vectorization, stored as scalable vector graphics (SVG), maintaining depth coherence.

Numerical Results and Comparisons

The vectorization method demonstrates effective depth layering and convexification across various images, ranging from simple geometric shapes to complex natural scenes. The method is computationally efficient and offers superior visual fidelity compared to existing layer-based vectorization methods like LIVE and DiffVG, particularly in preserving fine details and shape semantics.

Numerical comparisons indicate that the proposed method achieves lower mean squared error (MSE) and higher peak signal-to-noise ratio (PSNR) than its counterparts, while maintaining significantly reduced computational complexity. The depth-ordered layers facilitate easy post-processing modifications, such as element removal or position adjustments, directly through SVG manipulations.

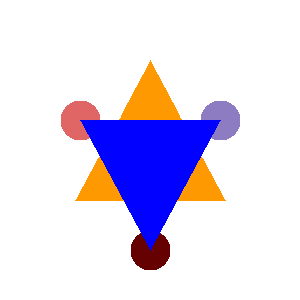
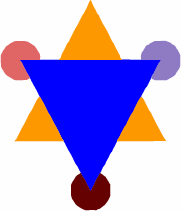
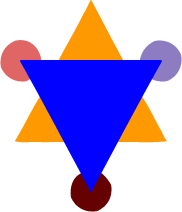
Figure 1: A comparison of the depth layering effect in different scenarios. Various occluded toppings and features are reconstructed as convex shapes with depth ordering.

Practical Implications and Future Developments

The proposed method's ability to vectorize images with semantic depth ordering holds implications for fields like graphic design, animation, and augmented reality, where scalable and editable vector graphics are essential. The approach allows for intuitive editing and manipulation of vectorized images, enhancing user interactivity and creative flexibility.

Future work could explore incorporating neural network models to refine depth estimation and shape grouping, potentially enhancing vectorization quality for complex scenes. Moreover, extending the framework to dynamically handle lighting variations and translucency effects could broaden its applicability.

Conclusion

The paper presents a robust method for integrating depth perception into image vectorization, blending geometric fidelity with visual semantics. By combining depth ordering and elastica-based inpainting, the approach offers a significant advancement in the field of scalable vector graphics, paving the way for more sophisticated and interactive image processing techniques.