Tensor-based quantum phase difference estimation for large-scale demonstration (2408.04946v3)

Abstract: We develop an energy calculation algorithm leveraging quantum phase difference estimation (QPDE) scheme and a tensor-network-based unitary compression method in the preparation of superposition states and time-evolution gates. Alongside its efficient implementation, this algorithm reduces depolarization noise affections exponentially. We demonstrated energy gap calculations for one-dimensional Hubbard models on IBM superconducting devices using circuits up to 32-system (plus one-ancilla) qubits, a five-fold increase over previous QPE demonstrations, at the 7242 controlled-Z gate level of standard transpilation, utilizing a Q-CTRL error suppression module. Additionally, we propose a technique towards molecular executions using spatial orbital localization and index sorting, verified by a 13- (17-)qubit hexatriene (octatetraene) simulation. Since QPDE can handle the same objectives as QPE, our algorithm represents a leap forward in quantum computing on real devices.

• The paper introduces a tensor-based QPDE algorithm that replaces controlled gates with MPO compression for efficient quantum phase difference estimation.
• It demonstrates significant gate reduction and enhanced error resilience on IBM superconducting devices through energy gap calculations in quantum systems.
• The method scales up to 33-qubit circuits for molecular simulations and Hubbard models, paving the way for robust large-scale quantum computations.

Tensor-Based Quantum Phase Difference Estimation for Large-Scale Demonstration

This paper introduces an advanced algorithm utilizing Quantum Phase Difference Estimation (QPDE) with a tensor-based approach, primarily aimed at energy gap calculations in quantum systems. This research demonstrates significant improvements in computational efficiency and noise resilience in quantum computations, particularly focusing on scalability to larger qubit systems.

Algorithm Overview

The proposed algorithm builds on traditional Quantum Phase Estimation (QPE) techniques but substitutes the expensive controlled time-evolution gates with a more efficient tensor-network-based unitary compression method. The approach involves preparing superposition states and time-evolution operators as Matrix Product Operators (MPOs), thereby minimizing the circuit complexity while mitigating depolarization noise.

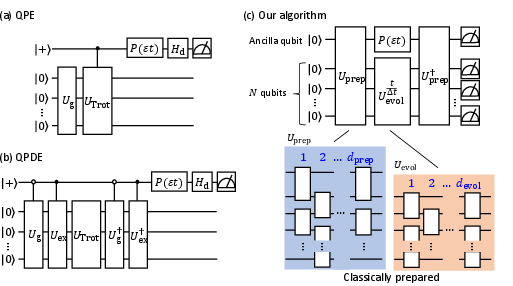
Figure 1: Circuits for the Bayesian QPE-type algorithms and our algorithm. In all the figures, the topmost qubit is an ancilla qubit and the others are system qubits. $P(x)$ is a phase gate.

The QPDE method is depicted in Figure 1. The method avoids the prohibitive cost of controlled operations by employing a classically prepared compressed operator for the initial and evolution gates. This bypasses numerous complications associated with conventional QPE.

Implementation and Performance

Unitary Compression

The paper details a rigorous procedure for approximating time evolution in an MPO form, thereby facilitating its implementation on quantum circuits with less overhead. This approach significantly reduces the number of two-qubit gates required compared to conventional methods. The resulting MPO-based circuits were implemented on IBM superconducting quantum devices, showing a notable reduction in gate complexity.

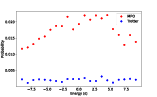
Figure 2: Comparison of the time evolution circuits (nine qubits) using the Eagle device ibm_osaka.

As Figure 2 demonstrates, the time evolution circuit compression reduces gate requirements without significant loss of fidelity, compared to first-order Trotter approximations.

Real-World Application Demonstration

The algorithm was applied to calculate energy gaps in one-dimensional Hubbard models and other quantum chemical systems like hexatriene. The effective deployment of up to 33 qubit circuits on real quantum devices represents a five-fold increase in scale over previous implementations.

Figure 3: Demonstration of our algorithm in the one-dimensional Hubbard models using (a) the noiseless simulator and (b,c,d) the Heron device ibm_torino with the error suppression.

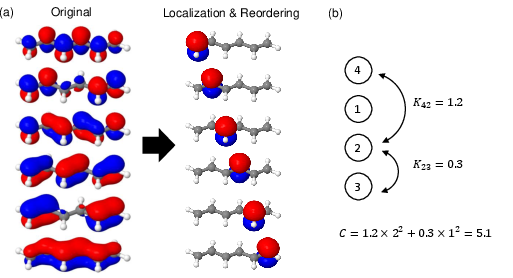
Figure 4: Procedure for converting the molecular Hamiltonian to a one-dimensional one.

Error Resilience and Noise Mitigation

A key result is the enhanced error resilience provided by the algorithm. By encoding operations as MPOs, the algorithm effectively suppresses depolarizing noise exponentially with respect to the number of qubits, as shown in Figure 3. This robustness in noise environments highlights its potential for large-scale implementations.

Molecular Simulations

The paper extends its application to molecular systems, demonstrating the algorithm in hexatriene and octatetraene simulations. By transforming molecular Hamiltonians into one-dimensional forms, the execution on 13- and 17-qubit circuits with error suppression displays operational feasibility beyond small-scale proofs of concept.

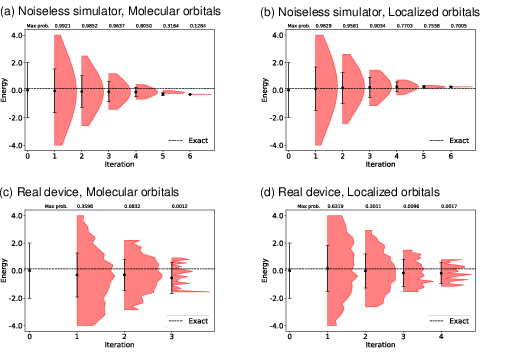
Figure 5: Demonstration of our algorithm in hexatriene (13-qubit circuit) using (a,b) the noiseless simulator and (c,d) the Heron device ibm_torino with the error suppression.

Conclusion

The research presented illustrates significant advancements in the quantum simulation domain through tensor-based QPDE. By facilitating larger qubit systems with enhanced error mitigation techniques, the algorithm establishes itself as a robust tool for complex quantum computations, potentially extending into areas previously deemed intractable using classical or earlier quantum algorithms. Future developments may focus on further optimizing tensor networks for varied hardware architectures and integrating hybrid classical-quantum approaches for enhanced accuracy and scalability.