Generalised Circuit Partitioning for Distributed Quantum Computing (2408.01424v2)

Abstract: Distributed quantum computing (DQC) is a new paradigm aimed at scaling up quantum computing via the interconnection of smaller quantum processing units (QPUs). Shared entanglement allows teleportation of both states and gates between QPUs. This leads to an attractive horizontal scaling of quantum processing power, which comes at the expense of the additional time and noise introduced by entanglement sharing protocols. Consequently, methods for partitioning quantum circuits across multiple QPUs should aim to minimise the amount of entanglement-based communication required between distributed QPUs. Existing protocols tend to focus primarily on optimising entanglement costs for gate teleportation or state teleportation to cover operations between QPUs, rather than both at the same time. The most general form of the problem should treat gate and state teleportation on the same footing, allowing minimal cost circuit partitions through a combination of the two. This work introduces a graph-based formulation which allows joint optimisation of gate and state teleportation cost, including extensions of gate teleportation which group gates together for distribution using common resources. The formulation permits low e-bit cost for a variety of circuit types. Using a basic genetic algorithm, improved performance over state-of-the-art methods is obtained in terms of both average e-bit cost and time scaling.

• The paper presents a unified graph-based formulation that optimizes both state and gate teleportation to reduce entanglement-based communication costs.
• It compares the GCP-S and GCP-E methods with leading techniques, demonstrating superior e-bit cost reduction across various quantum circuit benchmarks.
• The proposed genetic algorithm scales linearly with circuit dimensions, offering faster compilation times and improved scalability for distributed quantum processing.

Generalised Circuit Partitioning for Distributed Quantum Computing

The paper "Generalised Circuit Partitioning for Distributed Quantum Computing" (2408.01424) introduces a comprehensive approach to address the distributed quantum computing (DQC) problem, where the aim is to partition quantum circuits across multiple quantum processing units (QPUs) efficiently. The focus is on minimizing the entanglement-based communication cost, which is a significant bottleneck due to the time and noise introduced by entanglement sharing protocols. This essay will explore the methodology, results, and implications of the proposed approach.

Methodological Approach

Unified Graph-Based Formulation

The paper proposes a unified graph-based formulation for optimizing both gate and state teleportation costs simultaneously. Unlike existing methods that focus on either gate teleportation or state teleportation, the presented approach allows for a combined treatment. This comprehensive formulation utilizes a graph-based representation to model circuit interactions over time, facilitating a dynamic partitioning strategy.

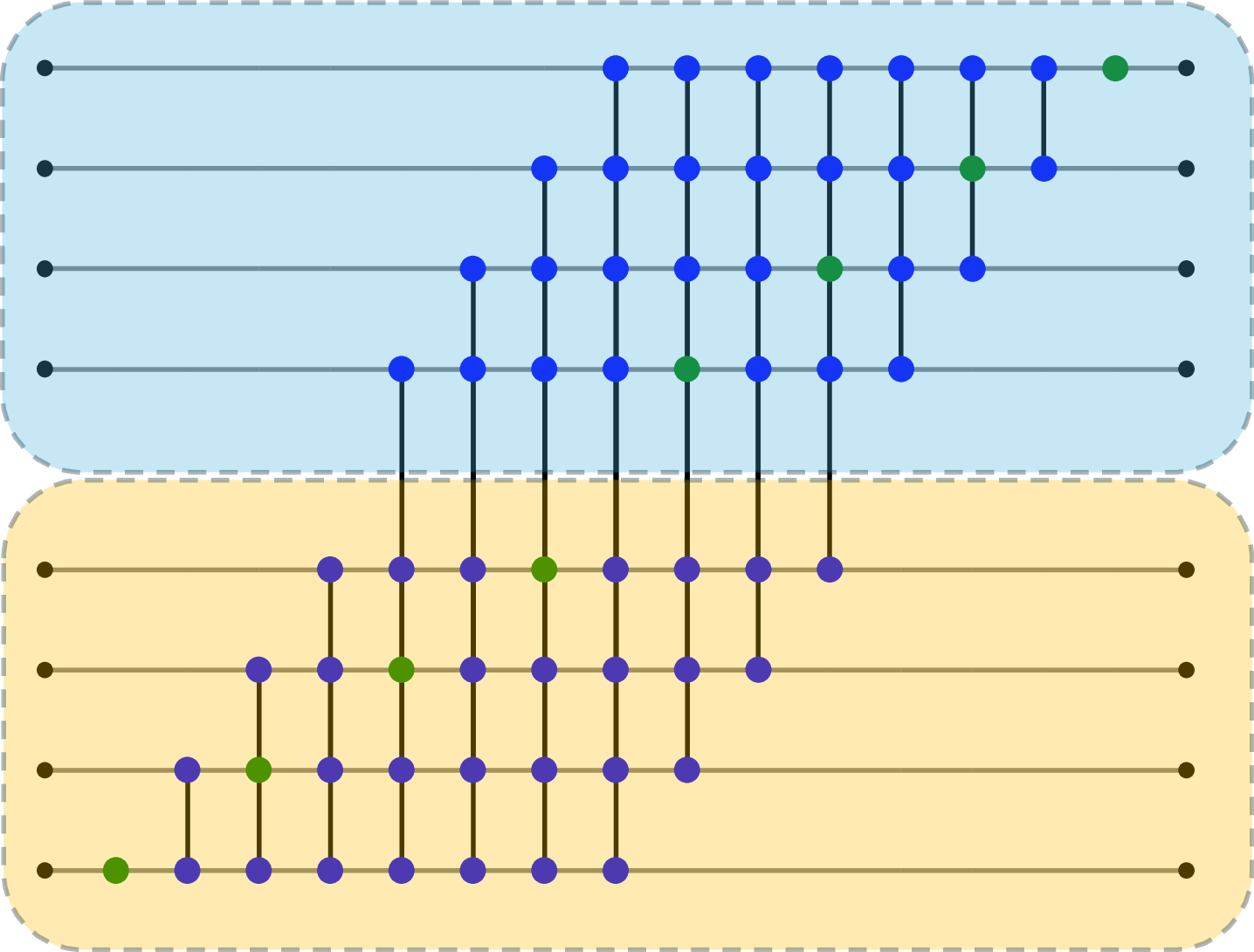
Figure 2: Extended circuit interaction graph. The graph shown here depicts a QFT circuit on eight qubits, with an unoptimized static mapping indicating gate teleportation for edges cutting the partition.

Under the Generalised Circuit Partitioning (GCP) method, the circuit is transformed into an extended interaction graph that captures qubit interactions across time steps. By applying a genetic algorithm (GA) with time complexity scaling linearly with the product of circuit width and depth, the solution space is efficiently explored.

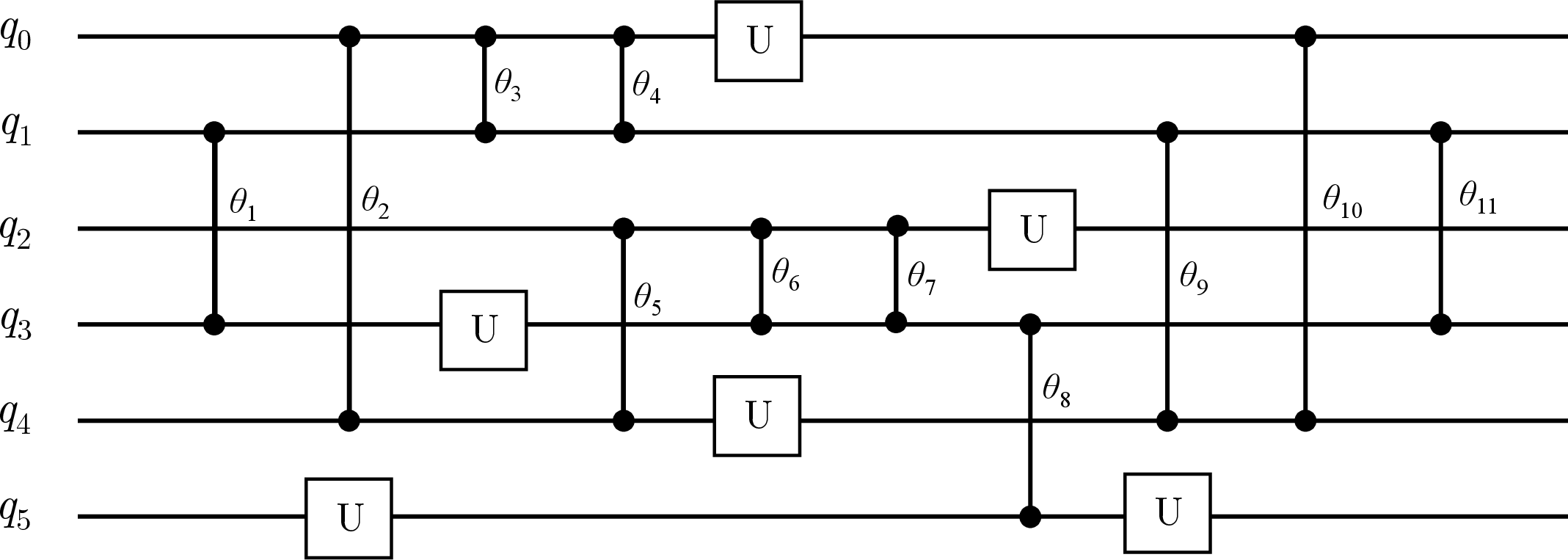
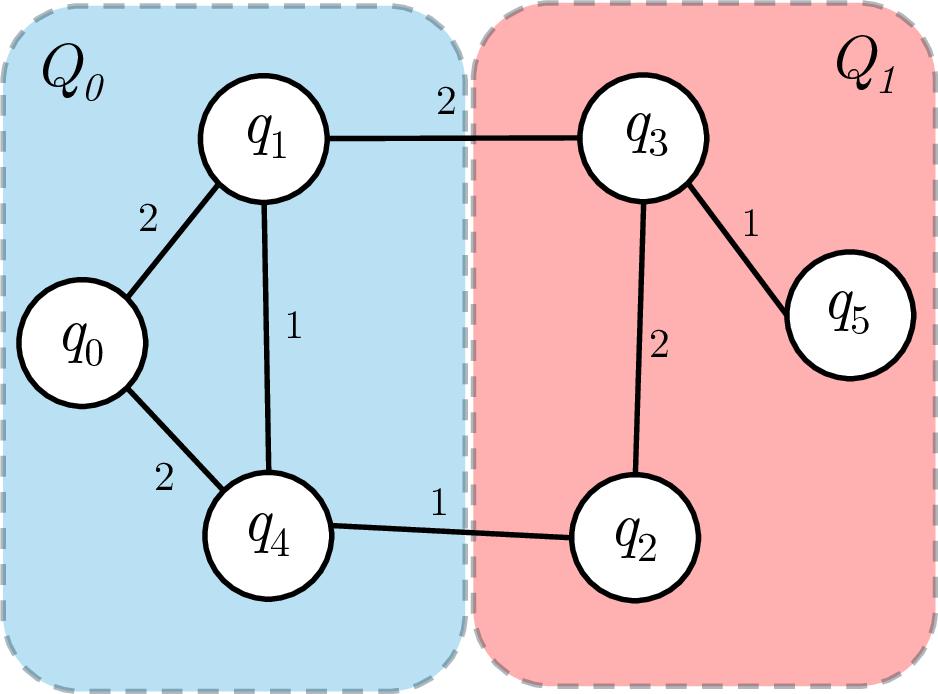
Figure 2: Extended circuit interaction graph. The graph shown here represented a QFT circuit on eight qubits. All nodes are statically assigned, indicating gate teleportation for edges cutting the partition.

Comparative Analysis

The paper extends to a performance comparison with leading partitioning methods, including Fine-Grained Partitioning (FGP-rOEE) and gate packing methods like AESD. These methods exhibit high e-bit performance for certain circuit structures compared to the established benchmarks; however, they lack adequate flexibility to leverage both state and gate teleportation optimally in all scenarios.

Figure 2: Random quantum circuit. See section \ref{sec:cp_frac}.

In particular, the FGP method by Baker et al. (Baker et al., 2020) relies solely on state teleportation, using sequences of interaction graphs for each circuit layer and looking ahead to optimize the assignment of qubits and non-local operations covered by state teleportation. This results in low-cost assignment sequences for circuits with consistent qubit connectivity, but performance degrades when qubit connectivity is not constant.

Conversely, gate packing methods emphasize extended gate teleportation for reducing e-bit costs, employing strategies to group and teleport sequences of gates using fewer e-bits, which can result in significant savings in specific circuit scenarios.

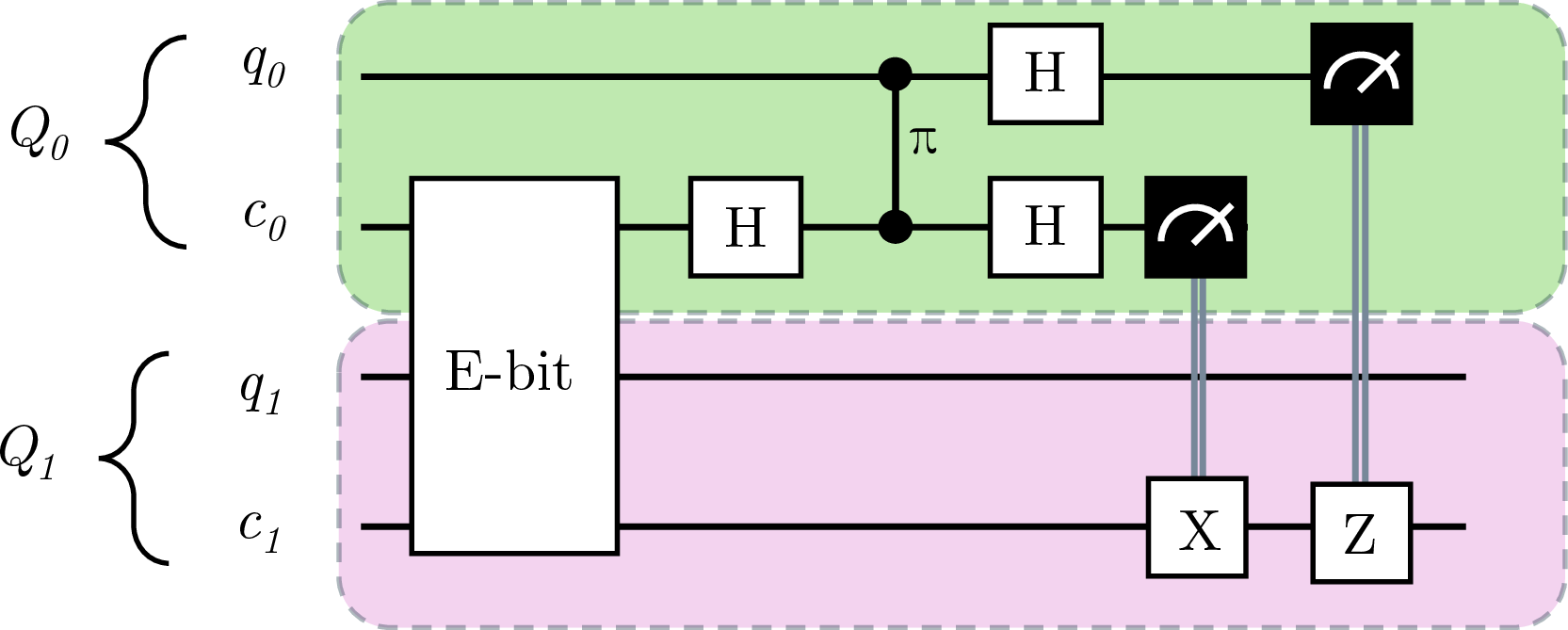
Figure 3: State teleportation. This is the well known quantum teleportation procedure implemented using a controlled-phase gate rather than a CNOT.

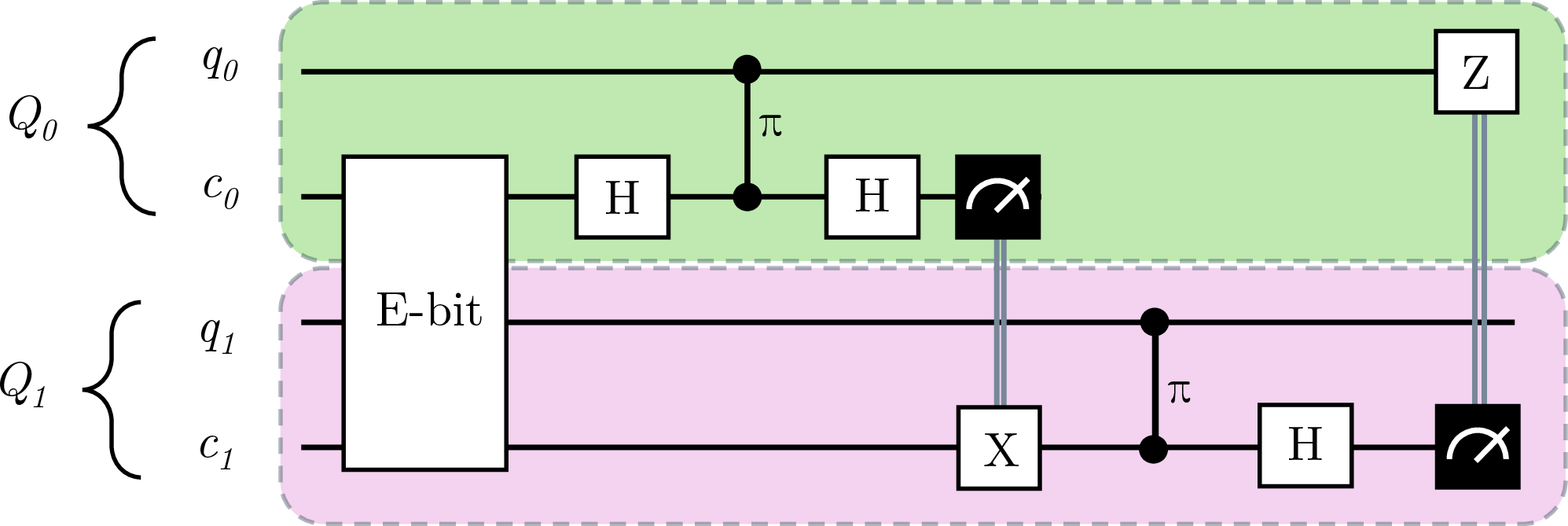
Figure 4: Gate teleportation. The circuit displays how a single controlled-phase gate can be teleported using an e-bit. The procedure is general to all controlled-unitary gates with $q_0$ as the control.

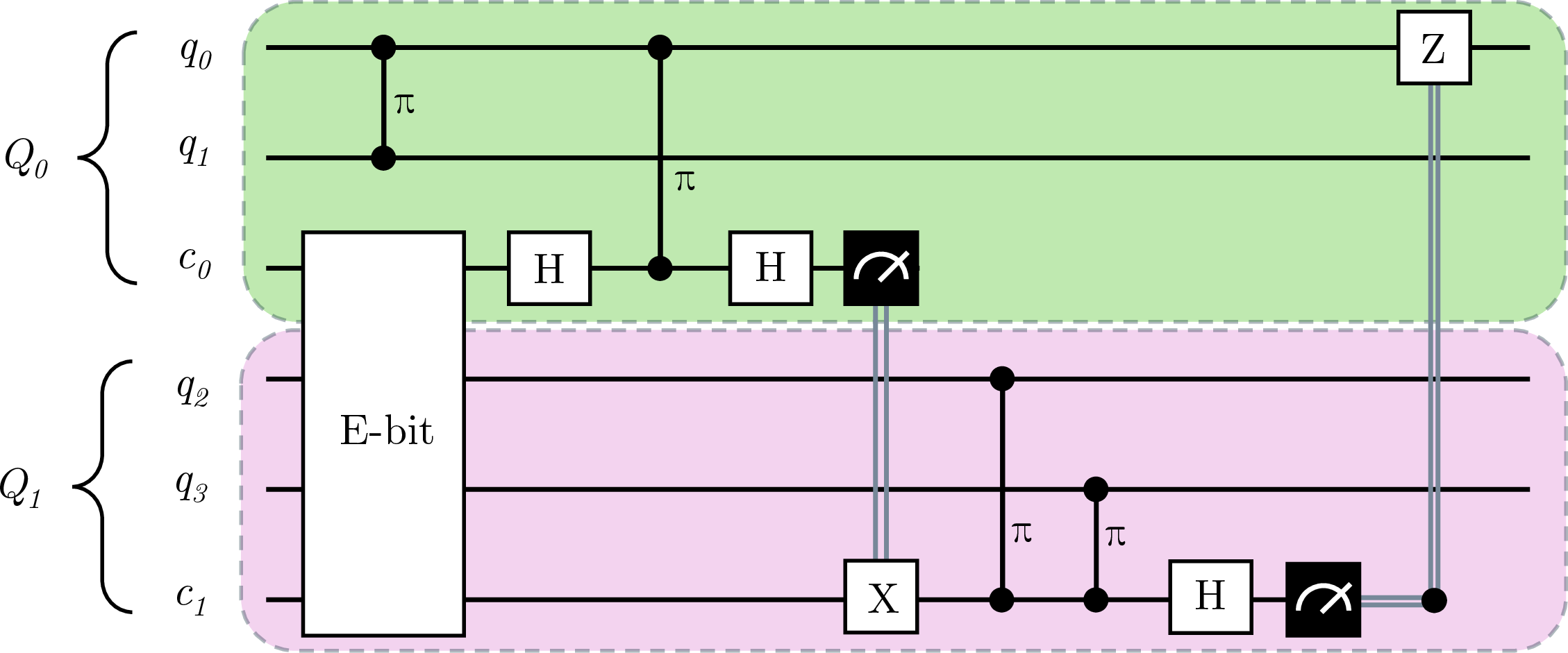
Figure 5: The circuit displays how two controlled-unitary gates can be teleported using the same e-bit.

The paper introduces two variants of the Generalized Circuit Partitioning approach: a simple variant (GCP-S) that considers regular gate teleportation and state teleportation, and an extended version (GCP-E) that incorporates gate packing mechanisms.

Generalised Circuit Partitioning - Simple (GCP-S)

GCP-S is built on an extended circuit interaction graph, characterized by nodes representing qubits at respective layers across a quantum circuit, creating edges that connect partner nodes during their interaction and additional edges for adjacent nodes representing the same qubit in successive layers. The graph includes the time-step number to balance e-bit cost with QPU local interaction compliance, ensuring all valid solutions (meeting QPU size constraints) can be explored systematically.

Generalised Circuit Partitioning - Extended (GCP-E)

GCP-E expands the simple variant approach to consider extended gate teleportation procedures, bundling groups of gates together for efficient distribution using shared e-bit resources. By generalizing the circuit partitioning problem, this approach manages to utilize the benefits of state teleportation for non-local operations while also leveraging extendable gate teleportation processes such as gate packing, thereby minimizing e-bit usage effectively. The greedy algorithm used for this extension always aims to add gates to the largest available group.

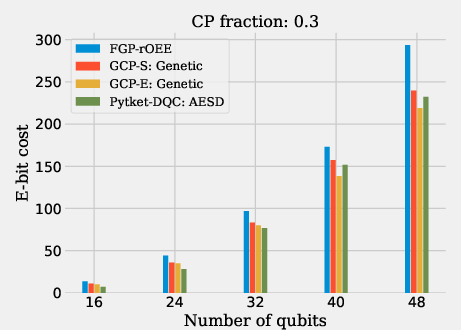
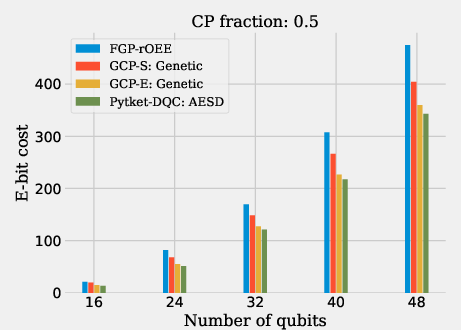
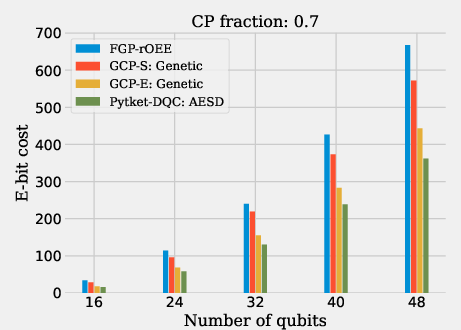
Figure 3: Results for random, CP fraction circuits.

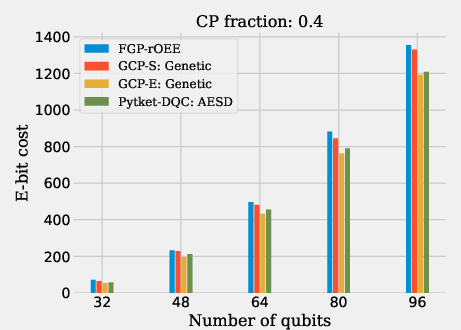
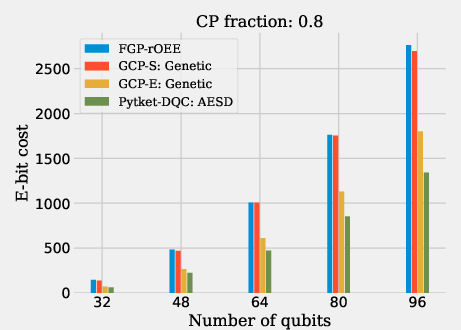
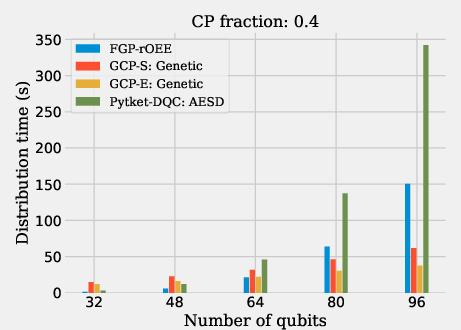
Figure 7: Results from larger CP fraction circuits distributed over QPUs consisting of 16 qubits each.

\section{Evaluation and Performance Metrics}

The evaluation was performed using various benchmark circuits, including CP fraction circuits, Quantum Fourier Transform (QFT), and Quantum Volume (QV) circuits. These benchmarks demonstrate the proposed Generalised Circuit Partitioning approaches: GCP-S (simple) and GCP-E (extended). Figures within the paper clearly show how different circuit partitioning techniques perform on these circuit types.

Figure 2: Random quantum circuit. See section \ref{sec:cp_frac}.

For CP fraction circuits (Figures 6 and 12), GCP-E achieves superior e-bit cost reduction, outperforming FGP-rOEE and AESD in instances where gate packing is plausible. In particular, on larger CP fraction circuits with a 0.7 fraction of two-qubit gates, GCP-E gives the lowest e-bit cost due to its unified approach of combining state and gate teleportation.

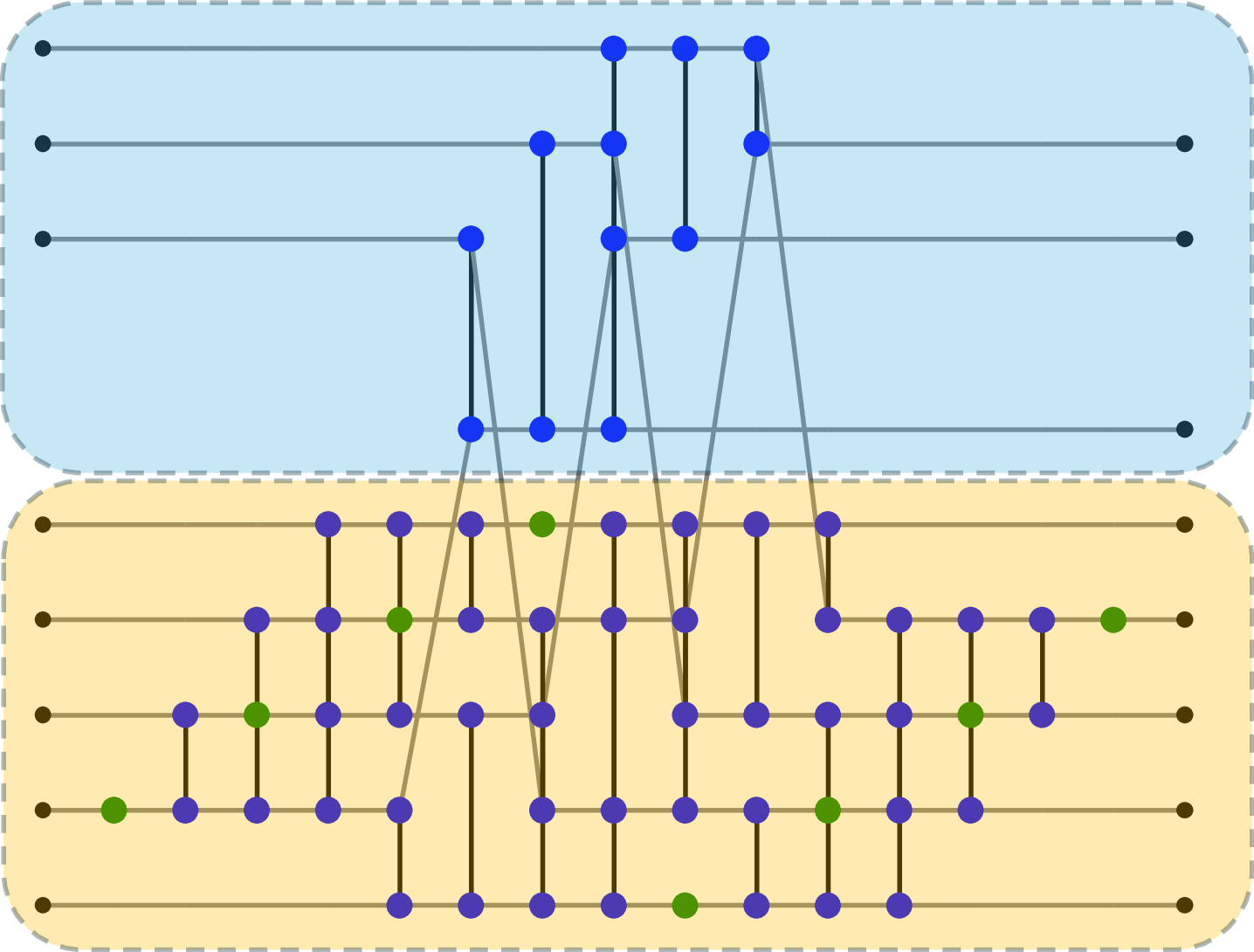
Figure 8: Simple optimisation. This is the same QFT as Figure 2, optimised using GCP-S, showing reduced usage of state teleportations.

Figure 3: State teleportation. This is the well known quantum teleportation procedure implemented using a controlled-phase gate rather than a CNOT.

For circuits such as QFT, where gate packing is naturally implied due to sequence structure, AESD exhibits superior performances as the extended gate teleportation methods are fully leveraged with no need for state teleportation.

\subsection{Scalability and Performance}

GCP-S provides improved e-bit costs on average, with the GCP-E variant marginally outperforming even advanced gate packing methods like AESD, while achieving this with much shorter compilation times. Figures display e-bit costs and computation time across different circuit types to highlight GCP's scalability, reflecting its linear computational complexity in relation to circuit size.

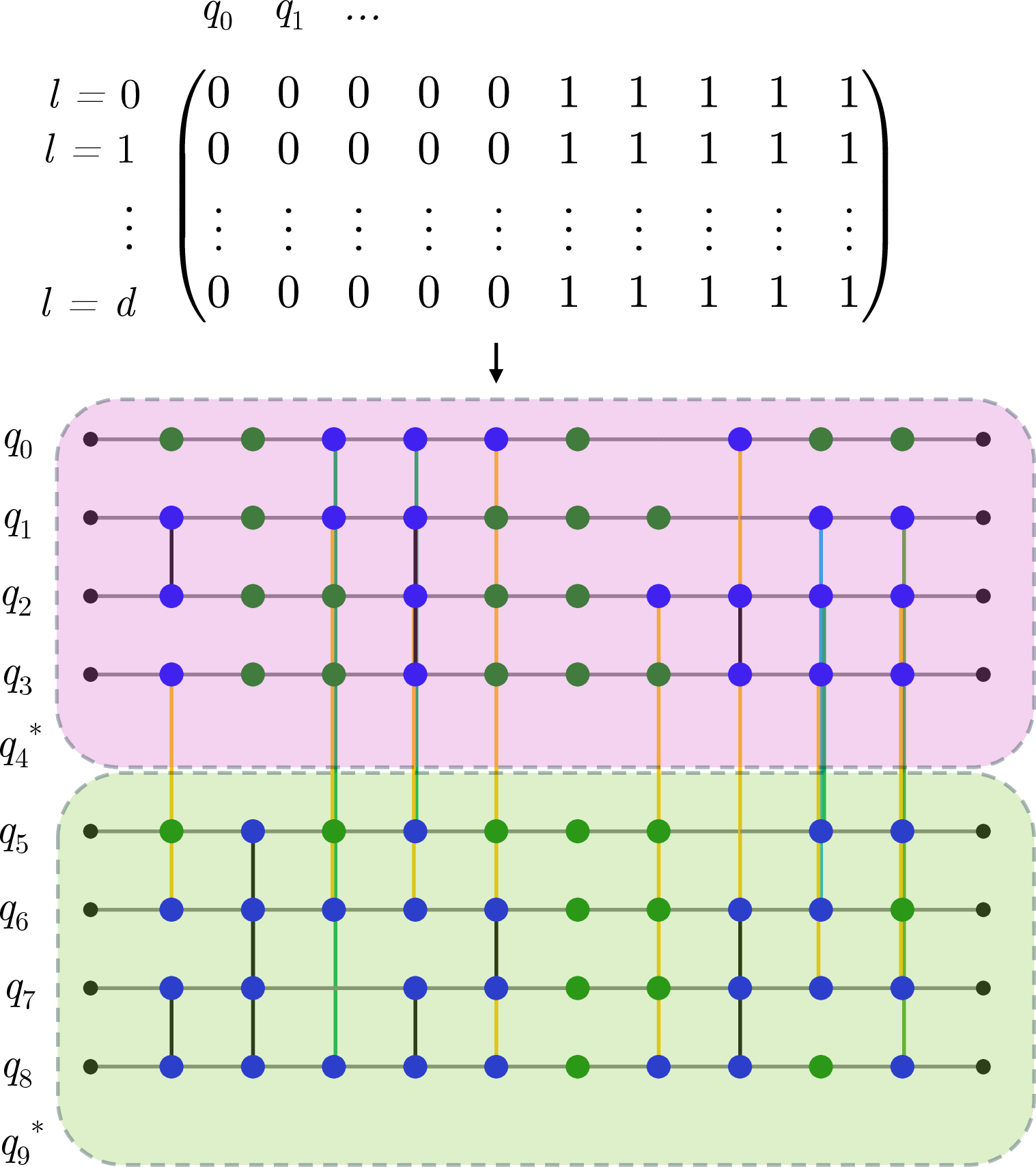
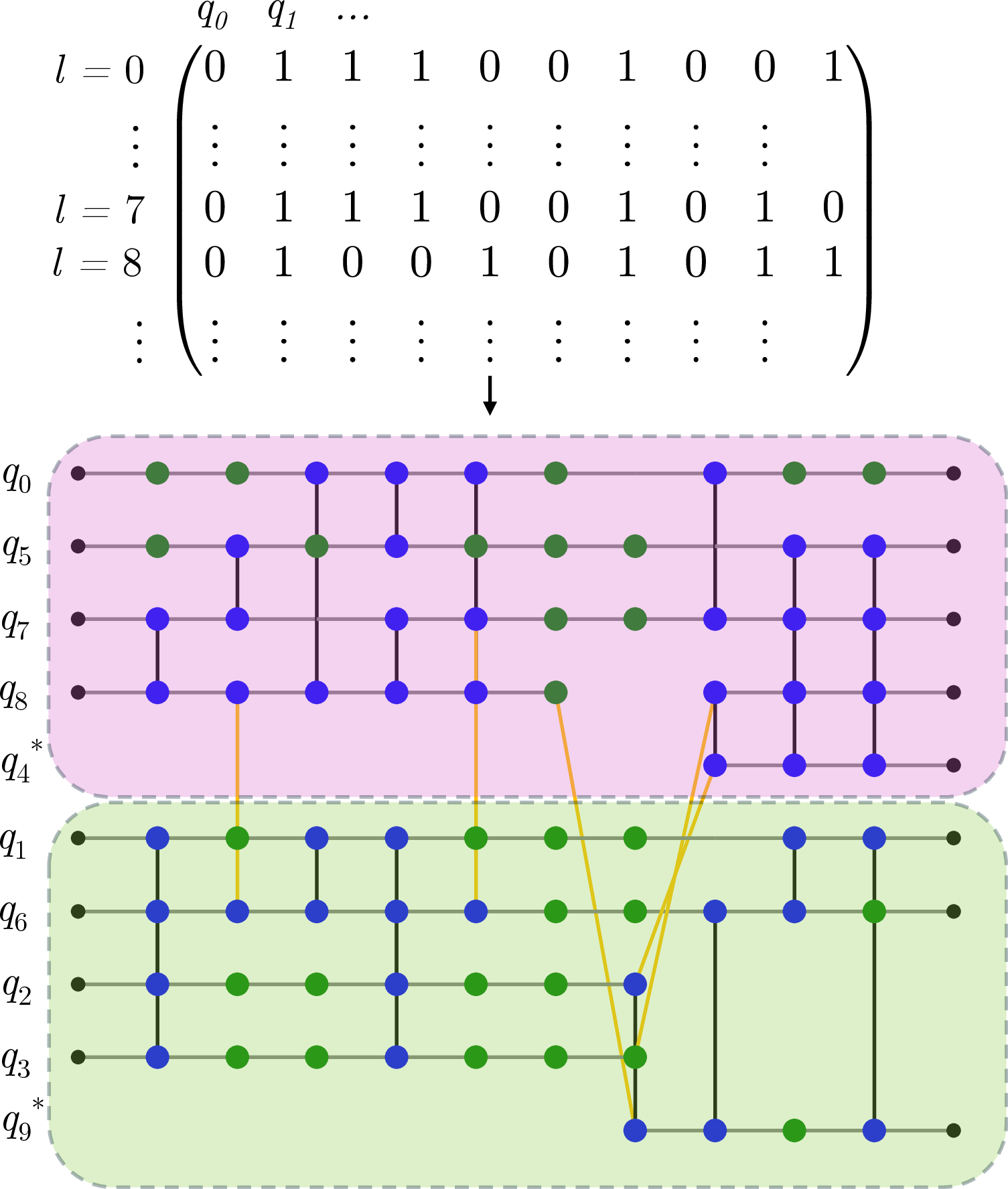
Figure 9: Visualising assignments on graphs. In a) we see the cost of a naive assignment, resulting in an e-bit cost of 13. In b) an optimised assignment sequence results in an e-bit cost of 5.

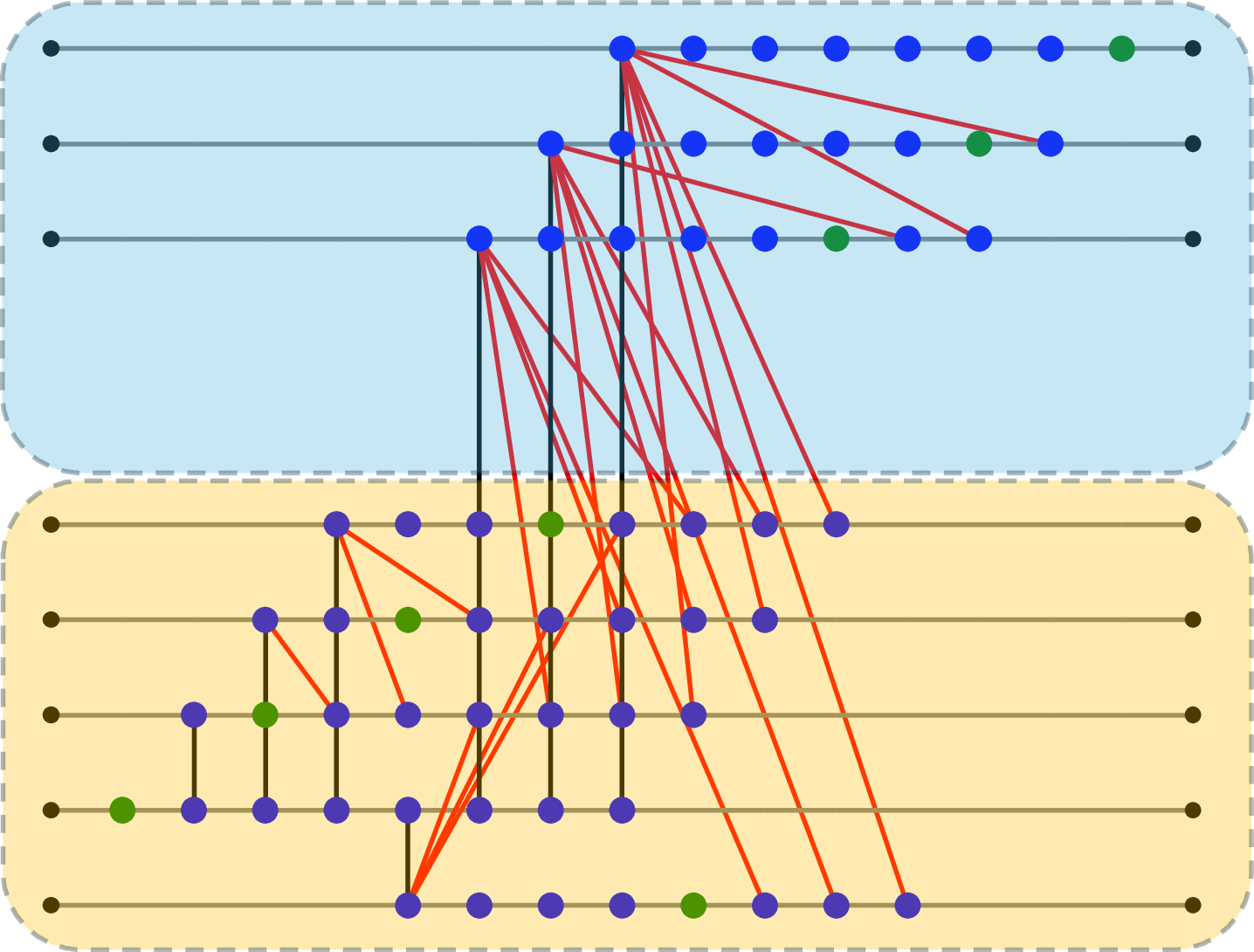
Figure 10: Extended optimisation. The Quantum Fourier Transform (QFT) circuit optimised using the GCP-E formulation showcases zero state teleportation requirement and an e-bit cost of 3.

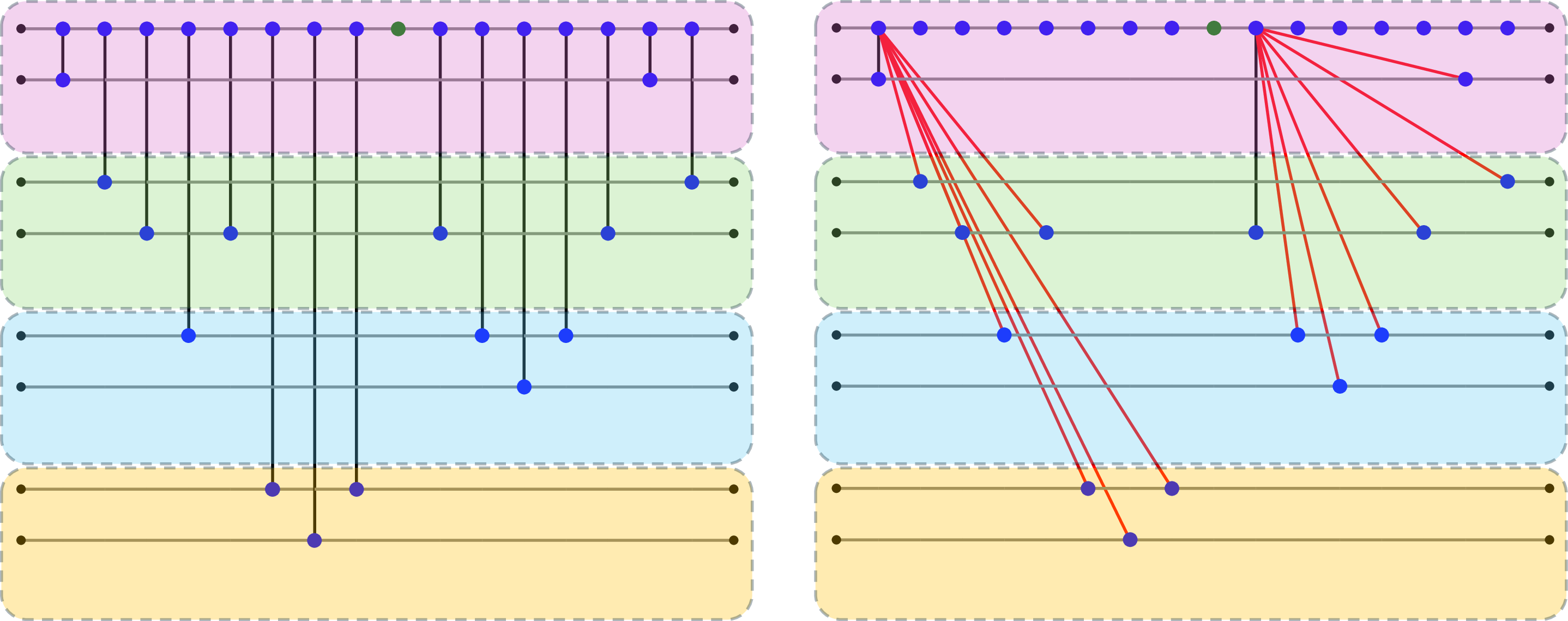
Figure 11: Gate grouping. All edges are merged onto the original control node. Since this node connects to three partitions outside its own, the e-bit cost for the assignment is 3.

\section{Conclusion}

The generalised circuit partitioning framework successfully proposes a coherent approach to the distribution of quantum circuits over multiple quantum processing units. Its ability to simultaneously exploit state and gate teleportation for circuit distribution offers a more cost-efficient and scalable alternative to current state-of-the-art methodologies. While methods like FGP-rOEE and AESD deliver low e-bit costs in specialized scenarios, they are constrained by their respective focus on a single type of teleportation, leading to inefficiencies in versatile circuit structures. The simple and extended versions of GCP introduce generalized models that cover both teleportation schemes, producing competitive e-bit performance with significantly reduced computation times, especially as circuit sizes increase. As development continues, the adaptation of GCP to accommodate general network topologies and distinct communication qubit constraints is anticipated. As distributed quantum systems become more prevalent, the comprehensive optimization strategies outlined in this paper could play a vital role in enhancing the efficiency and scalability of quantum computations.

Figure 11: All edges are merged onto the original control node. The assignment implies an e-bit cost of 3.

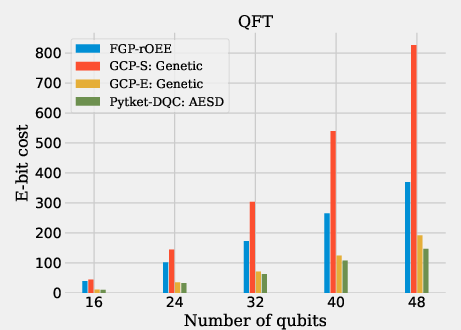
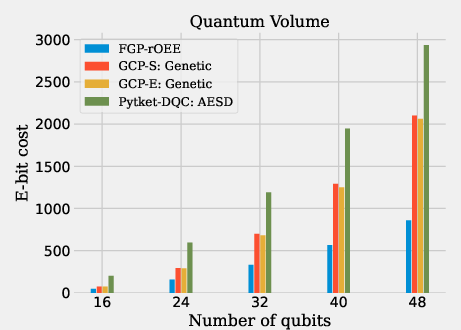
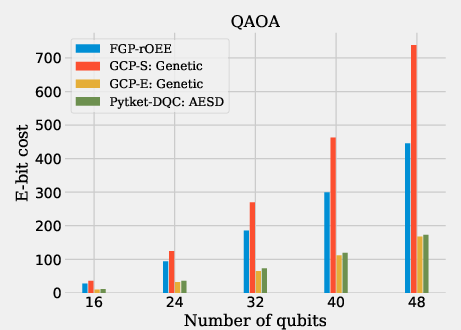
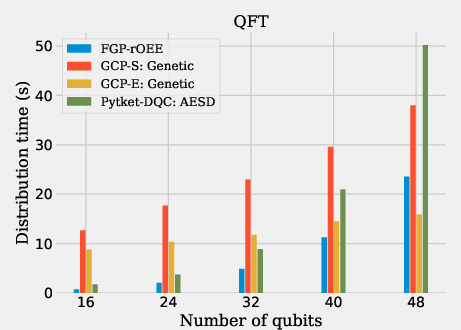
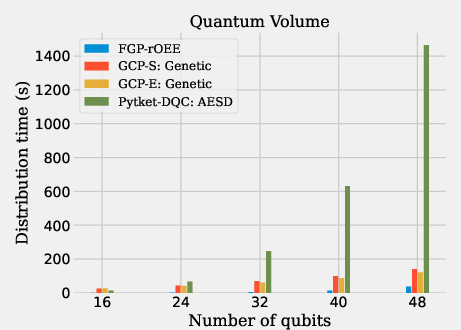
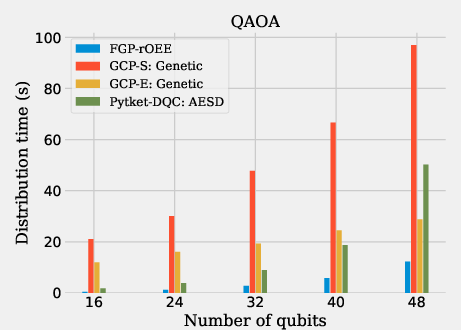
Figure 12: E-bit cost results.

Figure 6: Results for random, CP fraction circuits, as described in section \ref{sec:cp_frac}.

The research establishes that a more inclusive approach in quantum circuit partitioning significantly enhances the adaptability of algorithms to various circuit types, thereby reducing the average e-bit cost across diverse applications. These findings could have implications for optimizing DQC frameworks, addressing key hardware and algorithm challenges in quantum networks, potentially expediting the application of quantum computing to problems previously considered intractable.