Papers
Topics
Authors
Recent
2000 character limit reached

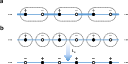
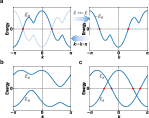
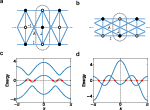
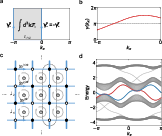
Revealing the spatial nature of sublattice symmetry (2404.11398v3)

Published 17 Apr 2024 in cond-mat.mes-hall, cond-mat.other, and cond-mat.str-el

Abstract: The sublattice symmetry on a bipartite lattice is commonly regarded as the chiral symmetry in the AIII class of the tenfold Altland-Zirnbauer classification. Here, we reveal the spatial nature of sublattice symmetry, and show that this assertion holds only if the periodicity of primitive unit cells agrees with that of the sublattice labeling. In cases where the periodicity does not agree, sublattice symmetry is represented as a glide reflection in energy-momentum space, which inverts energy and simultaneously translates some $k$ by $π$, leading to substantially different physics. Particularly, it introduces novel constraints on zero modes in semimetals and completely alters the classification table of topological insulators compared to class AIII. Notably, the dimensions corresponding to trivial and nontrivial classifications are switched, and the nontrivial classification becomes $\mathbb{Z}_2$ instead of $\mathbb{Z}$. We have applied these results to several models, including the Hofstadter model both with and without dimerization.

Definition Search Book Streamline Icon: https://streamlinehq.com
References (50)
  1. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
  2. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
  3. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
  4. Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys. Rev. B 55, 1142–1161 (1997).
  5. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
  6. Periodic table for topological insulators and superconductors. In AIP Conference Proceedings (AIP, 2009).
  7. Topological defects and gapless modes in insulators and superconductors. Phys. Rev. B 82, 115120 (2010).
  8. Classification of topological insulators and superconductors in the presence of reflection symmetry. Phys. Rev. B 88, 075142 (2013).
  9. Topological classification with additional symmetries from clifford algebras. Phys. Rev. B 88, 125129 (2013).
  10. Topological classification and stability of fermi surfaces. Phys. Rev. Lett. 110, 240404 (2013).
  11. Topological connection between the stability of fermi surfaces and topological insulators and superconductors. Phys. Rev. B 89, 075111 (2014).
  12. Topology of crystalline insulators and superconductors. Phys. Rev. B 90, 165114 (2014).
  13. Unified theory of p⁢t𝑝𝑡ptitalic_p italic_t and c⁢p𝑐𝑝cpitalic_c italic_p invariant topological metals and nodal superconductors. Phys. Rev. Lett. 116, 156402 (2016).
  14. Topology of nonsymmorphic crystalline insulators and superconductors. Phys. Rev. B 93, 195413 (2016).
  15. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).
  16. Chiral topological insulators, superconductors, and other competing orders in three dimensions. Phys. Rev. B 81, 045120 (2010).
  17. Band structure of a⁢b⁢c𝑎𝑏𝑐abcitalic_a italic_b italic_c-stacked graphene trilayers. Phys. Rev. B 82, 035409 (2010).
  18. Dirac and weyl superconductors in three dimensions. Phys. Rev. Lett. 113, 046401 (2014).
  19. Chiral topological insulating phases from three-dimensional nodal loop semimetals. Phys. Rev. B 95, 121107 (2017).
  20. Chiral topological insulator of magnons. Phys. Rev. B 97, 174413 (2018).
  21. Topology classification using chiral symmetry and spin correlations in graphene nanoribbons. Nano Lett. 21, 197–202 (2021).
  22. Manipulating topological edge spins in a one-dimensional optical lattice. Phys. Rev. Lett. 110, 076401 (2013).
  23. Topological boundary modes in isostatic lattices. Nature Physics 10, 39–45 (2014).
  24. Probe of three-dimensional chiral topological insulators in an optical lattice. Phys. Rev. Lett. 113, 033002 (2014).
  25. Yang, Z. et al. Topological acoustics. Phys. Rev. Lett. 114, 114301 (2015).
  26. Realizing and detecting a topological insulator in the aiii symmetry class. Phys. Rev. Lett. 119, 115301 (2017).
  27. Imhof, S. et al. Topolectrical-circuit realization of topological corner modes. Nature Physics 14, 925–929 (2018).
  28. Song, B. et al. Observation of symmetry-protected topological band with ultracold fermions. Science advances 4, eaao4748 (2018).
  29. Observation of higher-order topological acoustic states protected by generalized chiral symmetry. Nature materials 18, 113–120 (2019).
  30. Ji, W. et al. Quantum simulation for three-dimensional chiral topological insulator. Phys. Rev. Lett. 125, 020504 (2020).
  31. Xin, T. et al. Quantum phases of three-dimensional chiral topological insulators on a spin quantum simulator. Phys. Rev. Lett. 125, 090502 (2020).
  32. Shi, X. et al. Disorder-induced topological phase transition in a one-dimensional mechanical system. Phys. Rev. Res. 3, 033012 (2021).
  33. Topological acoustics. Nature Reviews Materials 7, 974–990 (2022).
  34. Geometry and topology tango in ordered and amorphous chiral matter. SciPost Physics 12, 038 (2022).
  35. Wang, D. et al. Realization of a ℤℤ\mathbb{Z}blackboard_Z-classified chiral-symmetric higher-order topological insulator in a coupling-inverted acoustic crystal. Phys. Rev. Lett. 131, 157201 (2023).
  36. Gauge-field extended k⋅p⋅𝑘𝑝k\cdot{}pitalic_k ⋅ italic_p method and novel topological phases. Phys. Rev. Lett. 127, 076401 (2021).
  37. Hofstadter, D. R. Energy levels and wave functions of bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).
  38. Winding number, family index theorem, and electron hopping in a magnetic field. Nuclear Physics B 316, 641–662 (1989).
  39. Time reversal polarization and a Z2subscript𝑍2{Z}_{2}italic_Z start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT adiabatic spin pump. Phys. Rev. B 74, 195312 (2006).
  40. Brillouin klein bottle from artificial gauge fields. Nature Communications 13, 2215 (2022).
  41. Z2subscript𝑍2{Z}_{2}italic_Z start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT topology in nonsymmorphic crystalline insulators: Möbius twist in surface states. Phys. Rev. B 91, 155120 (2015).
  42. 𝕫2subscript𝕫2{\mathbb{z}}_{2}blackboard_z start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT-projective translational symmetry protected topological phases. Phys. Rev. B 102, 161117 (2020).
  43. Nakahara, M. Geometry, topology and physics (CRC press, 2003).
  44. Symmetry and topology in non-hermitian physics. Phys. Rev. X 9, 041015 (2019).
  45. Non-hermitian topological invariants in real space. Phys. Rev. Lett. 123, 246801 (2019).
  46. Xiao, L. et al. Non-hermitian bulk–boundary correspondence in quantum dynamics. Nature Physics 16, 761–766 (2020).
  47. Chiral symmetry in non-hermitian systems: Product rule and clifford algebra. Phys. Rev. B 103, 014111 (2021).
  48. Hermitian topologies originating from non-hermitian braidings. Phys. Rev. B 108, 165105 (2023).
  49. Bulk-boundary correspondence of topological insulators from their respective green’s functions. Phys. Rev. B 84, 125132 (2011).
  50. Topological edge states with zero hall conductivity in a dimerized hofstadter model. Phys. Rev. Lett. 115, 216805 (2015).
Citations (1)
View on Semantic Scholar

Summary

  • The paper demonstrates that sublattice symmetry splits into two classes: Class I matching conventional chiral symmetry and Class II characterized by glide reflection.
  • It reclassifies zero mode counts and introduces a Z₂ topological invariant in even dimensions, refining conventional topological paradigms.
  • The study’s insights suggest new design principles for metamaterials, with potential applications in electronic, photonic, and non-Hermitian quantum systems.

Revealing the Spatial Nature of Sublattice Symmetry

Introduction

The paper, titled "Revealing the Spatial Nature of Sublattice Symmetry," examines the spatial properties of sublattice symmetries in bipartite lattices. It challenges the established notion that sublattice symmetry is synonymous with the chiral symmetry of the AIII class from the tenfold Altland-Zirnbauer classification. The authors reveal that this symmetry's nature significantly influences the topological classification of materials, especially when the periodicity of primitive unit cells does not align with sublattice labeling.

Sublattice Symmetries Classification

The paper categorizes sublattice symmetries into two distinct types:

  1. Class I Sublattice Symmetry: This adheres to conventional chiral symmetry, observed when the periodicity of the unit cells matches the sublattice labeling, as exemplified by the Su-Schrieffer-Heeger (SSH) model (Figure 1a).
  2. Class II Sublattice Symmetry: Here, a discrepancy between unit cell periodicity and sublattice labeling leads to sublattice symmetry exhibiting glide reflection in energy-momentum space. This unique representation demands reevaluation of conventional topological classifications. Figure 1

    Figure 1: Illustrations of (a) Class I and (b) Class II sublattice symmetries.

Implications for Zero Modes

By examining semimetals, the paper explores how Class II sublattice symmetries impose unique constraints on zero modes. Notably, when the glide reflection symmetry is expressed in band structures, it leads to zero mode counts that differ significantly depending on the configuration of states per unit cell. Figure 2

Figure 2: Two scenarios demonstrating glide reflection's effect on zero modes.

Topological Classification

Central to the findings is a revised topological classification table for class-II sublattice symmetry. Unlike the traditional Z\mathbb{Z} classification of chiral symmetry, Class II exhibits a Z2\mathbb{Z}_2 classification in even dimensions, swapping the roles of trivial and nontrivial classifications between even and odd dimensions.

This reclassification has profound implications, altering the established paradigms within topological insulators and semimetals and providing a new framework for understanding materials where internal and spatial symmetries intertwine. Figure 3

Figure 3: Band structures for semimetal models showing variations in zero mode counts.

Topological Invariants and Edge States

The paper derives new topological invariants from the band topology in systems exhibiting Class II sublattice symmetry. These invariants elucidate the conditions for protected edge states in two-dimensional systems. The invariant's formulation demonstrates intricate relations between Berry phases and glide reflection symmetries.

The application to dimerized Hofstadter models highlights the realization of these edge states, underscoring the practical relevance of the revised topological analysis for artificial lattice systems. Figure 4

Figure 4: Topological invariant configurations and corresponding edge state spectra.

Conclusion

The elucidation of the spatial nature of sublattice symmetry challenges and extends the existing framework of topological classification in condensed matter physics. The expansion from traditional chiral symmetry to incorporate spatially significant glide reflections broadens the detection and categorization of topological phases in both theoretical and experimental domains.

Looking forward, the relevance of class-II sublattice symmetry can elevate the design of metamaterials, with potential applications in robust electronic, photonic, and acoustic devices. Furthermore, explorations into non-Hermitian systems may further amplify the breadth and depth of this symmetry's applications in future quantum materials research.

File Document Download Save Streamline Icon: https://streamlinehq.com PDF File Document Download Save Streamline Icon: https://streamlinehq.com Markdown
Slide Deck Streamline Icon: https://streamlinehq.com

Whiteboard

Dice Question Streamline Icon: https://streamlinehq.com

Open Problems

We haven't generated a list of open problems mentioned in this paper yet.

Ai Sparkles Streamline Icon: https://streamlinehq.com Generate Now

Authors (2)

  1. Rong Xiao
  2. Y. X. Zhao
List To Do Tasks Checklist Streamline Icon: https://streamlinehq.com

Collections

Sign up for free to add this paper to one or more collections.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up
X Twitter Logo Streamline Icon: https://streamlinehq.com

Tweets

Sign up for free to view the 2 tweets with 7 likes about this paper.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up for Free