Inelastic tunneling through normal and superconducting junctions in the presence of photonic bath within Lindbladian formalism (2403.04441v2)

Abstract: An electron tunneling across a junction integrated into an electric circuit can generate an excitation in the photonic field (electromagnetic environment) and lose energy in the process. Such inelastic tunneling of particles is commonly described using the $P(E)$ theory. In the conventional approach to this theory, the tunneling rate and the electric current through the junction are derived using Fermi's golden rule and by averaging over the environmental photonic degrees of freedom. In this work, we address the same problem of inelastic tunneling due to photonic environment in Lindbladian formalism and we present how the photonic degrees of freedom are traced out in quantum master equation approach. The resulting quantum master equation is parameterized by the same $P(E)$ function and enables us to obtain not only the electric current but various other quantities, for instance the heat current, in a systematic and convenient way. We also demonstrate that the Lindbladian formalism provides a comprehensive description of Bogoliubov quasiparticle tunneling through superconducting junctions and that it properly accounts for the coherence factors. The coherence factors become important if the normal-state density of states is particle-hole asymmetric.

• The paper introduces a Lindbladian quantum master equation to advance beyond conventional P(E) theory for modeling inelastic tunneling.
• It systematically retains electronic variables while tracing out photonic degrees of freedom, enabling precise calculations of electric and heat currents.
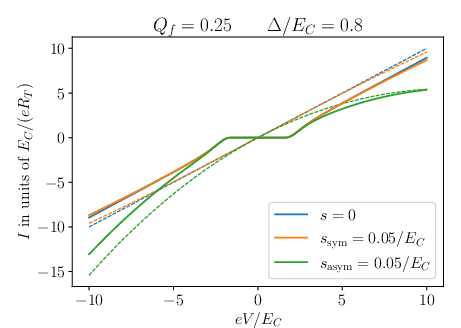
• Results demonstrate the method’s effectiveness in capturing symmetry-related effects in superconducting junctions through varying density-of-states.

Inelastic Tunneling Through Normal and Superconducting Junctions

The paper "Inelastic tunneling through normal and superconducting junctions in the presence of photonic bath within Lindbladian formalism" (2403.04441) explores a formalism for describing inelastic tunneling in electrical junctions. It employs a quantum master equation approach within the Lindbladian framework as an alternative to the conventional $P(E)$ theory, commonly using Fermi's golden rule. This approach traces out photonic degrees of freedom and retains all electronic variables, showcasing its utility in calculating quantities like electric and heat current systematically.

Quantum Tunneling and Lindbladian Formalism

Quantum Tunneling and Master Equation

Quantum tunneling, a non-classical phenomenon permitting particle transmission through potential barriers, critically influences electronic transport properties. The paper's primary focus is on deploying a quantum master equation under the Lindbladian formalism to expand the conventional $P(E)$ theory applications in inelastic tunneling.

• System Configuration: The paper models a tunnel junction embedded in a circuit where electrons can inelastically tunnel from one lead across the junction to another, interacting with the surrounding photonic bath (Figure 1). The circuit is characterized by its impedance $Z(\omega)$, bias voltage $V$, and junction capacitance $C$.

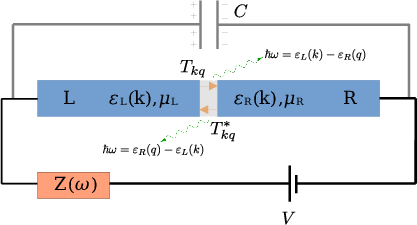
  Figure 1: Junction embedded into an electric circuit. Orange arrows indicate the possible tunneling processes through the insulating layer (grey). On the two sides of the junction, the left and the right leads are characterized by the energy spectra $\varepsilon_L(k)$ and $\varepsilon_R(q)$ and the chemical potentials of electrons, $\mu_{L/R}$.

Lindbladian vs. Conventional Approach

The Lindbladian formalism, unlike the $P(E)$ theory using Fermi's golden rule, traces out the photonic degrees of freedom while retaining electronic freedom levels. This framework reveals equivalencies in assumptions between the two approaches but maintains an advantage in computational adaptability by systematically obtaining various physical observables without further assumptions.

• Coherence Factors: Critical in scenarios with particle-hole asymmetry in normal-state density, coherence factors naturally emerge in the Lindbladian approach, providing a refined description of quasiparticle tunneling through superconducting junctions.

Application and Results

Superconducting Junction Analysis

A demonstration of practical application in superconducting junctions reveals the efficiency of the Lindbladian approach. The paper contrasts scenarios with different types of density of states, highlighting how particle-hole symmetry impacts the $I(V)$ characteristics.

• Symmetric and Asymmetric Cases: For symmetric densities, uniform $I(V)$ characteristics are evident. However, anti-symmetric cases exhibit distinctive behaviors due to broken particle-hole symmetry.

  Figure 2: I(V) characteristics for different types of density of states, comparing uniform density with symmetric and anti-symmetric cases.

Impact on Computational and Experimental Design

The results indicate potential improvements in computational schemes for complex systems with electronic interactions. Particularly, incorporating this formalism can extend to involving additional processes, such as quasiparticle tunnelling and dissipative interactions, providing a better foundation for designing thermodynamic and transport experiments in novel superconductive materials.

Conclusion

The Lindbladian approach expands the conventional $P(E)$ framework by providing a systematic method to compute various tunnelling phenomena observables. It highlights the coherence factors' significance in scenarios with broken symmetry in superconducting leads, offering potential advancements in understanding inelastic tunneling mechanisms. The methodological flexibility and deeper insight this formalism provides make it a valuable tool for analyzing complex quantum systems. Future studies could extend this approach to include more involved systems, such as those with impurities or interacting quasiparticles.