Equivariant neural network for Green's functions of molecules and materials (2312.14680v2)
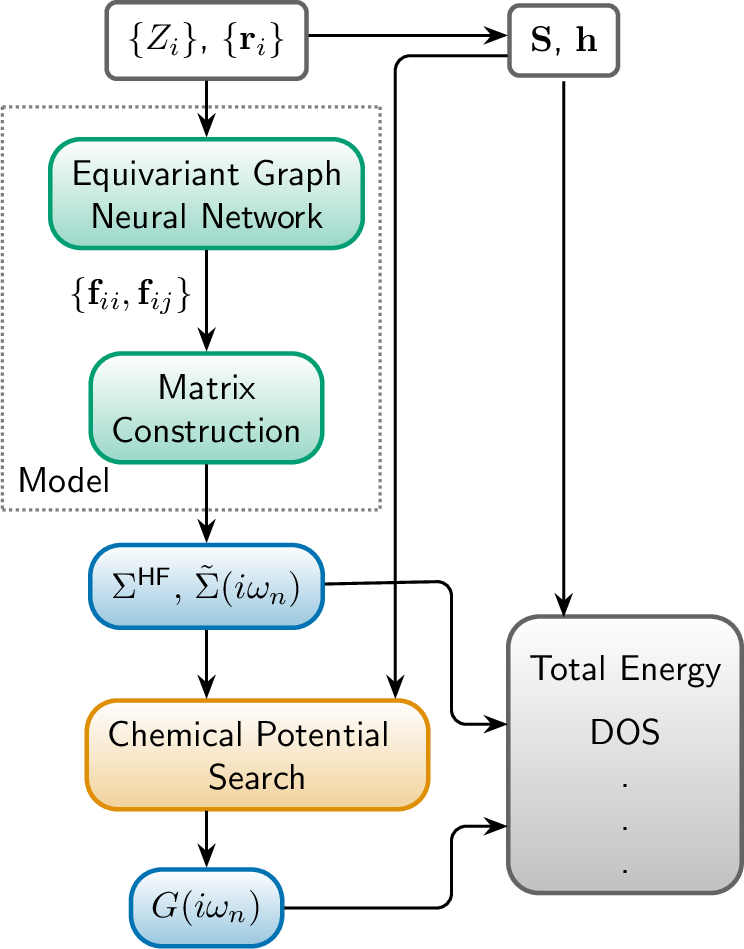
Abstract: The many-body Green's function provides access to electronic properties beyond density functional theory level in ab inito calculations. In this manuscript, we propose a deep learning framework for predicting the finite-temperature Green's function in atomic orbital space, aiming to achieve a balance between accuracy and efficiency. By predicting the self-energy matrices in Lehmann representation using an equivariant message passing neural network, our method respects its analytical property and the $E(3)$ equivariance. The Green's function is obtained from the predicted self-energy through Dyson equation with target total number of electrons. We present proof-of-concept benchmark results for both molecules and simple periodic systems, showing that our method is able to provide accurate estimate of physical observables such as energy and density of states based on the predicted Green's function.
- N. E. Dahlen and R. van Leeuwen, Self-consistent solution of the dyson equation for atoms and molecules within a conserving approximation, The Journal of Chemical Physics, The Journal of Chemical Physics 122, 164102 (2005).
- D. Zgid and G. K.-L. Chan, Dynamical mean-field theory from a quantum chemical perspective, The Journal of Chemical Physics 134, 094115 (2011), https://pubs.aip.org/aip/jcp/article-pdf/doi/10.1063/1.3556707/13306596/094115_1_online.pdf .
- T. N. Lan, A. A. Kananenka, and D. Zgid, Communication: Towards ab initio self-energy embedding theory in quantum chemistry, The Journal of Chemical Physics 143, 241102 (2015), https://pubs.aip.org/aip/jcp/article-pdf/doi/10.1063/1.4938562/15506742/241102_1_online.pdf .
- T. Zhu, Z.-H. Cui, and G. K.-L. Chan, Efficient formulation of ab initio quantum embedding in periodic systems: Dynamical mean-field theory, Journal of Chemical Theory and Computation 16, 141 (2020).
- A. Shee and D. Zgid, Coupled cluster as an impurity solver for green’s function embedding methods, Journal of Chemical Theory and Computation 15, 6010 (2019).
- O. J. Backhouse and G. H. Booth, Efficient excitations and spectra within a perturbative renormalization approach, Journal of Chemical Theory and Computation 16, 6294 (2020).
- S. J. Bintrim and T. C. Berkelbach, Full-frequency GW without frequency, The Journal of Chemical Physics 154, 041101 (2021), https://pubs.aip.org/aip/jcp/article-pdf/doi/10.1063/5.0035141/13941773/041101_1_online.pdf .
- X. Dong, E. Gull, and H. U. R. Strand, Excitations and spectra from equilibrium real-time green’s functions, Phys. Rev. B 106, 125153 (2022).
- M. Geiger and T. Smidt, e3nn: Euclidean neural networks (2022), arXiv:2207.09453 [cs.LG] .
- J. W. Negele and H. Orland, Quantum Many-particle Systems (Addison-Wesley, 1988).
- A. Szabo and N. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover Books on Chemistry (Dover Publications, 1996).
- G. Mahan, Many-Particle Physics, Physics of Solids and Liquids (Springer US, 2012).
- G. Stefanucci and R. van Leeuwen, Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction (Cambridge University Press, 2013).
- J. M. Luttinger and J. C. Ward, Ground-state energy of a many-fermion system. ii, Phys. Rev. 118, 1417 (1960).
- N. E. Dahlen, R. van Leeuwen, and U. von Barth, Variational energy functionals of the green function and of the density tested on molecules, Phys. Rev. A 73, 012511 (2006).
- J. J. Phillips and D. Zgid, Communication: The description of strong correlation within self-consistent green’s function second-order perturbation theory, The Journal of Chemical Physics, The Journal of Chemical Physics 140, 241101 (2014).
- A. A. Rusakov and D. Zgid, Self-consistent second-order green’s function perturbation theory for periodic systems, The Journal of Chemical Physics 144, 054106 (2016).
- A. R. Welden, A. A. Rusakov, and D. Zgid, Exploring connections between statistical mechanics and green’s functions for realistic systems: Temperature dependent electronic entropy and internal energy from a self-consistent second-order green’s function, The Journal of Chemical Physics 145, 204106 (2016).
- J. Gasteiger, J. Groß, and S. Günnemann, Directional message passing for molecular graphs, in International Conference on Learning Representations (2020).
- J. Fei, C.-N. Yeh, and E. Gull, Nevanlinna analytical continuation, Phys. Rev. Lett. 126, 056402 (2021a).
- B. Farid, On the luttinger-ward functional and the convergence of skeleton diagrammatic series expansion of the self-energy for hubbard-like models (2021), arXiv:2108.10903 [cond-mat.str-el] .
- C. Gramsch and M. Potthoff, Lehmann representation of the nonequilibrium self-energy, Phys. Rev. B 92, 235135 (2015).
- N. Akhiezer, The Classical Moment Problem: And Some Related Questions in Analysis, University mathematical monographs (Oliver and Boyd, 1965).
- J. Kaye, K. Chen, and O. Parcollet, Discrete lehmann representation of imaginary time green’s functions, Phys. Rev. B 105, 235115 (2022a).
- J. Kaye, K. Chen, and H. U. Strand, libdlr: Efficient imaginary time calculations using the discrete lehmann representation, Computer Physics Communications 280, 108458 (2022b).
- J. J. Phillips, A. A. Kananenka, and D. Zgid, Fractional charge and spin errors in self-consistent Green’s function theory, Journal of Chemical Physics 142, 194108 (2015).
- N. Chikano, J. Otsuki, and H. Shinaoka, Performance analysis of a physically constructed orthogonal representation of imaginary-time green’s function, Phys. Rev. B 98, 035104 (2018).
- Green, green-phys.org.
- S. Passaro and C. L. Zitnick, Reducing so(3) convolutions to so(2) for efficient equivariant gnns, in Proceedings of the 40th International Conference on Machine Learning, ICML’23 (JMLR.org, 2023).
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Collections
Sign up for free to add this paper to one or more collections.