Safe Importance Sampling in Model Predictive Path Integral Control

Abstract: We introduce the notion of importance sampling under embedded barrier state control, titled Safety Controlled Model Predictive Path Integral Control (SC-MPPI). For robotic systems operating in an environment with multiple constraints, hard constraints are often encoded utilizing penalty functions when performing optimization. Alternative schemes utilizing optimization-based techniques, such as Control Barrier Functions, can be used as a safety filter to ensure the system does not violate the given hard constraints. In contrast, this work leverages the principle of a safety filter but applies it during forward sampling for Model Predictive Path Integral Control. The resulting set of forward samples can remain safe within the domain of the safety controller, increasing sample efficiency and allowing for improved exploration of the state space. We derive this controller through information theoretic principles analogous to Information Theoretic MPPI. We empirically demonstrate both superior sample efficiency, exploration, and system performance of SC-MPPI when compared to Model-Predictive Path Integral Control (MPPI) and Differential Dynamic Programming (DDP) optimizing the barrier state.

• The paper introduces SC-MPPI, a model predictive path integral control method that integrates barrier state feedback to enforce safety constraints.
• It modifies the MPPI cost function to minimize unsafe trajectories, optimizing control inputs for improved sampling efficiency.
• Empirical results on Dubins vehicles and quadrotors demonstrate higher task completion rates, lower RMSE, and robust navigation in complex environments.

Implementation of Safe Importance Sampling in Model Predictive Path Integral Control

Introduction

The paper presents "Safe Importance Sampling in Model Predictive Path Integral Control (SC-MPPI)", introducing a novel approach for ensuring safety in robotic navigation through constrained environments. It addresses the challenge of dynamic systems maintaining safety constraints, often handled through control barrier functions (CBFs) or penalty methods. The focus is on integrating safety as a fundamental element of the sampling process in the Model Predictive Path Integral Control (MPPI) framework.

Figure 1: Quadrotor in a dense obstacle field with visualization of the sampling. Safe samples are shown in blue, and unsafe samples are in red.

Safe Importance Sampling Framework

The key contribution of the paper is an integration of barrier state feedback control into the sampling methodology of MPPI. The SC-MPPI framework embeds the safety mechanisms directly into the sampling phase by leveraging differential dynamic programming (DDP) with Discrete Barrier States (DBaS). This establishes forward invariance of safe spaces, thereby keeping the system trajectories within predefined safe boundaries.

The core of the framework is the derivation of a controller capable of dynamically enforcing these safety constraints while maintaining efficiency and exploration capabilities. The proposed method modifies the standard MPPI cost function to account for the distribution of control inputs in such a way that unsafe samples are minimized.

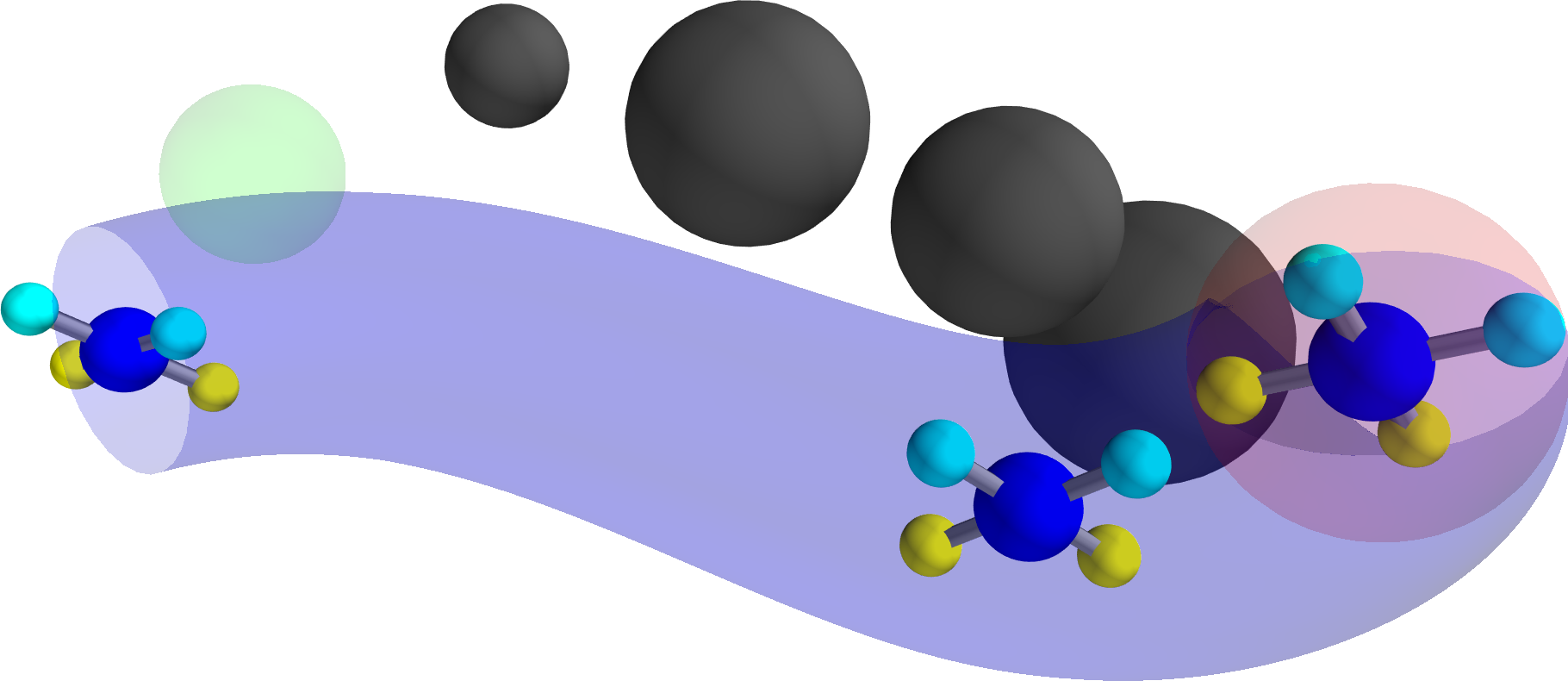
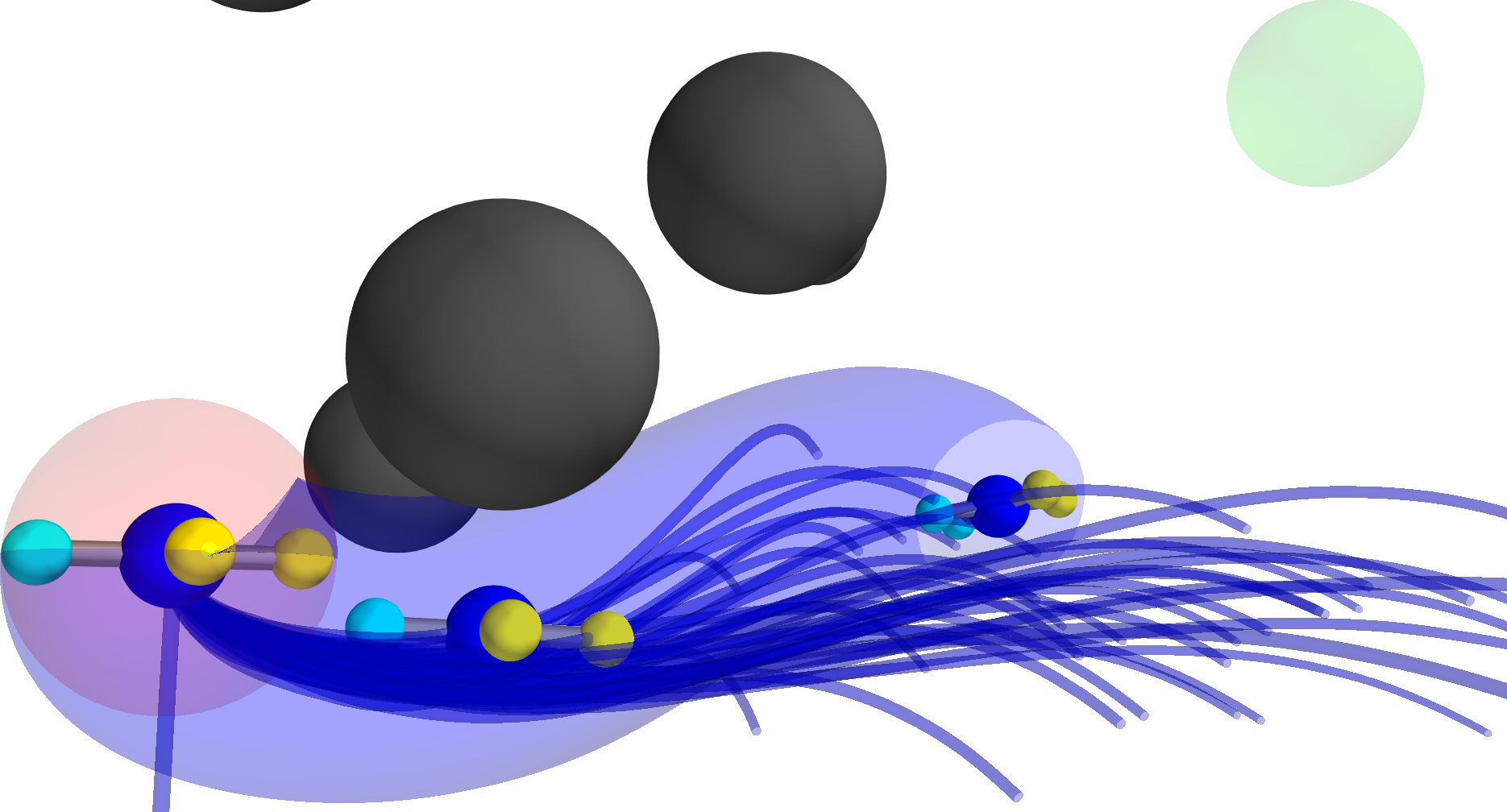
Figure 2: The proposed importance sampling scheme with a red unsafe reference trajectory, a blue corrected safe trajectory, and safe samples under barrier state feedback.

Mathematical Formulation

Fundamentally, SC-MPPI builds upon the definition of importance sampling by embedding barrier state feedback to redefine potential risk areas in the path integral control setting. The control law in SC-MPPI augments the cost function by considering the discrete barrier's dynamics, ensuring that unsafe trajectories exponentially decrease and, hence, contribute less to the importance sampling.

The model defines a safe set $C$ within which trajectories are dynamically enforced through barrier state-based control laws, ensuring that each sampled path respects the imposed safety constraints. This is achieved through iterative refinement, where the control distribution $Q^*$ is optimized under these modified safety constraints, as illustrated in the algorithms outlined in the paper.

Empirical Results

Empirical evaluations demonstrate the superior performance of SC-MPPI compared to standard MPPI and other robust control techniques such as Model Predictive Differential Dynamic Programming (MPC-DDP). Two key experiments highlight SC-MPPI's effectiveness: navigation tasks for a Dubins vehicle and a quadrotor system.

In these experiments, SC-MPPI showcases greater sample efficiency and system performance, maintaining safety with higher success rates in complex environments. Metrics such as task completion, average trajectory speed, and proximity to obstacles validate these claims, with SC-MPPI achieving higher task completion percentages and lower root mean square errors (RMSE) in positioning compared to baseline methods.

Figure 3: Dubins vehicle samples with safe samples in blue, and unsafe samples in red, showing SC-MPPI's deflection around obstacles.

Conclusion

The paper introduces a significant refinement to the MPPI framework by integrating safety at the sampling level. SC-MPPI empowers real-time systems to uphold safety constraints dynamically without substantial computational overhead, as shown in the experiments. The approach addresses essential gaps in safety-critical applications, offering a robust control paradigm with broader implications for various domains needing stringent safety adherence.

Future work may address the algorithm's sensitivity to parameter tuning and explore its scalability in even more extensive and challenging environments. This methodology sets the stage for refining sampling-based control strategies, potentially leading to new avenues in autonomous systems' safe exploration and navigation.