Optimal intercellular competition in senescence and cancer (2211.03312v2)

Abstract: Effective multicellularity requires both cooperation and competition between constituent cells. Cooperation involves sacrificing individual fitness in favor of that of the community, but excessive cooperation makes the community susceptible to senescence and aging. Competition eliminates unfit senescent cells via natural selection and thus slows down aging, but excessive competition makes the community susceptible to cheaters, as exemplified by cancer and cancer-like phenomena. These observations suggest that an optimal level of intercellular competition in a multicellular organism maximizes organismal vitality by delaying the inevitability of aging. We quantify this idea using a statistical mechanical framework that leads to a generalized replicator dynamical system for the population of cells that change their vitality and cooperation due to somatic mutations that make them susceptible to aging and/or cancer. By accounting for the cost of cooperation and strength of competition in a minimal setting, we show that our model predicts an optimal value of competition that maximizes vitality and delays the inevitability of senescence or cancer.

• The paper introduces a replicator dynamical system to model cell vigor and cooperation in aging and cancer.
• It demonstrates that optimal intercellular competition delays senescence and mitigates cancer proliferation.
• The study reveals a phase shift where mutation-driven dynamics transition from rapid senescence to slower cancerous transformations.

Optimal Intercellular Competition in Senescence and Cancer

This study addresses the delicate balance between intercellular cooperation and competition within multicellular organisms, focusing on their implications for senescence and cancer development. The authors approach this from a statistical mechanics perspective, introducing a generalized replicator dynamical system to model cell populations' vitality, affected by somatic mutations.

Theoretical Framework and Model Development

The paper presents a model where cell types within an organism are characterized by two traits: vigor ($v$) and cooperation ($c$), forming a two-dimensional state space. Vigor represents cell resources or metabolic activity, while cooperation reflects resource allocation towards organismal functions. Mutations affect these traits, deregulating this balance and contributing to aging and cancer.

The model employs a master equation akin to the Price equation, integrating both proliferation and mutation dynamics in a replicator-like framework:

$$\frac{\partial N(v,c,t)}{\partial t} = \text{Growth} + \text{Mutation Fluxes}$$

Here, $N(v,c,t)$ represents the population of cells in state $(v,c)$ at time $t$, while the growth component is driven by a state-dependent fitness function $f(v,c)$.

Figure 1: Master equation for multicellular aging.

Dynamical Analysis of Cell Populations

The authors explore the time evolution of cell populations under their proposed framework. They reveal that the dynamics exhibit two distinct phases: a rapid accumulation of senescent cells followed by a slower phase dominated by cancerous transformations. The model captures the interplay between mutation dynamics and competitive proliferation, suggesting the existence of an optimal competition level.

Figure 2: Dynamics of multicellular aging.

Organismal Vitality and Optimal Competition

The study constructs an expression for organismal vitality, $\overline{V}(t)$, as a function of cell vigor and cooperation, weighted by their respective population fractions. The non-monotonic relationship between vitality and competition strength suggests an optimal value $f_0^\star$ that significantly enhances vitality.

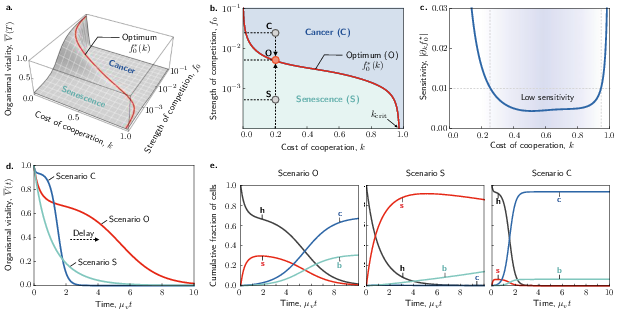
Figure 3: Organismal vitality and optimal competition.

The findings indicate that too little competition leads to senescent cell accumulation, whereas excessive competition exacerbates cancer proliferation, highlighting the necessity for a balanced competitive environment.

Implications and Future Directions

This work has far-reaching implications for understanding aging and designing interventions in both biological and synthetic systems. By suggesting an optimal level of intra-organismal competition, it offers a potential framework for strategies aimed at delaying senescence and managing cancer dynamics.

Experimental validation of the model in biological settings could help refine these optimal parameters. Future research could also explore how feedback mechanisms between competition and system state impact long-term organismal vitality.

Conclusion

This paper presents a statistical mechanical approach to modeling multicellular aging, emphasizing the intricate balance between intercellular competition and cooperation. The derived optimal competition level provides valuable insights for potential interventions in senescence and cancer management, encouraging further exploration of its applicability across various domains.