Post-Training Quantization for Cross-Platform Learned Image Compression

Abstract: It has been witnessed that learned image compression has outperformed conventional image coding techniques and tends to be practical in industrial applications. One of the most critical issues that need to be considered is the non-deterministic calculation, which makes the probability prediction cross-platform inconsistent and frustrates successful decoding. We propose to solve this problem by introducing well-developed post-training quantization and making the model inference integer-arithmetic-only, which is much simpler than presently existing training and fine-tuning based approaches yet still keeps the superior rate-distortion performance of learned image compression. Based on that, we further improve the discretization of the entropy parameters and extend the deterministic inference to fit Gaussian mixture models. With our proposed methods, the current state-of-the-art image compression models can infer in a cross-platform consistent manner, which makes the further development and practice of learned image compression more promising.

• The paper proposes post-training quantization to enforce integer-only inference, eliminating cross-platform inconsistencies in learned image compression.
• It employs uniform affine quantization and a controlled requantization process with dyadic multiplication to safeguard error-free 32-bit integer computation.
• The study demonstrates negligible rate-distortion losses and enhanced hardware efficiency, validating the method's practical deployment across diverse neural architectures.

Post-Training Quantization for Cross-Platform Learned Image Compression

Introduction

The paper introduces a method for addressing the non-deterministic nature of learned image compression across different platforms. Non-deterministic behavior, stemming from floating-point arithmetic in model inference, leads to inconsistencies in probability prediction, thwarting successful cross-platform decoding. The authors propose utilizing post-training quantization (PTQ) to enforce integer-arithmetic-only inference, maintaining superior rate-distortion performance without complex training or fine-tuning.

Figure 1: The cross-platform inconsistency caused by non-deterministic model inference.

Methodology

Integer-Arithmetic-Only Inference

To achieve consistent cross-platform inference, the paper enforces integer-only arithmetic by applying PTQ. This involves uniform affine quantization (UAQ) to convert both model weights and activations to fixed-point numbers, utilizing integer matrix multiplications. The requisite step is ensuring computations rely solely on 32-bit integers, deterring any device-specific operations.

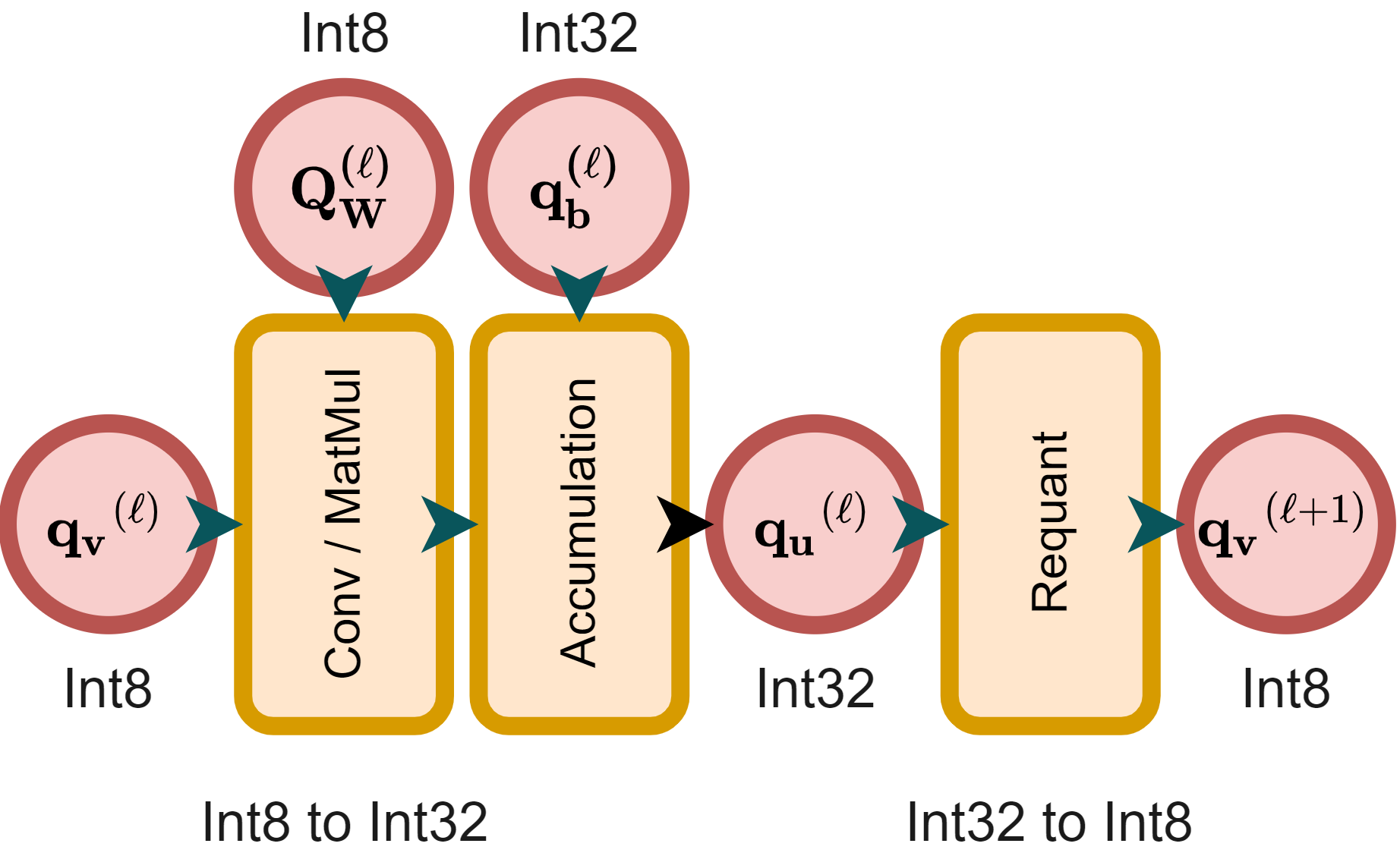
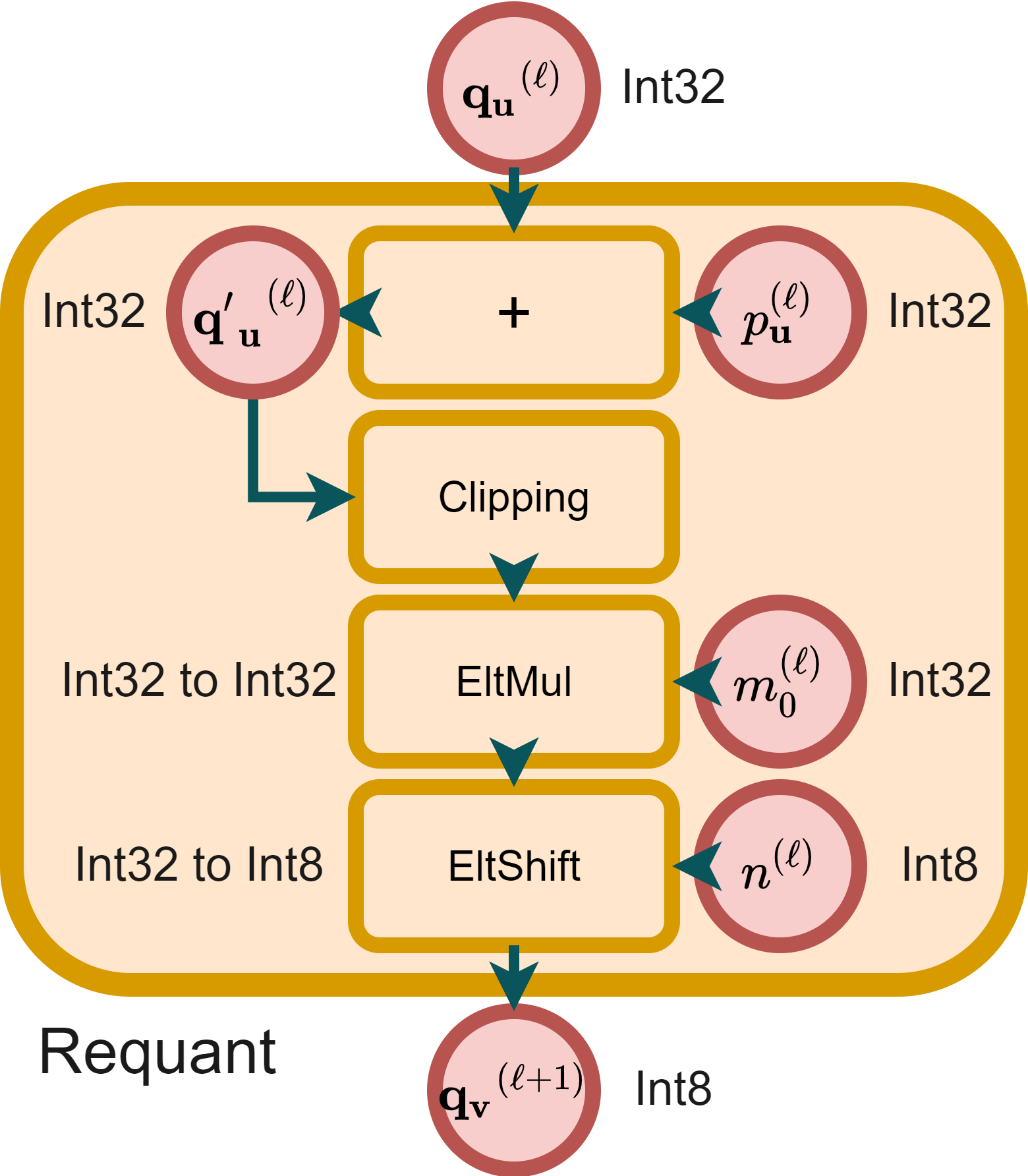
Figure 2: The integer-arithmetic-only inference using offline-constrained integer-arithmetic-only requantization.

Requantization

The requantization process between linear layers features dyadic multiplication, previously risk-prone due to potential overflow in fixed-point quantization. By tightly constraining the requantization process using pre-scaling zero-point and offline calculation of dyadic numbers, the approach guarantees error-free 32-bit integer multiplication, ensuring platform-independent consistent computation.

Parameter Discretization

Parameter discretization is a pivotal aspect for creating lookup tables (LUTs) required for entropy coding. The authors introduce a binary logarithm-based standard deviation (STD) discretization to ensure hardware efficiency and non-determinism avoidance. Compared to prior methods using natural logarithm discretization, the binary approach involves 65-level binary-logarithmic sampling with linear interpolation, significantly enhancing computational efficiency.

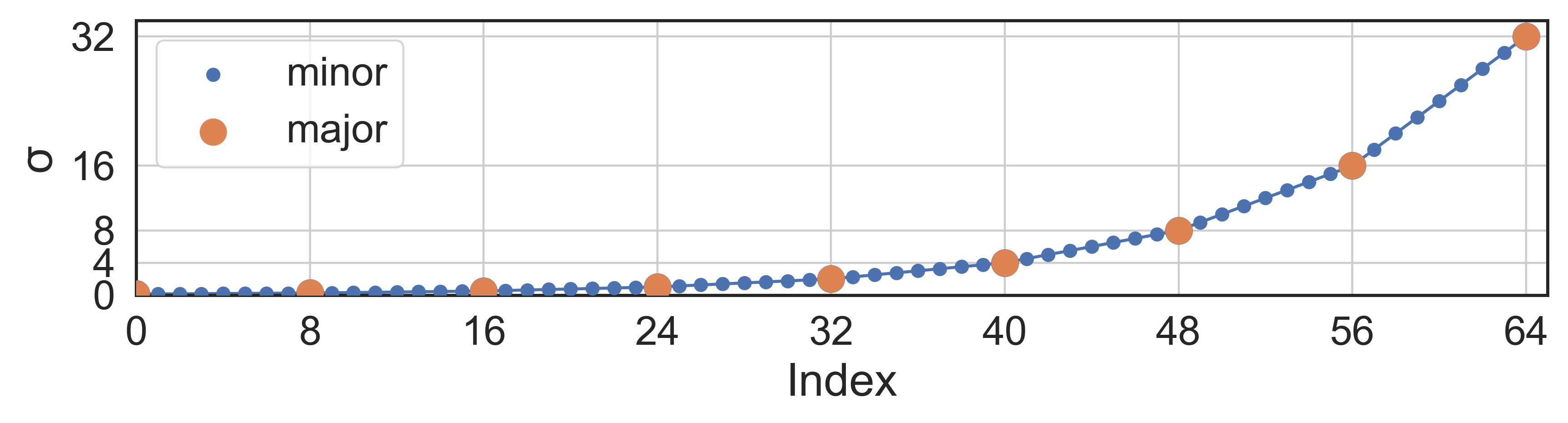
Figure 3: Visualization of the proposed 65-level STD parameter discretization.

Experiments

Encoded using codec models like \citep{minnen2018joint} and \citep{cheng2020learned}, experiments show that implementing PTQ results in negligible degradation in rate-distortion performance across various network architectures. The RD performance with integer-arithmetic-only inference closely matches that of original floating-point models, as evidenced by the Bjøntegaard Delta-rate metric demonstrating minor increases.

Figure 4: RD curves evaluated on Kodak showing marginal differences in compression performance with integer-arithmetic-only models.

Results and Discussion

Compression Performance

The empirically tested models demonstrate that PTQ can accurately infer rate-distortion metrics with insignificant losses, even surpassing alternative quantization approaches. By eliminating errors during entropy parameter computation, the method helps to achieve a near-zero cross-platform decoding error rate.

Discretization Efficiency

The binary logarithm STD discretization notably accelerates inference latency, demonstrating improved calibration on high-resolution images compared to traditional comparison methodologies, emphasizing the practical feasibility of this method.

Conclusion

The research illustrates that leveraging mature model quantization technology can decisively resolve cross-platform inconsistencies in learned image compression systems. By prioritizing integer-only arithmetic and innovative parameter discretization, the paper paves the way for deterministic, efficient, and hardware-friendly solutions applicable to contemporary architectures, thereby enhancing practical deployment potential. Future endeavors could explore extending this study to emerging architectures involving more complex neural network layers, potentially broadening the scope of determinism in diverse applications.