Covariance Matrix Adaptation Evolution Strategy Assisted by Principal Component Analysis (2105.03687v2)

Abstract: Over the past decades, more and more methods gain a giant development due to the development of technology. Evolutionary Algorithms are widely used as a heuristic method. However, the budget of computation increases exponentially when the dimensions increase. In this paper, we will use the dimensionality reduction method Principal component analysis (PCA) to reduce the dimension during the iteration of Covariance Matrix Adaptation Evolution Strategy (CMA-ES), which is a good Evolutionary Algorithm that is presented as the numeric type and useful for different kinds of problems. We assess the performance of our new methods in terms of convergence rate on multi-modal problems from the Black-Box Optimization Benchmarking (BBOB) problem set and we also use the framework COmparing Continuous Optimizers (COCO) to see how the new method going and compare it to the other algorithms.

• The paper demonstrates that integrating PCA into CMA-ES significantly reduces computational load while preserving optimization accuracy.
• The methodology employs PCA to derive a reduced-dimensional covariance matrix after initial iterations, streamlining the sampling process.
• Experimental results reveal that PCA-assisted CMA-ES, particularly its stochastic variant, accelerates convergence on multi-modal benchmarks.

Covariance Matrix Adaptation Evolution Strategy Assisted by Principal Component Analysis

Introduction

The paper "Covariance Matrix Adaptation Evolution Strategy Assisted by Principal Component Analysis" explores the integration of Principal Component Analysis (PCA) into the Covariance Matrix Adaptation Evolution Strategy (CMA-ES) for enhancing the performance and reducing computational costs associated with evolutionary algorithms in high-dimensional optimization problems. Evolutionary algorithms are heuristic techniques that can efficiently solve multi-objective optimization problems, but they suffer from computational burdens increasing exponentially with dimensionality. The authors propose a novel approach by incorporating PCA into CMA-ES to dynamically reduce the dimensionality during iterations, potentially alleviating computational burdens while maintaining effective optimization capabilities.

Methodology

Evolutionary Algorithms and CMA-ES

Evolutionary algorithms, such as Genetic Algorithms (GAs), utilize mechanisms inspired by biological evolution, including mutation, crossover, and selection, to optimize solutions through iterative improvement. The CMA-ES improves upon traditional algorithms by automatically adjusting the step size based on a covariance matrix, thereby facilitating more accurate and efficient convergence in numerical optimization tasks.

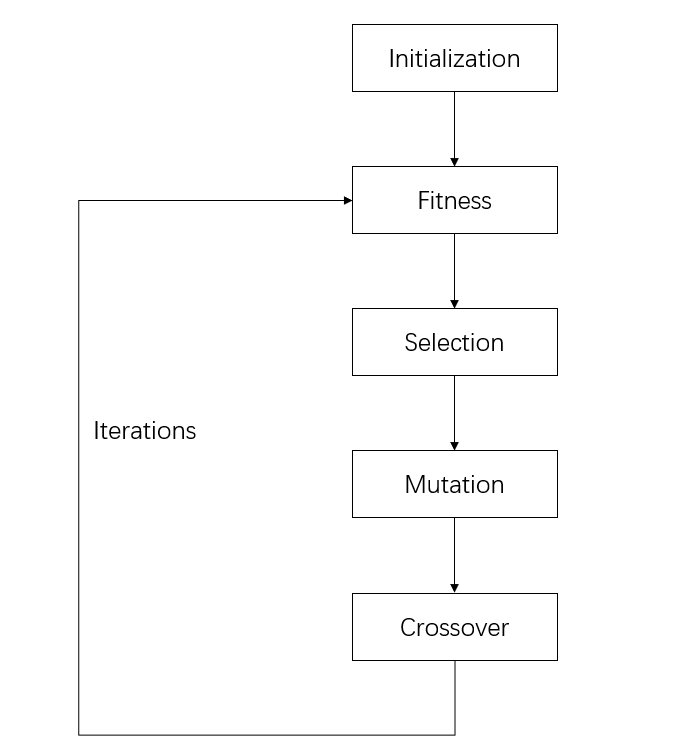
Figure 1: The flow chart of Evolutionary Algorithm.

The covariance matrix adaptation mechanism involves strategically sampling new candidates using Gaussian distributions and leveraging the covariance matrix to control the distribution of solutions. Adjustments to the step size are informed by a comparison between actual evolution paths and paths inferred from random selection, ensuring that step sizes are optimally set to facilitate convergence.

Incorporating PCA

PCA is employed as a dimensionality reduction technique in this framework to streamline the computational process and mitigate noise from extraneous variables. By projecting the high-dimensional data onto a lower-dimensional space defined by principal components, PCA can significantly reduce the computational requirements while preserving the essential characteristics needed for optimization.

In the proposed method, PCA is applied to the sample operation within CMA-ES. Initially, iterations proceed without PCA to establish a baseline from which PCA can derive a transformation matrix. This matrix is subsequently used to compute a new, reduced-dimensional covariance matrix. Sampling within this reduced space allows for efficient generation of potential solutions. The modified solutions are then mapped back to the original dimensional space using an inverse transformation, thereby ensuring the integrity of the optimization process.

Experimental Results

The authors conducted extensive benchmarking of the PCA-assisted CMA-ES on multi-modal functions from the BBOB problem set and compared its performance against standard CMA-ES and a randomly-applied PCA variant, CMA-ES-PCA-Randomly. The experiments spanned multiple dimensions and functions, assessing convergence rates and computational efficiency.

Figure 2: This figure shows the convergence rate of three methods: CMA-ES, CMA-ES-PCA, and CMA-ES-PCA-Randomly. The X-axis indicates the budget while the Y-axis shows the evaluation function value, lower is better.

Comparative Analysis Across Algorithms

The findings reveal distinctive advantages of PCA integration across varying dimensions. While CMA-ES-PCA sometimes struggles with convergence consistency, it can exhibit accelerated convergence in scenarios where initial conditions and problem structure align favorably. Notably, the CMA-ES-PCA-Randomly, which applies PCA stochastically, shows promise in balancing performance stability and computational efficiency.

Figure 3: These four figures show the summary of four algorithms' Empirical cumulative distributions (ECDF) of run lengths and speedup ratios in 2D (top) to 40D (bottom) overall functions.

These results underscore the potential for dimensionality reduction techniques to enhance evolutionary algorithms in complex problem domains without compromising solution fidelity or computational tractability.

Discussion

The integration of PCA as presented in this paper introduces valuable computational efficiencies, particularly evident in scenarios involving higher dimensions where traditional evolutionary strategies falter. While the PCA-assisted approach exhibits occasional convergence instability, its ability to expedite convergence in certain scenarios highlights potential applicability in practical optimization challenges.

The experiments conducted reveal that applying PCA randomly enhances overall stability and performance outcomes, suggesting that adaptive or intelligent application strategies may yield further performance gains. Such strategies balance the benefits of noise reduction and dimensional simplification against the risk of functional deviation caused by dimensional transformations.

Conclusion

In summary, the paper presents a compelling case for integrating PCA into CMA-ES as a means to address the computational challenges inherent to high-dimensional optimization problems. Future work is expected to further refine this integration through intelligent application mechanisms, explore additional dimensionality reduction techniques, and fine-tune PCA parameters to maximize performance stability and solution accuracy.

These insights set the stage for further advancements in evolutionary algorithms, positioning PCA-assisted frameworks as versatile tools capable of tackling complex optimization tasks with enhanced efficiency.