iVPF: Numerical Invertible Volume Preserving Flow for Efficient Lossless Compression

Abstract: It is nontrivial to store rapidly growing big data nowadays, which demands high-performance lossless compression techniques. Likelihood-based generative models have witnessed their success on lossless compression, where flow based models are desirable in allowing exact data likelihood optimisation with bijective mappings. However, common continuous flows are in contradiction with the discreteness of coding schemes, which requires either 1) imposing strict constraints on flow models that degrades the performance or 2) coding numerous bijective mapping errors which reduces the efficiency. In this paper, we investigate volume preserving flows for lossless compression and show that a bijective mapping without error is possible. We propose Numerical Invertible Volume Preserving Flow (iVPF) which is derived from the general volume preserving flows. By introducing novel computation algorithms on flow models, an exact bijective mapping is achieved without any numerical error. We also propose a lossless compression algorithm based on iVPF. Experiments on various datasets show that the algorithm based on iVPF achieves state-of-the-art compression ratio over lightweight compression algorithms.

• The paper presents iVPF, a novel model that achieves efficient lossless compression by establishing precise bijections through volume-preserving flows.
• It utilizes Modular Affine Transformation and discrete invertible 1×1 convolution layers to maintain computational precision and eliminate floating-point errors.
• Experimental results on datasets like CIFAR10 and ImageNet demonstrate that iVPF outperforms previous methods by achieving lower bits-per-dimension values.

Numerical Invertible Volume Preserving Flow for Lossless Compression

Introduction

The paper "iVPF: Numerical Invertible Volume Preserving Flow for Efficient Lossless Compression" (2103.16211) addresses the challenge of efficiently storing large volumes of data, a necessity in today's era due to the exponential growth in data generation. Traditional lossless compression techniques optimize code lengths to approach theoretical limits defined by Shannon's source coding theorem. Recent advancements have leveraged probabilistic models within machine learning frameworks, yielding enhanced compression efficiencies through mechanisms like Normalizing Flows. These models outperform conventional non-machine learning techniques. However, achieving optimal compression within these models is hampered by the inherent continuity of flow models clashing with the discreteness essential for data encoding, necessitating novel computational strategies.

Figure 1: Illustration of IDF(++), LBB, and the proposed iVPF model.

Methodology

The proposed iVPF model builds upon volume-preserving flows, distinguished from non-volume-preserving counterparts by maintaining constant Jacobian determinants, hence enabling more precise bijective mappings necessary for error-free compression. The methodology centers around establishing precise bijections on discretized data domains, thereby enabling exact computational reversibility crucial for lossless compression tasks. This precision is achieved through Modular Affine Transformation (MAT), a novel computational technique described within the paper, designed to eliminate arithmetic errors associated with floating-point operations. Additional layers such as invertible $1 \times 1$ convolution layers are integrated within this architecture, rendered in discrete space, further improving expressivity without detracting from computational efficiency.

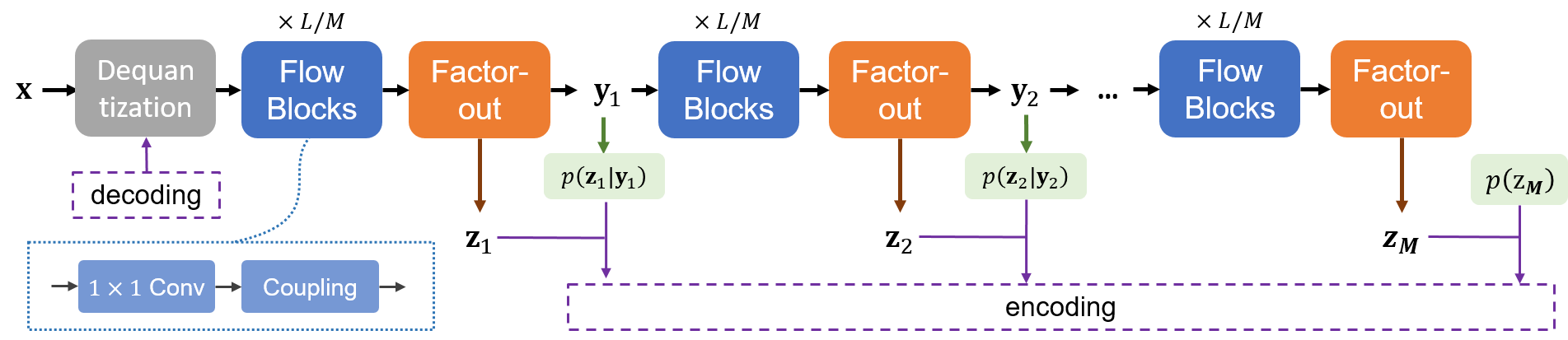
Figure 2: Illustration of the iVPF architecture.

The essence of iVPF lies in constructing a codec model capable of handling discrete data spaces while allowing reversible transformations, crucial for lossless compression. The model leverages discrete quantization and careful layer constructions to ensure no information loss during coding operations, achieving compression ratios surpassing prior benchmarks.

Experimental Results

The empirical evaluation is conducted over several datasets, including CIFAR10 and ImageNet variants, targeted at assessing compression performance metrics such as bits per dimension (bpd) and coding efficiency. The iVPF model demonstrates competitive performance, particularly when benchmarked against existing methods like IDF and IDF++. Errors introduced by the iVPF process are constrained within tolerable limits, ensuring compression ratios closely align with theoretical predictions derived from training over continuous flows.

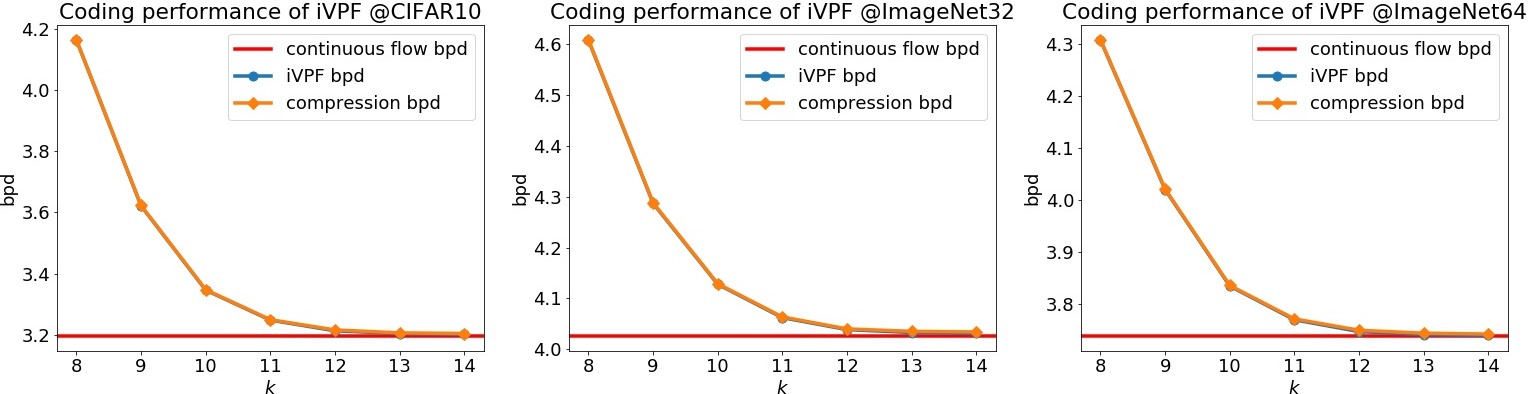
Figure 3: Compression performance of iVPF in terms of bpd.

Comparison with prior state-of-the-art methods highlights iVPF's advantage in achieving lower bpd values across various datasets, irrespective of image scale. Furthermore, real-world high-resolution image datasets further evidence iVPF's robustness over conventional codecs like PNG and FLIF, validating the model's applicability across diverse data types and resolution scales.

Implications and Future Prospects

The development of iVPF marks a significant step in aligning computational model precision with the practical requirements of lossless data compression. By bridging discrete data handling within continuous probabilistic frameworks, the technique sets a precedent for future research, potentially extending beyond image data into varied domains such as audio and video data compression. The implications of such advancements lie in fostering improved storage efficiencies, critical within data-intensive fields, and encouraging further exploration within machine learning-driven compression strategies.

Conclusions

The paper successfully delivers a robust and efficient model capable of addressing the shortcomings of existing flow-based methods within data compression regimes. By securing exact bijective mappings and enhancing layer expressivity, iVPF stands poised to influence future developments in data compression research, paving the way for increasingly efficient generative models to tackle evolving data challenges.