3D Probabilistic Segmentation and Volumetry from 2D projection images

Abstract: X-Ray imaging is quick, cheap and useful for front-line care assessment and intra-operative real-time imaging (e.g., C-Arm Fluoroscopy). However, it suffers from projective information loss and lacks vital volumetric information on which many essential diagnostic biomarkers are based on. In this paper we explore probabilistic methods to reconstruct 3D volumetric images from 2D imaging modalities and measure the models' performance and confidence. We show our models' performance on large connected structures and we test for limitations regarding fine structures and image domain sensitivity. We utilize fast end-to-end training of a 2D-3D convolutional networks, evaluate our method on 117 CT scans segmenting 3D structures from digitally reconstructed radiographs (DRRs) with a Dice score of $0.91 \pm 0.0013$. Source code will be made available by the time of the conference.

• The paper introduces two probabilistic deep learning models, 2D to 3D MC-Dropout-U-Net and PhiSeg, to transform 2D X-ray images into 3D volumetric segmentations.
• The proposed methods achieve high accuracy with a Dice coefficient of 0.90 for large anatomical structures and demonstrate robustness across different datasets.
• This approach addresses the inherent loss of volumetric data in X-ray imaging, potentially enhancing diagnostic workflows by reducing radiation exposure compared to CT scans.

3D Probabilistic Segmentation and Volumetry from 2D Projection Images

Introduction

This paper presents a probabilistic approach to reconstructing 3D volumetric images from 2D projection images, specifically focusing on X-ray imaging. While X-rays are advantageous for their speed, cost-effectiveness, and reduced radiation exposure compared to CT scans, they inherently suffer from the loss of volumetric information due to their projective nature. This research explores methods to utilize deep learning architectures adapted for 2D to 3D transformation to overcome this limitation and assess the performance and confidence of reconstructed 3D images.

Methodology

The core methodology involves adapting known 2D or 3D architectures to facilitate 2D to 3D transformation. The authors propose two main approaches: a 2D to 3D MC-Dropout-U-Net and a 2D to 3D PhiSeg.

2D to 3D MC-Dropout-U-Net

The MC-Dropout-U-Net extends the U-Net architecture to three dimensions, incorporating dropout layers in the decoding path to maintain stochastic behavior during inference (Figure 1). This approach begins with a structural reconstruction module that transforms 2D inputs into a 3D structure, followed by segmentation using a 3D U-Net. Dropout is applied to the decoding layers during inference to model uncertainty in the predictions.

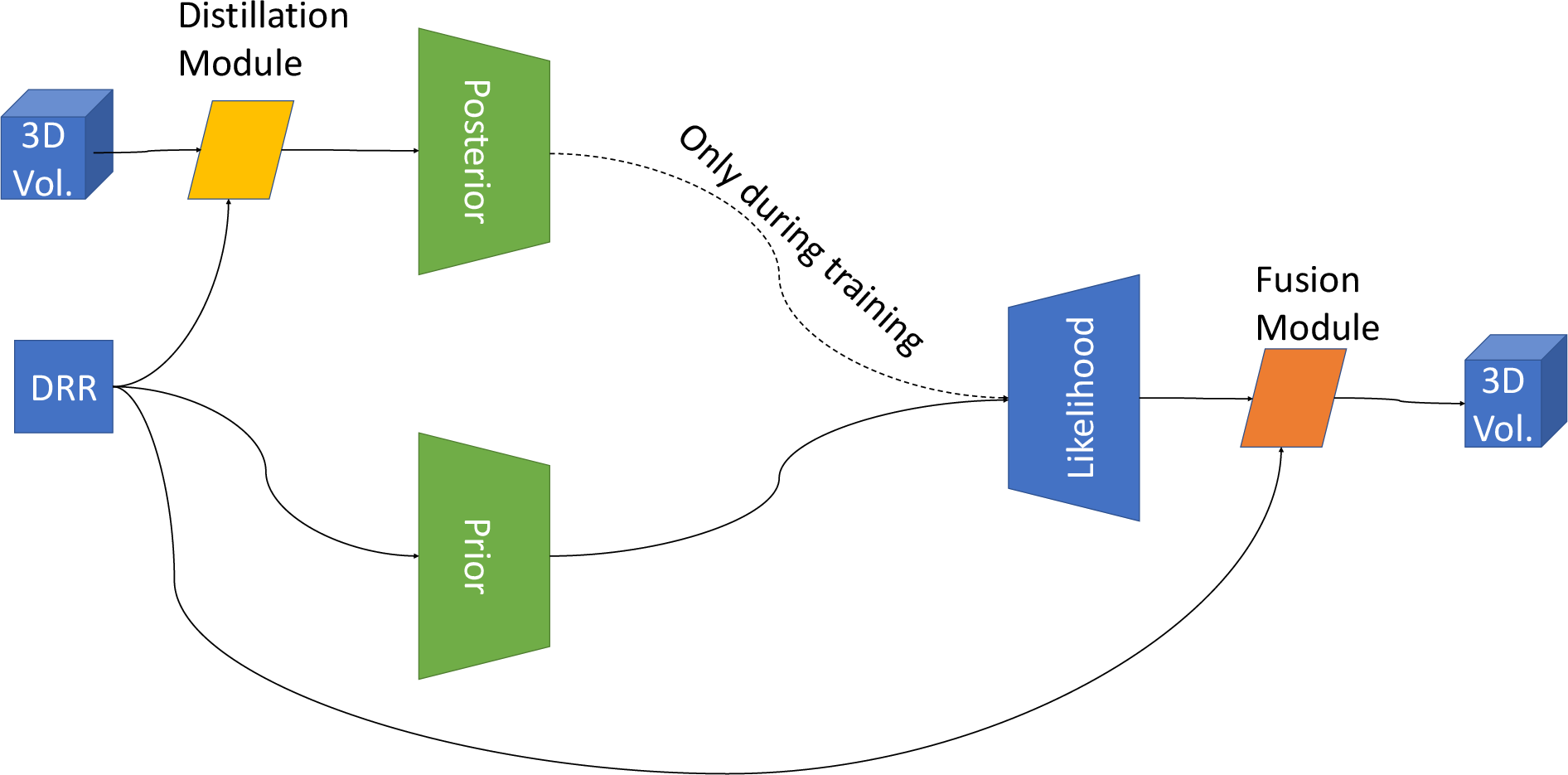
Figure 1: Two approaches for probabilistic 2D-3D un-projection.

2D to 3D PhiSeg

The PhiSeg model builds upon a Conditional Variational Auto-Encoder framework to achieve probabilistic segmentation. It involves a distillation module for compressing 3D information into a 2D representation, followed by encoding and decoding through learned latent variables sampled from a probabilistic distribution. This method aims to enhance fine structural segmentation by integrating a fusion module, combining high-level details from the DRR input with the decoded segmentation.

Experiments and Results

The experiments conducted focus on two primary tasks: segmentation and volumetry across multiple datasets, testing the limitations of the proposed methods on fine, unconnected structures.

Compact Structures (Experiment 1)

Utilizing a thoracic CT dataset, the models were tasked with segmenting large, connected regions such as the lungs. The experiments achieved an average Dice similarity coefficient (DSC) of 0.90 for the 2D-3D U-Net with dropout, demonstrating its effectiveness in segmenting large anatomical structures.

Fine Structures (Experiment 2)

The second experiment focused on the segmentation of fine structures using a porcine ribcage dataset. Here, the 2D-3D U-Net with dropout achieved a Dice score of 0.48, indicating the capacity to capture fine structures but also highlighting challenges with disconnected anatomy.

Figure 2: Reconstructed Samples for Experiments 1,2. We use~\cite{kroes2012exposure} to enhance depth perception in the 3D figures.

Domain Adaptation (Experiment 3)

Experiment 3 evaluated the models' domain adaptability using NIH chest X-ray data. Results demonstrated that the models could generalize well to new datasets, suggesting robustness in varying imaging domains.

Figure 3: Examples from Experiment 3.

Discussion

The study underscores the utility of probabilistic methods in reconstructing 3D volumes from 2D projections, addressing projective information loss by employing learning-based extrapolation approaches. These methods show potential for application in clinical workflows where rapid 3D reconstruction from 2D X-rays can expedite diagnosis while mitigating patient exposure to higher radiation doses associated with CT scans.

Despite the promising results, the challenge remains in accurately predicting disconnected fine structures and adapting to unseen data domains. Future improvements could focus on refining probabilistic representations to enhance detail reconstruction and extending these methods for unsupervised domain adaptation tasks.

Conclusion

The paper introduces a novel approach to obtaining 3D volumetric information from 2D X-ray images through probabilistic segmentation techniques. The proposed network architectures, particularly the incorporation of dropout for uncertainty estimation and probabilistic encoding-decoding pathways, have demonstrated potential in achieving accurate reconstructions with confidence intervals. Future work may explore this methodology's application to more complex anatomical structures and different imaging modalities, promising significant advancements in diagnostic radiology.