A Primer on Reproducing Kernel Hilbert Spaces

Abstract: Reproducing kernel Hilbert spaces are elucidated without assuming prior familiarity with Hilbert spaces. Compared with extant pedagogic material, greater care is placed on motivating the definition of reproducing kernel Hilbert spaces and explaining when and why these spaces are efficacious. The novel viewpoint is that reproducing kernel Hilbert space theory studies extrinsic geometry, associating with each geometric configuration a canonical overdetermined coordinate system. This coordinate system varies continuously with changing geometric configurations, making it well-suited for studying problems whose solutions also vary continuously with changing geometry. This primer can also serve as an introduction to infinite-dimensional linear algebra because reproducing kernel Hilbert spaces have more properties in common with Euclidean spaces than do more general Hilbert spaces.

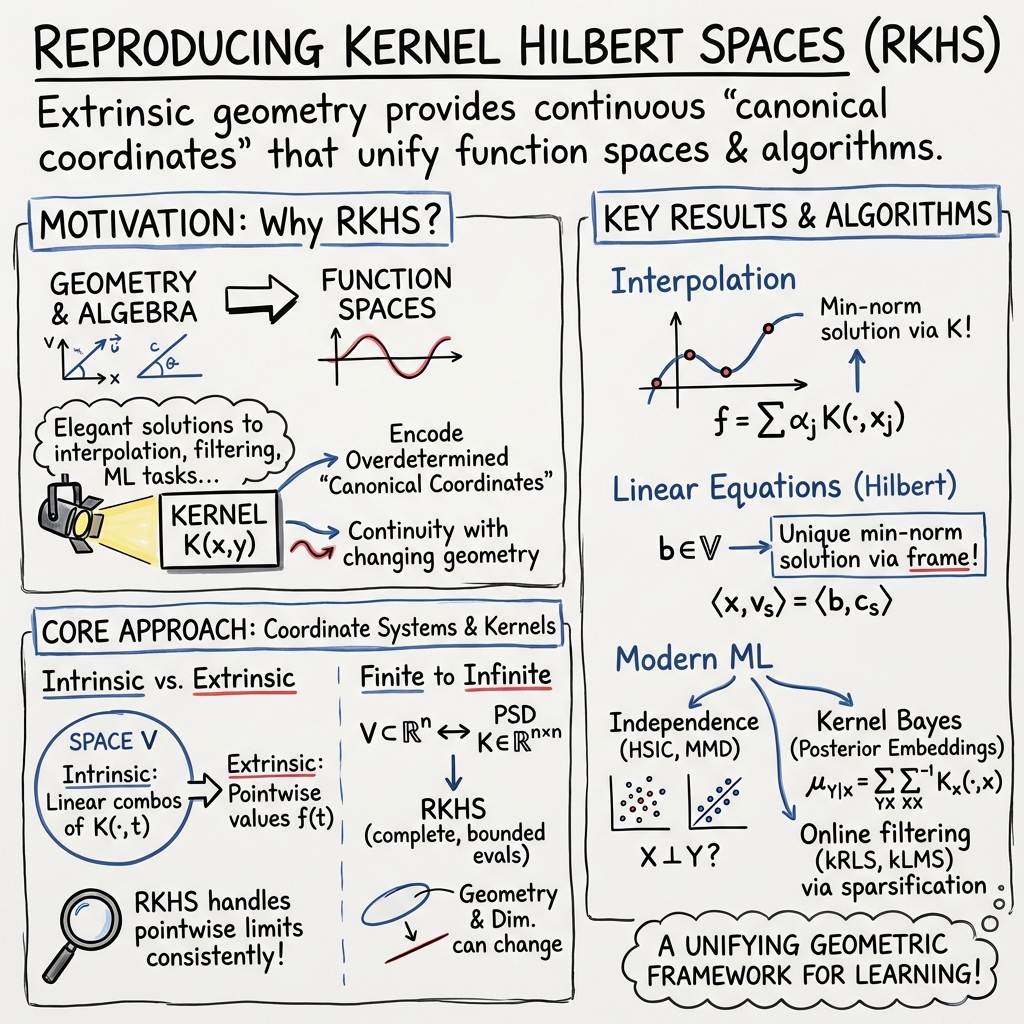
• The paper introduces RKHS theory as a transformative framework linking geometric reasoning with positive semi-definite kernels for efficient problem solving.
• The primer illustrates RKHS applications in signal processing, support vector machines, and statistical inference through concrete visual examples.
• The work simplifies complex continuous geometry problems by embedding finite-dimensional subspaces into manageable RKHS models.

A Primer on Reproducing Kernel Hilbert Spaces

Introduction

Reproducing Kernel Hilbert Spaces (RKHSs) are pivotal in theoretical and applied mathematics, particularly in fields requiring a synergy between geometric reasoning and symbolic manipulation. The primer by Manton and Amblard provides an insightful introduction to RKHS without presupposing prior knowledge of Hilbert spaces, emphasizing their utility in signal processing and systems theory applications. This contribution explores RKHS by associating geometric configurations with canonical overdetermined coordinate systems, highlighting their efficacy in handling continuous geometry-related problems.

RKHS Definition and Motivation

RKHS theory is conventionally seen as a transform theory between RKHSs and positive semi-definite functions, or kernels, such that each RKHS uniquely corresponds to a kernel. Importantly, RKHS theory captures not only intrinsic properties but also extrinsic geometries, illustrating why problem-solving is more efficient via kernels rather than direct spatial solutions. The primer progresses RKHS theory in finite dimensions, allowing the manipulation of Euclidean-like spaces sans complexities of infinite dimensions, thus facilitating a comprehensive understanding of their characteristics.

Key Applications

RKHS boasts several potent applications:

1. Subspace Problems: RKHSs aid in resolving problems where embedding a subspace into a function space is advantageous, especially in cases involving difficult limit sequence calculations.
2. Positive Semi-definite Functions: Problems like those involving stochastic processes can be aligned with RKHS via their kernels. The covariance function of such processes serves as a kernel, enabling robust problem-solving strategies.
3. Support Vector Machines: AI models utilize RKHS theory to manage non-linear issues by transforming them into linear ones through specified embeddings, underscoring RKHS’s profound impact on machine learning methodologies.

RKHS integration into signal processing and statistical inference offers a unified framework, often rendering more elegant and insightful solutions compared to traditional techniques. The primer not only highlights practical examples but also discusses the profound theoretical underpinnings of RKHS landscapes.

Visual Representations and Examples

The primer showcases RKHS functionality through visual examples, notably embedding subspaces with intrinsic and extrinsic coordinates. This visual methodology demystifies complex spatial configurations into comprehensible geometries, fostering intuitive insights into RKHS operations. Furthermore, tailored examples like finite-dimensional RKHS spaces elucidate how abstract linear algebra principles translate to RKHS mechanics.

Conclusion

The work of Manton and Amblard in this primer serves as an invaluable introduction, offering clarity and depth in understanding RKHS theory’s implications. With its detailed explanations and practical insights, it empowers researchers to leverage RKHS in various domains, facilitating precise mathematical and statistical modeling. As AI and computational methods advance, the role of RKHS in unifying complex dynamic systems into coherent, solvable models becomes increasingly pivotal, paving the way for innovation in both academic and practical landscapes.