Krylov complexity and Wightman power spectrum with positive chemical potentials in Schrödinger field theory (2509.14742v2)

Abstract: We systematically investigate the Krylov complexity of fermionic fields in Schr\"odinger field theory as the chemical potential is positive, validated by the engineered Wightman power spectra. For non-positive chemical potentials, the Lanczos coefficients exhibit linear behaviors with respect to $n$. However, as the chemical potential becomes positive, a dynamical transition occurs -- Lanczos coefficient $b_{n}$ develops a two-stage linear growth profile, transitioning from an initial slope of $\pi/\beta$ to the asymptotic slope of $2/\beta$; while Lanczos coefficient $a_{n}$ shows a deflection from near-zero values to linear descent with slope $-4/\beta$ where $\beta$ is the inverse temperature. Moreover, the engineered power spectra are used to study the evolution of the Krylov complexity and some universal behaviors are uncovered -- the single-sided exponential decay of the power spectrum results in the quadratic growth of the complexity, consistent with that from the $SL(2,\mathbb{R})$ algebraic construction. Conversely, the double-sided exponential decay of the power spectrum restores the exponential growth of the complexity, satisfying the maximal chaos bound. These results may provide new insights into the profound impact of chemical potential on the operator growth and Krylov complexity in the quantum field theory.

• The paper demonstrates a two-stage evolution of Lanczos coefficients, linking positive chemical potentials to a dynamical transition in operator growth.
• It employs the Lanczos algorithm to map operator spread to a discrete Schrödinger equation, confirming quadratic complexity growth in specific regimes.
• The study establishes how the decay properties of the Wightman power spectrum influence complexity progression and quantum chaos bounds.

Krylov Complexity and Wightman Power Spectrum in Schrödinger Field Theory with Positive Chemical Potentials

This paper presents a systematic analysis of Krylov complexity for fermionic fields in Schrödinger field theory under positive chemical potentials, with a focus on the interplay between operator growth, Lanczos coefficients, and the structure of the Wightman power spectrum. The paper elucidates the dynamical transition in operator complexity as the chemical potential is tuned, and establishes connections to $SL(2,\mathbb{R})$ algebraic structures and chaos bounds.

Mathematical Framework and Operator Growth

Krylov complexity quantifies the spread of an operator in the Krylov basis generated by the Liouvillian superoperator $\mathcal{L} = [H, \cdot]$. The Lanczos algorithm constructs an orthonormal basis $\{\mathcal{O}_n\}$, with recursion relations parameterized by Lanczos coefficients $a_n$ and $b_n$. The time evolution of the operator is mapped to a discrete Schrödinger equation for the coefficients $\varphi_n(t)$, and the Krylov complexity is defined as $K(t) = 1 + \sum_n n |\varphi_n(t)|^2$.

The moments $\mu_n$ of the Wightman power spectrum $f^W(\omega)$, given by $$\mu_n = \frac{1}{2\pi} \int f^W(\omega) \omega^n d\omega$$, are central to the computation of the Lanczos coefficients via nonlinear recurrence relations. The structure of $f^W(\omega)$, particularly its support and decay properties, directly influences the asymptotic behavior of the Lanczos coefficients and, consequently, the growth of Krylov complexity.

Lanczos Coefficients and Chemical Potential Dependence

For non-positive chemical potentials, the Lanczos coefficients in Schrödinger field theory exhibit simple linear scaling: $\beta a_n \approx -4(n+1) + \mu$ and $\beta b_n \approx 2n+1$, leading to exponential growth of Krylov complexity at a rate $\lambda_K \ll 2\pi/\beta$. This behavior is largely insensitive to the sign and magnitude of the chemical potential in the negative regime.

In contrast, for positive chemical potentials, the paper reveals a distinct two-stage linear growth in $b_n$ and a deflection in $a_n$:

• $a_n$ remains near zero for small $n$, then transitions to a linear descent with slope $-4/\beta$ at a deflection point that shifts to larger $n$ as $\mu$ increases.
• $b_n$ initially grows linearly with slope $\pi/\beta$, then transitions to a slope of $2/\beta$ at the same deflection point.

(Figure 1)

Figure 1: Lanczos coefficients $a_n$ and $b_n$ for various positive chemical potentials, showing the two-stage linear growth and deflection behavior.

The location of the deflection in both $a_n$ and $b_n$ increases with $\mu$, indicating a dynamical transition in operator growth as the system moves deeper into the high-density regime.

Asymptotic Growth of Krylov Complexity

The late-time behavior of Krylov complexity is determined by the asymptotic scaling of the Lanczos coefficients. By mapping the large-$n$ behavior to the $SL(2,\mathbb{R})$ algebraic construction, where $a_n \sim \gamma n$ and $b_n \sim \alpha n$, the paper identifies the regime $\gamma^2 = 4\alpha^2$ as corresponding to quadratic growth of complexity: $K(t) \sim t^2$.

This is in stark contrast to the exponential growth observed for non-positive chemical potentials and for power spectra with double-sided exponential decay. The quadratic growth is analytically confirmed by both direct solution of the discrete Schrödinger equation and by comparison to the $SL(2,\mathbb{R})$ spread complexity formula.

(Figure 2)

Figure 2: Time evolution of Krylov complexity for various positive chemical potentials, demonstrating the crossover from exponential to quadratic growth as $\mu$ increases.

Wightman Power Spectrum Engineering and Complexity Growth

The paper explores the impact of the Wightman power spectrum's support and decay properties on operator complexity:

• Single-sided exponential decay (e.g., $f^W(\omega) \propto e^{\kappa \omega}$ for $\omega \leq 0$) leads to quadratic growth of Krylov complexity.
• Double-sided exponential decay (e.g., $f^W(\omega) \propto e^{-\beta |\omega|/2}$) restores exponential growth, saturating the maximal chaos bound.

(Figure 3)

Figure 3: Comparison of Krylov complexity for single-sided and double-sided exponentially decaying Wightman power spectra, illustrating the transition from quadratic to exponential growth.

The paper further demonstrates that the presence and nature of frequency cutoffs in $f^W(\omega)$ (single-sided, symmetric, or asymmetric) manifest as deflections or plateaus in the Lanczos coefficients. Single-sided cutoffs induce a single deflection, symmetric cutoffs produce a plateau, and asymmetric double-sided cutoffs result in two deflections followed by a plateau.

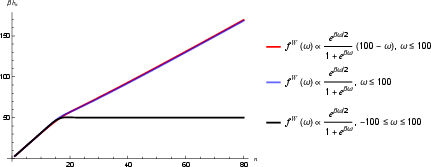
Figure 4: Lanczos coefficients $a_n$ and $b_n$ for different truncations of the Wightman power spectrum, showing the correspondence between spectral cutoffs and coefficient inflections.

Implications and Future Directions

The results establish a clear link between the spectral properties of the Wightman function and the dynamical complexity of operator growth in quantum field theory. The identification of a quadratic growth regime for positive chemical potentials, and its connection to $SL(2,\mathbb{R})$ algebraic structures, provides a new perspective on the universality of operator growth and its sensitivity to thermodynamic parameters.

The findings have implications for the paper of quantum chaos, thermalization, and information propagation in many-body systems, particularly in regimes of high fermion density. The sensitivity of Krylov complexity to the detailed structure of the power spectrum suggests that engineered spectral features could be used to control operator growth and complexity in quantum simulators.

Future work may address the role of non-Hermitian operators, the impact of more general spectral truncations, and the extension to interacting or higher-dimensional field theories. The connection to holographic duality and the interpretation of complexity growth in terms of bulk geometric quantities also remains a promising direction.

Conclusion

This paper provides a comprehensive analysis of Krylov complexity in Schrödinger field theory with positive chemical potentials, revealing a dynamical transition in operator growth characterized by a crossover from exponential to quadratic complexity growth. The work highlights the critical role of the Wightman power spectrum's structure in determining operator dynamics and establishes a framework for understanding complexity in terms of algebraic and spectral data. These insights contribute to the broader understanding of quantum chaos, operator spreading, and the interplay between thermodynamics and complexity in quantum field theory.