Discovery of Unstable Singularities (2509.14185v1)
Abstract: Whether singularities can form in fluids remains a foundational unanswered question in mathematics. This phenomenon occurs when solutions to governing equations, such as the 3D Euler equations, develop infinite gradients from smooth initial conditions. Historically, numerical approaches have primarily identified stable singularities. However, these are not expected to exist for key open problems, such as the boundary-free Euler and Navier-Stokes cases, where unstable singularities are hypothesized to play a crucial role. Here, we present the first systematic discovery of new families of unstable singularities. A stable singularity is a robust outcome, forming even if the initial state is slightly perturbed. In contrast, unstable singularities are exceptionally elusive; they require initial conditions tuned with infinite precision, being in a state of instability whereby infinitesimal perturbations immediately divert the solution from its blow-up trajectory. In particular, we present multiple new, unstable self-similar solutions for the incompressible porous media equation and the 3D Euler equation with boundary, revealing a simple empirical asymptotic formula relating the blow-up rate to the order of instability. Our approach combines curated machine learning architectures and training schemes with a high-precision Gauss-Newton optimizer, achieving accuracies that significantly surpass previous work across all discovered solutions. For specific solutions, we reach near double-float machine precision, attaining a level of accuracy constrained only by the round-off errors of the GPU hardware. This level of precision meets the requirements for rigorous mathematical validation via computer-assisted proofs. This work provides a new playbook for exploring the complex landscape of nonlinear partial differential equations (PDEs) and tackling long-standing challenges in mathematical physics.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Explain it Like I'm 14
Overview
This paper is about a big mystery in math and physics: can the equations that describe how fluids move suddenly “blow up,” meaning certain values (like how fast the fluid is spinning) become infinite in a finite amount of time? The authors use a mix of clever math and machine learning to discover new examples of these “blow-ups,” especially the hard-to-find kind called unstable singularities. They also reach very high accuracy, good enough to help future rigorous math proofs.
Key questions the paper asks
- Can we find unstable singularities (the most delicate, easily disturbed blow-ups) in important fluid equations?
- Can we do this reliably and with such high precision that mathematicians could later turn these discoveries into proofs?
- Is there a simple pattern that connects how “unstable” a singularity is to how fast it blows up?
How they approached the problem (in everyday language)
What is a “singularity” here?
Imagine stirring a fluid. Most of the time, things stay smooth. A singularity is like a sudden, extreme event where some quantity (for example, the steepness of a wave or how quickly the fluid spins) skyrockets to infinity in a finite time. It’s like a whirlpool that gets sharper and sharper until it becomes infinitely sharp.
Stable vs. unstable singularities
- Stable singularity: Like a ball at the bottom of a bowl. If you nudge it a bit, it rolls back and still falls into the same spot. These are easier to find with simulations.
- Unstable singularity: Like trying to balance a pencil on its tip. The tiniest breath of air will make it fall. These are very hard to find and keep track of in computations because even tiny errors push you off course.
The paper focuses on finding the unstable kind, which many believe are the ones that matter most for the hardest open problems (like the famous Navier–Stokes Millennium Prize Problem).
Self-similar coordinates: zooming in smartly
Near a singularity, things change very fast. To handle that, the authors use “self-similar coordinates.” Think of zooming in on a tornado so that, as time goes on, the picture keeps the same shape while you rescale space and time. In these coordinates, instead of simulating a wild movie, you “freeze” the picture and look for a smooth, steady shape (the “profile”) and a number that controls how fast it blows up (called the scaling rate, written as ).
- The job becomes: find the smooth profile and the right that make the transformed equations hold everywhere.
How they used machine learning (PINNs) plus a precise optimizer
- PINNs (Physics-Informed Neural Networks) are neural networks that are trained to satisfy the equation itself (not just data). You feed the network the coordinates; it outputs the solution; and the training loss tells you how badly it disobeys the physics.
- They build the network with math “hints”:
- Impose symmetries and boundary behavior.
- Transform infinite domains into manageable ones.
- Use “solution envelopes” to bake in how the solution behaves near the center and far away.
- Use math relationships to guide or even determine instead of guessing it.
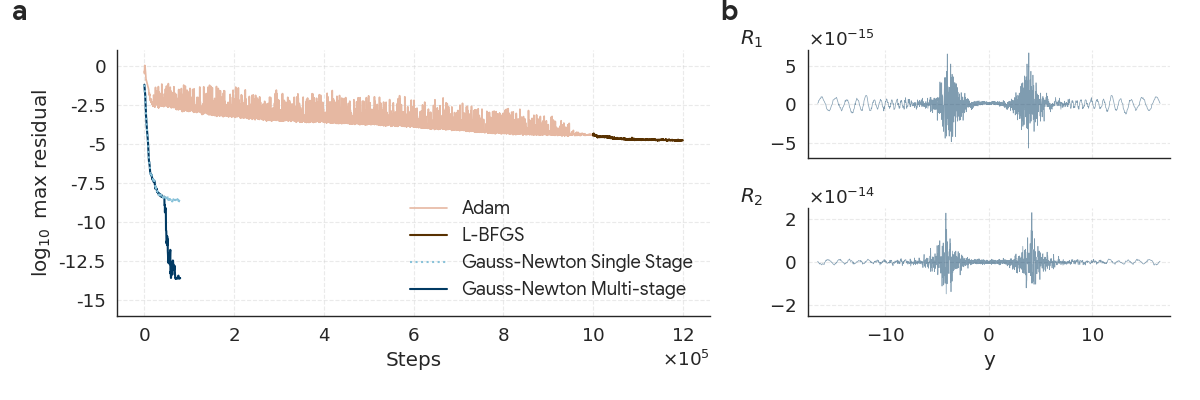
- High-precision training:
- They use a Gauss–Newton optimizer (a powerful, second-order method) instead of standard optimizers like Adam or L-BFGS. This helps reach much higher accuracy.
- They also use “multi-stage training”: train one network to get close, then train a second to fix the leftover errors (especially high-frequency wiggles).
Checking that the solutions are real and accurate
- Residual check: Plug the network’s solution back into the equations everywhere and measure the largest error (the “maximum residual”). Smaller is better.
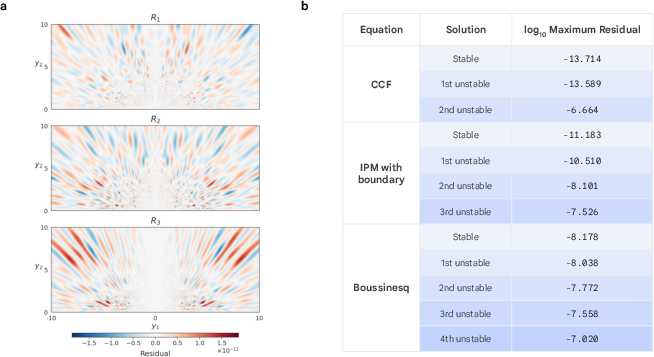
- Stability check: Linearize the equations around the found profile and count how many directions are unstable. For the “-th unstable” solution, you should see unstable directions. This is exactly what they find.
- Precision: For some solutions (in a simpler 1D model known as CCF), they get errors as small as about , which is near the limit of standard computer number precision.
Main findings and why they matter
- They discovered several new unstable self-similar singularities in:
- The CCF model (a simplified equation related to fluid motion),
- The 2D incompressible porous media (IPM) equation,
- The 2D Boussinesq equations (with a boundary), which are closely related to the 3D Euler equations with axial symmetry and a boundary.
- They achieved very high accuracy:
- Typical errors around to for IPM and Boussinesq,
- Near machine precision (about ) for certain CCF solutions.
- This level of accuracy is a key requirement for rigorous computer-assisted proofs.
- They found a simple pattern linking instability level and blow-up speed:
- Each unstable solution has a scaling rate . Smaller means more unstable and faster blow-up.
- For Boussinesq/Euler-with-boundary and IPM, they observed an almost linear rule for how changes as the number of unstable directions grows. In short, as increases, follows a simple trend you can predict.
- They improved what we know about when dissipation still allows blow-up in the CCF model:
- They found higher-order unstable solutions and refined earlier ones, pushing the boundary (a parameter often called ) up to about $0.68$ for which blow-up is expected. This sharpens our understanding of when “smoothing effects” can and cannot stop singularities.
Why this is important:
- Unstable singularities are believed to be the kind relevant to the hardest open problems, like whether the famous Navier–Stokes equations can blow up.
- Having a reliable way to discover and verify such solutions is a significant step forward, and their extreme accuracy opens the door to formal mathematical proofs.
What this could lead to
- A new “playbook” for exploring very complex fluid equations:
- Combine math insights (symmetry, scaling, boundary behavior) with specialized machine learning and high-precision optimization.
- Better guidance for future searches:
- The simple patterns in give good starting guesses for finding even higher-order unstable solutions.
- Progress toward big open problems:
- Although the toughest case (like the 3D Euler/Navier–Stokes without boundaries) remains unsolved, this work develops the tools and strategies likely needed to tackle it.
- Stronger bridges between computation and proof:
- Solutions accurate enough for computer-assisted proofs can help turn numerical discoveries into theorems, advancing both mathematics and physics.
In short, the authors show how to reliably find the most delicate kinds of fluid “blow-ups,” do it with record-setting precision, and uncover simple rules behind them—all of which could help unlock long-standing mysteries about how fluids behave at their most extreme.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise, actionable list of what remains missing, uncertain, or unexplored in the paper.
- Boundary-free Euler/Navier–Stokes singularities: No unstable self-similar solutions were discovered for boundary-free 3D Euler or Navier–Stokes; existence, structure, and admissible sequence in the boundary-free setting remain open.
- Rigorous validation (CAP) beyond CCF: Computer-assisted proofs are only indicated as “in preparation” for CCF; rigorous interval-arithmetic validation, enclosure of , and certified residual bounds for IPM and Boussinesq profiles are not yet provided.
- Fourth unstable Boussinesq profile unresolved: The candidate 4th unstable solution is not validated (no reliable or residual certification); a precise workflow to achieve CAP-level accuracy is missing.
- Completeness and uniqueness at fixed instability order: It is not established whether the -th order unstable singularity is unique (up to symmetries) or whether multiple discrete solutions (or continua) exist for the same instability order.
- Symmetry restrictions in discovery and stability: All solutions and linear stability analyses are performed under specific symmetry/parity and boundary conditions; symmetry-breaking modes, non-axisymmetric perturbations, and alternative boundary geometries are not analyzed.
- Linear vs nonlinear stability: Only linear spectra are computed; nonlinear (in)stability, mode coupling, and behavior along center/unstable manifolds are unquantified.
- Dynamical realization and manifolds: There is no time-dependent verification that trajectories in rescaled variables approach/repel the computed profiles; the dimension/codimension and structure of stable/unstable manifolds, and explicit construction of initial data that land on these trajectories, are not characterized.
- Empirical –instability law lacks theory: The observed linear law of inverse scaling rate vs instability order for IPM and Boussinesq is empirical; its theoretical derivation, range of validity, asymptotics as , and error quantification are open.
- No asymptotic law for CCF: Higher-order unstable CCF profiles are not available at sufficient accuracy to infer an asymptotic relationship; it remains unclear whether a similar linear trend holds.
- Fractional dissipation thresholds in CCF: Only up to the second unstable profile is used to update the critical threshold (to ); whether higher-order profiles further raise this threshold or yield the optimal bound is unknown.
- Viscous persistence: The conjecture that higher-instability Euler/Boussinesq/IPM profiles persist under viscosity (Navier–Stokes or fractional dissipation) is untested; quantitative regimes, scaling laws, and perturbative matching are not established.
- Effects of exponentially small boundary terms: For the Boussinesq/Euler analogy “up to exponentially small terms,” the impact of these corrections on high-order unstable solutions, their spectra, and is not quantified.
- Residual metric adequacy: Accuracy is reported via maximum PDE residual on a dense grid; rigorous a posteriori error estimators in continuous norms, aliasing analysis, and guarantees against grid-induced bias are missing.
- identification and uncertainty: The selection via smoothness constraints and perturbation tests lacks rigorous uniqueness and error bars; sensitivity to the choice of solution envelope and coordinate transforms is not quantified.
- Sensitivity to architecture and training choices: The dependence of discovered solutions on PINN architecture, activation functions, solution envelopes, compactification maps, sampling strategy, and multistage training is not systematically studied.
- Scalability of optimization: The full-matrix Gauss–Newton approach depends on small networks; how to scale to higher-dimensional, less symmetric problems (e.g., full 3D Euler without boundaries) while maintaining precision remains open.
- Precision and reproducibility: Results rely on GPU double precision and report being round-off limited; reproducibility across hardware, potential benefits of arbitrary-precision arithmetic, and formal uncertainty quantification for eigenvalues//residuals are not addressed.
- Infinite-domain modeling choices: The compactification and envelope factors may bias the solution space; comparisons with alternative bases (e.g., rational spectral, conformal maps) and their effect on accuracy and discoverability are not explored.
- Time-integration verification: Stabilized time-stepping or shadowing methods to confirm self-similar attractor/repellor behavior in full PDE dynamics near the candidate profiles are not presented.
- Higher-order solutions beyond those reported: Systematic procedures and initializations to robustly discover higher-order unstable Boussinesq/IPM/CCF solutions (beyond those obtained here) are not established.
- Physical interpretability and detection: How instability order and map to observable signatures in direct numerical simulations or experiments, and how to target or detect specific unstable profiles in practice, are not specified.
- Extension to other PDEs: The approach is not tested on related equations with known or suspected unstable blow-up (e.g., SQG, vortex sheets, water waves, non-axisymmetric 3D Euler); transferability and required adaptations are unknown.
- Data/code availability for community CAP: Public release of profiles, values, training configurations, and validation grids to facilitate independent CAPs and benchmarking is not specified.
Collections
Sign up for free to add this paper to one or more collections.