Geometric Neural Distance Fields for Learning Human Motion Priors (2509.09667v1)

Abstract: We introduce Neural Riemannian Motion Fields (NRMF), a novel 3D generative human motion prior that enables robust, temporally consistent, and physically plausible 3D motion recovery. Unlike existing VAE or diffusion-based methods, our higher-order motion prior explicitly models the human motion in the zero level set of a collection of neural distance fields (NDFs) corresponding to pose, transition (velocity), and acceleration dynamics. Our framework is rigorous in the sense that our NDFs are constructed on the product space of joint rotations, their angular velocities, and angular accelerations, respecting the geometry of the underlying articulations. We further introduce: (i) a novel adaptive-step hybrid algorithm for projecting onto the set of plausible motions, and (ii) a novel geometric integrator to "roll out" realistic motion trajectories during test-time-optimization and generation. Our experiments show significant and consistent gains: trained on the AMASS dataset, NRMF remarkably generalizes across multiple input modalities and to diverse tasks ranging from denoising to motion in-betweening and fitting to partial 2D / 3D observations.

• The paper introduces Neural Riemannian Motion Fields (NRMF) as a generative framework that models plausible 3D human motion using neural distance fields.
• The method leverages Riemannian geometry to enforce physically consistent joint rotations, velocities, and accelerations, improving motion recovery.
• Extensive experiments demonstrate that NRMF outperforms state-of-the-art baselines in accuracy, temporal consistency, and motion diversity.

Geometric Neural Distance Fields for Learning Human Motion Priors

Introduction and Motivation

The paper introduces Neural Riemannian Motion Fields (NRMF), a generative framework for modeling 3D human motion priors that explicitly respects the geometry of articulated bodies. Unlike prior approaches based on VAEs or diffusion models, NRMF leverages neural distance fields (NDFs) defined on the product space of joint rotations, angular velocities, and angular accelerations. This construction enables the modeling of plausible poses, transitions, and accelerations as zero-level sets of learned neural fields, providing a rigorous and expressive prior for human motion. The framework is designed to address limitations in temporal consistency, physical plausibility, and generalization across diverse input modalities, which are persistent challenges in human motion recovery from sparse or noisy data.

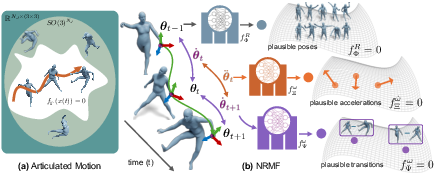
Figure 1: NRMF models the space of plausible poses, transitions, and accelerations as zero-level sets of neural distance fields, enabling robust motion recovery and generation.

Mathematical Formulation and Geometric Foundations

NRMF is grounded in the Riemannian geometry of articulated motion. The state of a human body is represented as a tuple comprising root translation, joint rotations ($SO(3)^{N_J}$), angular velocities, and angular accelerations. The motion manifold is defined as the zero-level set of an implicit function $f_\Gamma$ over the product space $$M = SO(3)^{N_J} \times so(3)^{N_J} \times \mathbb{R}^{3 \times N_J}$$, where each component corresponds to pose, transition, and acceleration plausibility, respectively.

The projection of arbitrary motion states onto the manifold of plausible motions is performed via a three-stage adaptive-step gradient descent, utilizing Riemannian gradients and exponential maps to ensure updates remain on the manifold. The geometric integrator enables the rollout of motion sequences by integrating plausible accelerations and velocities, correcting for drift and enforcing physical consistency.

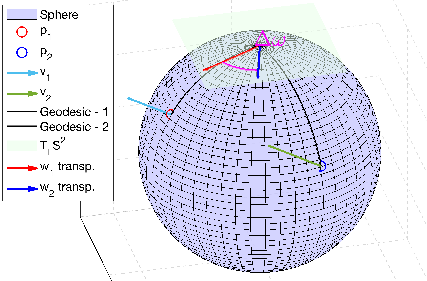
Figure 2: Illustration of angular velocity and acceleration for two points on a manifold, highlighting the geometric treatment of motion derivatives.

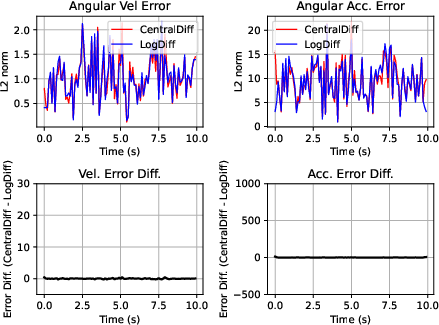
Figure 3: Comparison of log-central differencing and classical central differencing for angular acceleration estimation, demonstrating the efficacy of simple central differences given meaningful angular velocities.

Neural Distance Field Construction and Training

NRMF models the plausibility of poses, transitions, and accelerations using three neural fields, each trained to predict the geodesic distance to the closest example in the training dataset (AMASS). The training objective minimizes the discrepancy between the predicted distance and the true geodesic distance for each component, leveraging hierarchical networks and MLP decoders. Negative samples are generated via a mixed strategy combining Gaussian perturbations, random swaps, and fully random candidates, with nearest neighbor search accelerated using FAISS.

The learned fields enable efficient computation of Riemannian gradients for optimization and sampling, and the product manifold structure ensures interdependence between joints is respected, unlike prior works that treat joints independently.

Figure 4: Comparison of pose and transition distributions, visualized as spherical kernel density estimates for each joint, demonstrating the range of motion captured by NRMF.

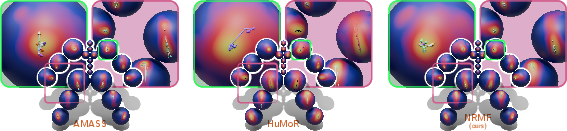
Figure 5: Transitions and accelerations overlaid onto pose distributions, illustrating the joint modeling of motion dynamics and the variability captured by NRMF.

Downstream Applications and Optimization Strategies

NRMF serves as a versatile generative prior for multiple tasks:

• Test-time optimization: Recovery of plausible motion sequences from 2D/3D observations via multi-stage optimization, incorporating pose, transition, and acceleration priors, as well as physics-based constraints (e.g., foot-floor contact).
• Motion generation and in-betweening: Sampling and denoising of motion trajectories using the geometric integrator, enabling robust interpolation between sparse keyframes and generation of diverse, lifelike motions.
• Motion refinement: Integration with regression-based mesh recovery pipelines (e.g., SMPLer-X) for post-hoc refinement, improving temporal consistency and physical plausibility.

The optimization pipeline is implemented in PyTorch, with loss terms balancing data fidelity, prior plausibility, and regularization. The geometric integrator is provided as pseudocode, ensuring reproducibility and extensibility.

Experimental Evaluation

Extensive experiments are conducted on AMASS, 3DPW, i3DB, EgoBody, and PROX datasets, covering tasks such as motion denoising, partial observation fitting, in-the-wild motion estimation, and motion generation. NRMF consistently outperforms state-of-the-art baselines (HuMoR, RoHM, MDM, PoseNDF, NRDF, DPoser, VPoser) across metrics including MPJPE, PA-MPJPE, acceleration error, contact plausibility, FID, and APD.

Key numerical results:

• On motion denoising, NRMF achieves the lowest positional and acceleration errors (MPJPE: 16.4mm, Acc Err: 2.25mm/s²), outperforming all baselines.
• For partial 3D observations, NRMF yields superior reconstruction of occluded joints and lower acceleration errors.
• In motion generation, NRMF attains the best FID for motion (5.317) and competitive diversity (APD: 96.37cm).
• In sparse keyframe in-betweening, NRMF achieves the lowest FID and acceleration errors, robustly interpolating missing frames.

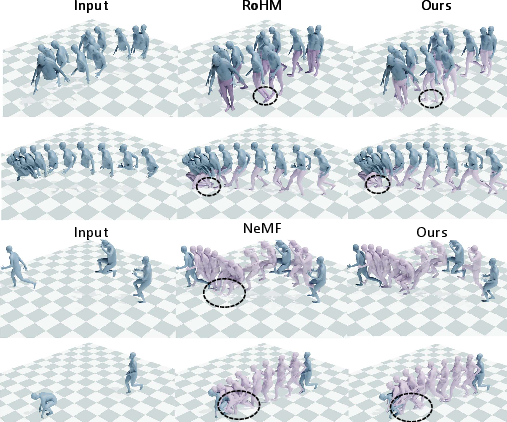
  Figure 6: Qualitative comparison with state-of-the-art methods on motion estimation from noisy partial observations and motion in-betweening.

  

  Figure 7: Qualitative comparison with state-of-the-art methods for in-the-wild motion estimation, highlighting anatomical accuracy and temporal consistency.

  

  Figure 8: Qualitative results on in-the-wild fitting on PROX, demonstrating robustness under occlusion.

  

  Figure 9: Qualitative results on downstream applications, including mesh recovery and motion interpolation.

  

  Figure 10: In-the-wild motion estimation on real-world videos, showing plausible and consistent motion recovery under challenging conditions.

Limitations and Future Directions

While NRMF provides strong inductive bias and superior performance, the iterative optimization incurs significant runtime (minutes per sequence), and the theoretical properties of the projected integrators remain to be fully characterized. Future work may explore learning-to-optimize strategies and principled sampling algorithms (e.g., Riemannian Langevin MCMC) to further improve efficiency and theoretical guarantees.

Conclusion

NRMF establishes a rigorous, geometry-aware framework for learning human motion priors, bridging the gap between data-driven and physically grounded modeling. By decomposing motion into pose, transition, and acceleration components and modeling their joint plausibility via neural distance fields, NRMF enables robust, temporally consistent, and physically plausible motion recovery and generation. The approach generalizes across modalities and tasks, consistently outperforming existing methods in both quantitative and qualitative evaluations. The geometric treatment of motion dynamics and the explicit modeling of higher-order derivatives represent a significant advancement in the field, with broad implications for animation, virtual reality, and human-computer interaction.