Performative Thinking? The Brittle Correlation Between CoT Length and Problem Complexity (2509.07339v1)

Abstract: Intermediate token generation (ITG), where a model produces output before the solution, has been proposed as a method to improve the performance of LLMs on reasoning tasks. While these reasoning traces or Chain of Thoughts (CoTs) are correlated with performance gains, the mechanisms underlying them remain unclear. A prevailing assumption in the community has been to anthropomorphize these tokens as "thinking", treating longer traces as evidence of higher problem-adaptive computation. In this work, we critically examine whether intermediate token sequence length reflects or correlates with problem difficulty. To do so, we train transformer models from scratch on derivational traces of the A* search algorithm, where the number of operations required to solve a maze problem provides a precise and verifiable measure of problem complexity. We first evaluate the models on trivial free-space problems, finding that even for the simplest tasks, they often produce excessively long reasoning traces and sometimes fail to generate a solution. We then systematically evaluate the model on out-of-distribution problems and find that the intermediate token length and ground truth A* trace length only loosely correlate. We notice that the few cases where correlation appears are those where the problems are closer to the training distribution, suggesting that the effect arises from approximate recall rather than genuine problem-adaptive computation. This suggests that the inherent computational complexity of the problem instance is not a significant factor, but rather its distributional distance from the training data. These results challenge the assumption that intermediate trace generation is adaptive to problem difficulty and caution against interpreting longer sequences in systems like R1 as automatically indicative of "thinking effort".

• The paper demonstrates that chain-of-thought lengths do not reliably indicate problem complexity, challenging prior claims of adaptive reasoning.
• Methodologically, transformer models are trained on grid-based mazes with A* traces, enabling precise comparison of in- and out-of-distribution performance.
• Key findings reveal excessive token generation on trivial problems and sensitivity to training distribution, calling for improved alignment of reasoning traces.

Analysis of the Correlation Between Chain-of-Thought Length and Problem Complexity in Transformer Reasoning Models

Introduction

This paper critically examines the widely held assumption that the length of intermediate reasoning traces—commonly referred to as Chain-of-Thought (CoT) sequences—generated by transformer-based reasoning models is indicative of problem complexity or computational effort. The authors train transformer models from scratch on derivational traces of the A* search algorithm in grid-based pathfinding domains, enabling precise control and measurement of problem difficulty. The paper reveals that the correlation between CoT length and problem complexity is brittle and largely dependent on the distributional similarity between training and test data, rather than reflecting genuine problem-adaptive computation.

Experimental Design and Methodology

The experimental setup leverages a $30 \times 30$ grid-based pathfinding domain, with mazes generated using a variety of algorithms (Wilson, Kruskal, DFS, Drunkard's Walk, Searchformer-style, and Free-space). The complexity of each problem instance is defined as the number of operations required by the A* algorithm to solve the maze, providing a ground-truth measure for comparison.

Transformer models (Qwen2.5 0.5B, modified to 380M parameters) are trained from scratch on 500,000 Wilson-generated mazes, with each training example including the problem description, the full A* trace, and the optimal plan. The models are evaluated on held-out Wilson mazes (in-distribution) and on mazes generated by other algorithms (out-of-distribution), as well as on trivial free-space problems with no obstacles.

Empirical Findings

Excessive CoT Length on Trivial Problems

Evaluation on free-space problems—where the optimal solution requires minimal computation—demonstrates that the model frequently produces excessively long reasoning traces, often reaching the maximum context limit of 32,000 tokens without generating a valid solution. Only 5 out of 100 free-space problems are solved correctly, and the scatter plot of generated trace length versus ground-truth A* trace length shows almost no alignment with the $y=x$ line.

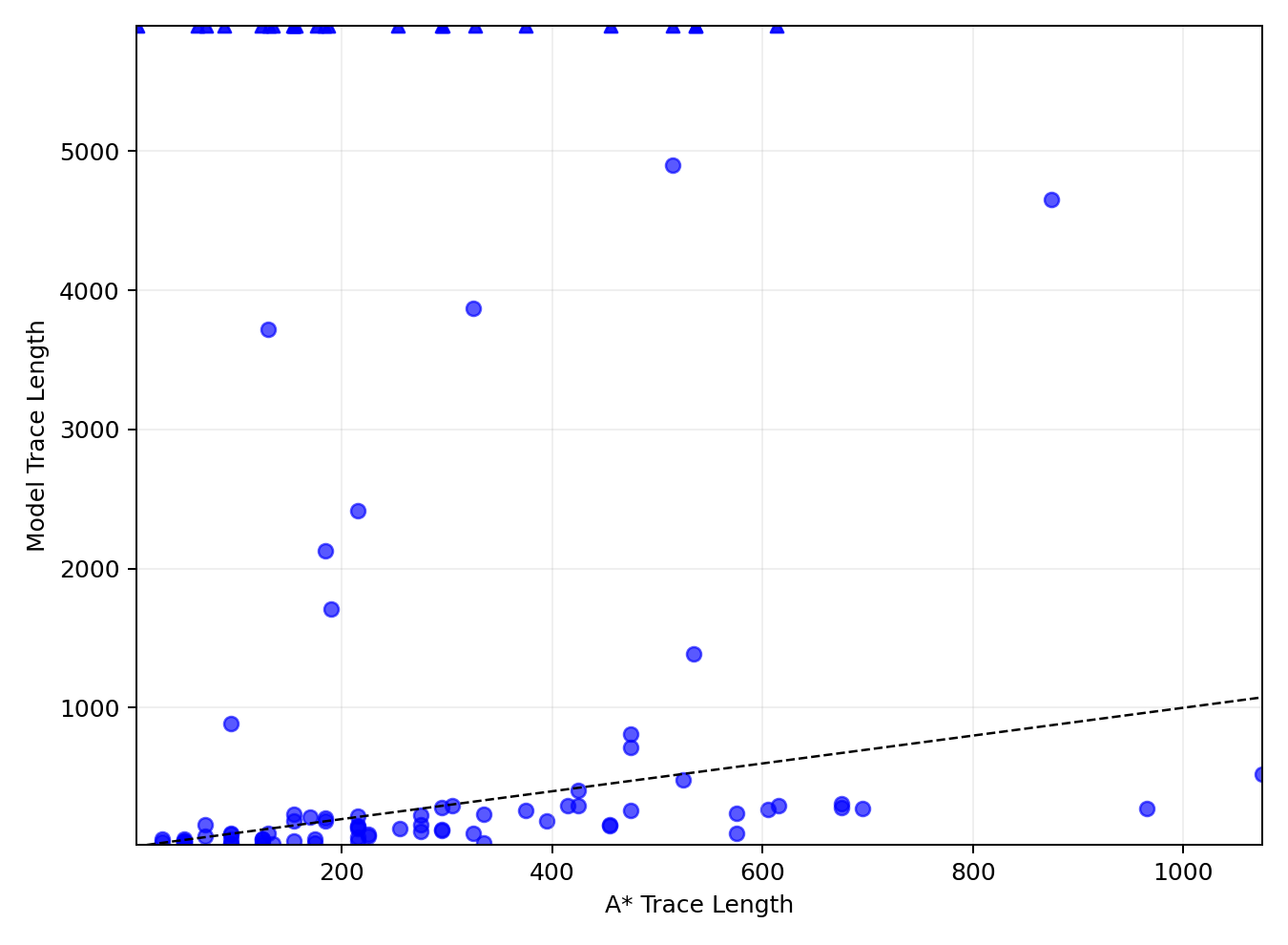
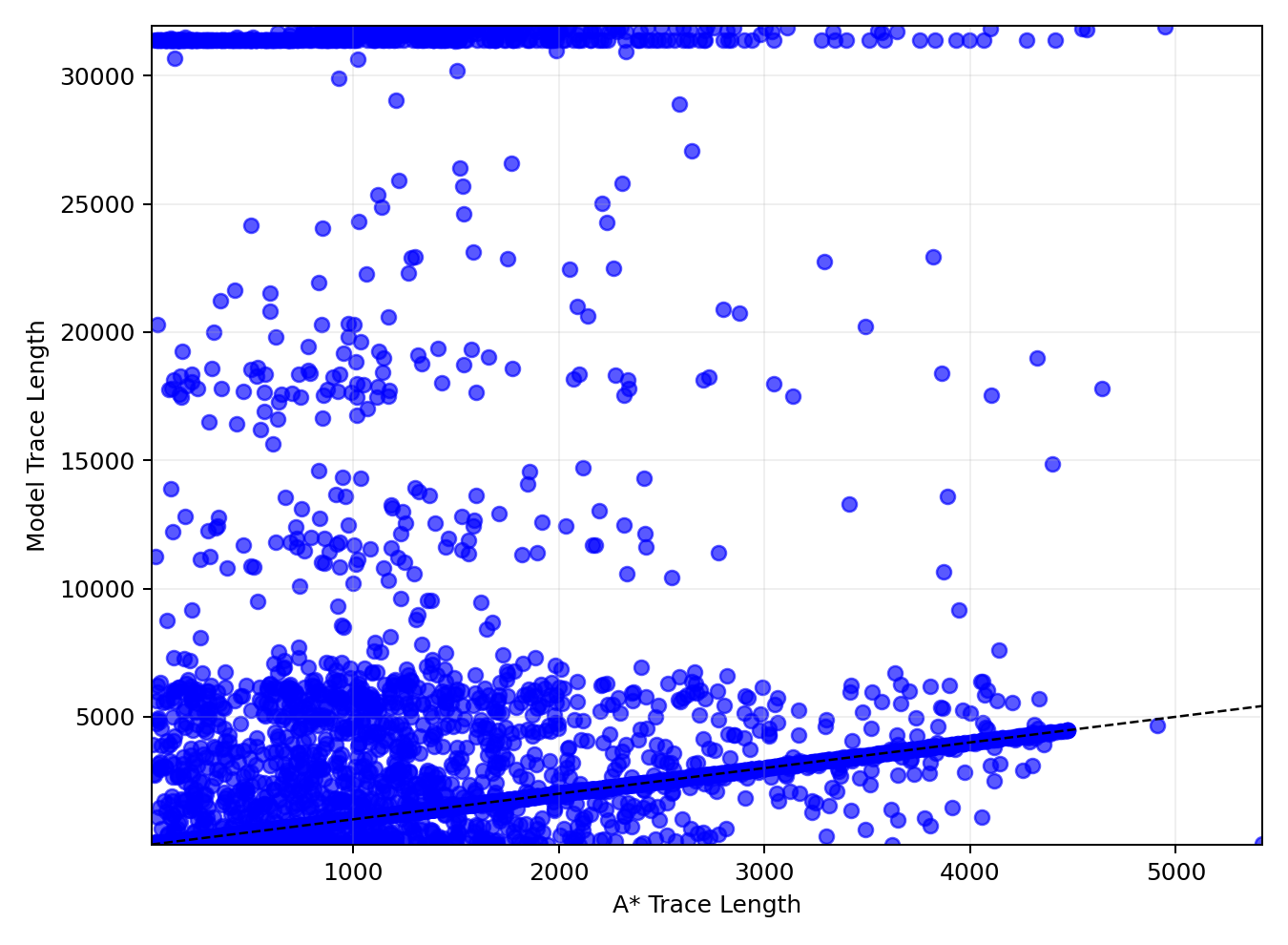
Figure 1: Responses on Free-space problems. Points at the top correspond to failures where the model generated tokens until reaching the 32k limit.

Figure 2: Example grid of a Free-space problem. It is a 30x30 grid with no obstacles in the inner grid. The start and goal states are chosen randomly.

Distributional Dependence of CoT Length

When evaluated on held-out Wilson mazes, the model's generated trace lengths show some alignment with ground-truth A* trace lengths, indicating a loose correlation. However, this correlation vanishes on mazes generated by structurally distinct algorithms (e.g., Searchformer-style, Drunkard's Walk), where the scatter plots reveal that intermediate trace lengths fluctuate independently of problem complexity.

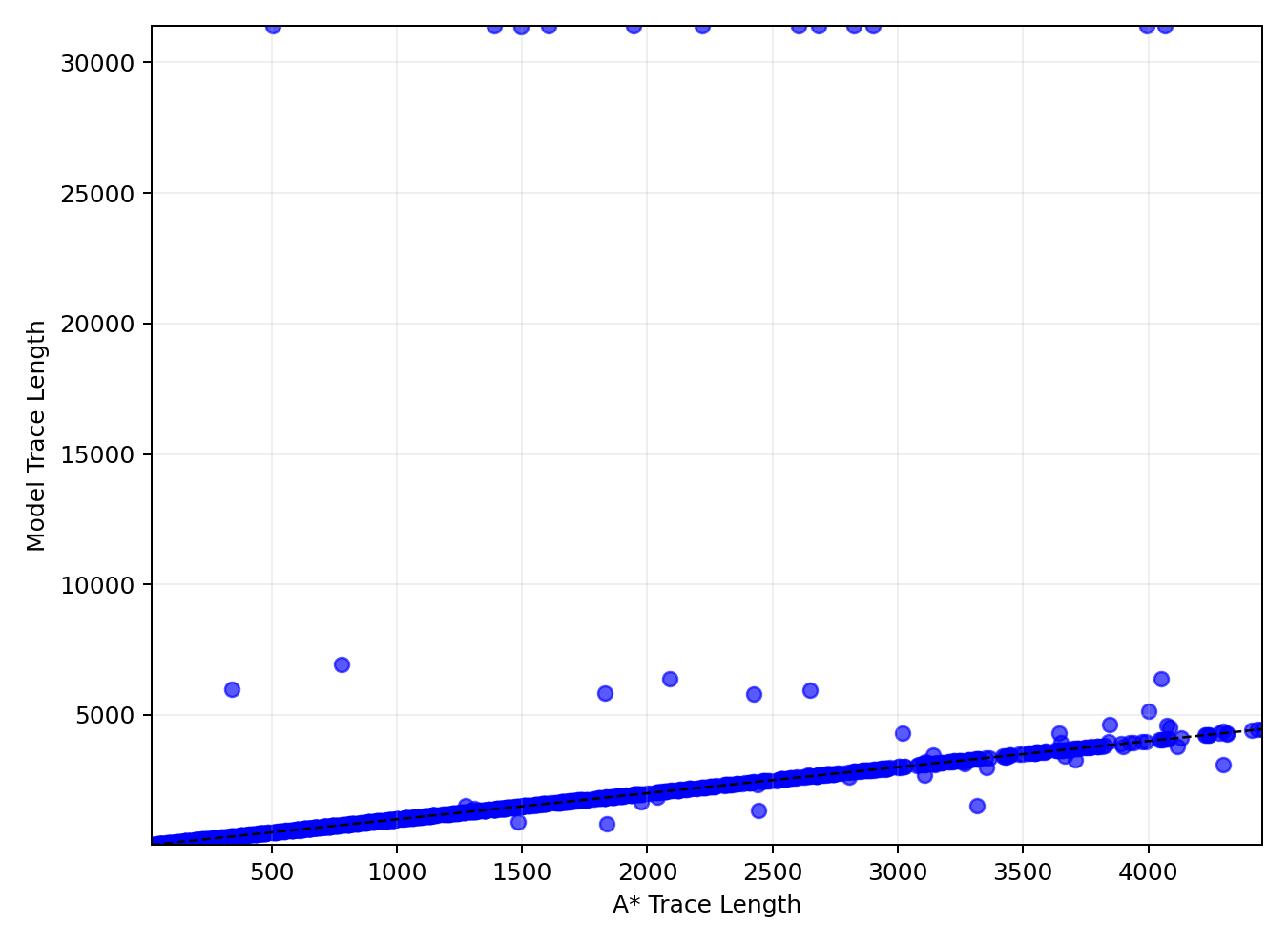
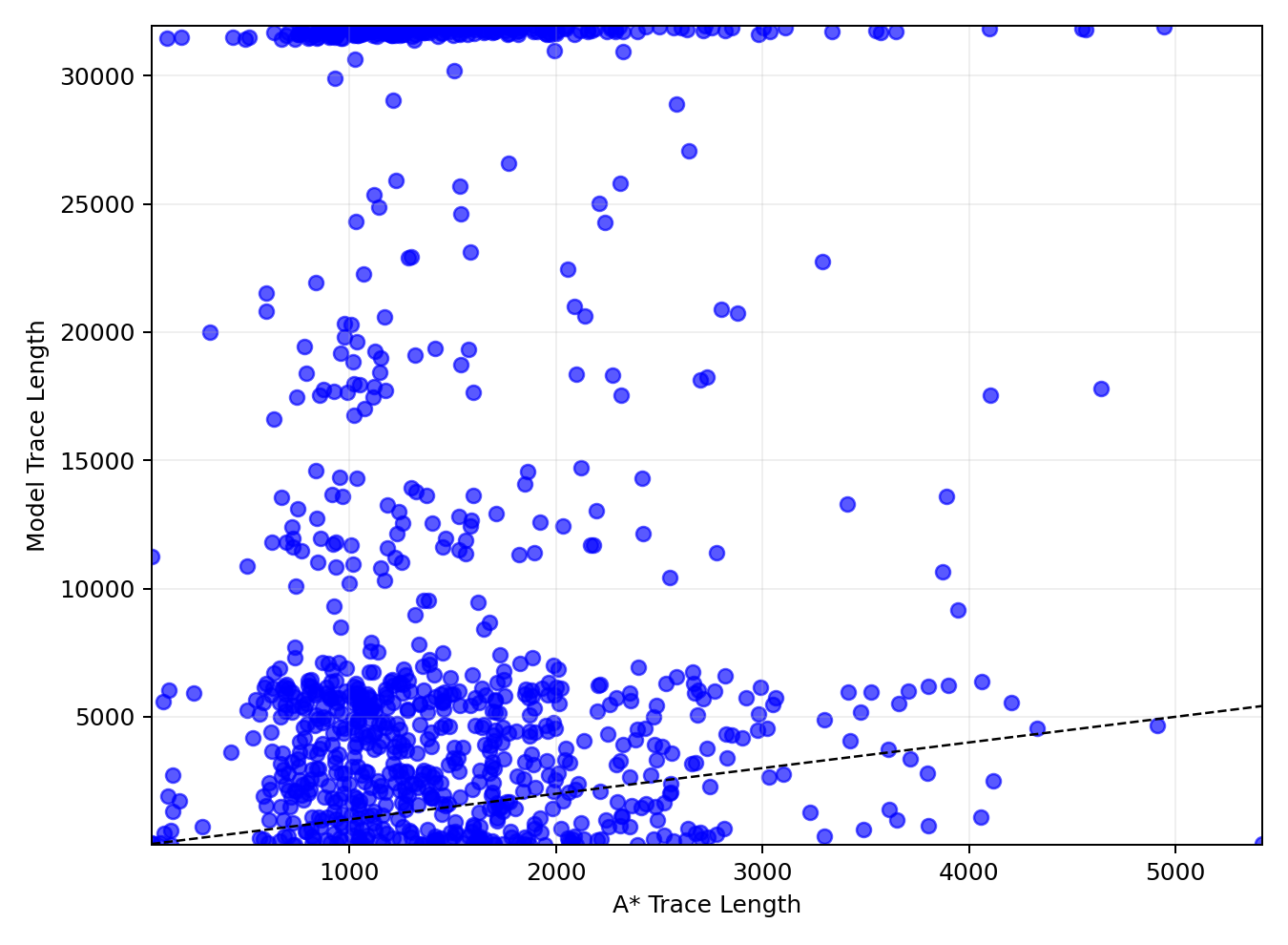
Figure 3: Wilson trace length scatter.

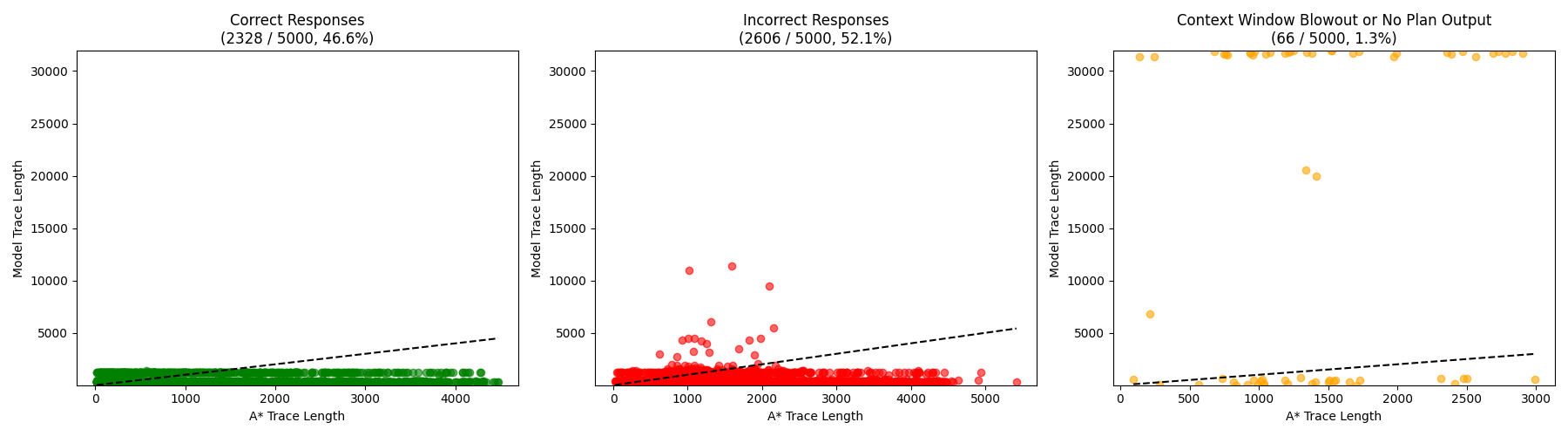
Figure 4: Caption.

This pattern suggests that the apparent adaptivity of CoT length is an artifact of approximate recall from the training distribution, rather than a reflection of problem-sensitive computation. The model's behavior is thus highly sensitive to the distributional distance between training and test instances.

Theoretical and Practical Implications

The results challenge the anthropomorphic interpretation of intermediate token generation as "thinking" or evidence of problem-adaptive computation. The lack of reliable correlation between CoT length and problem complexity, especially in out-of-distribution settings, undermines claims that longer reasoning traces indicate greater computational effort or efficiency. This has direct implications for research on efficient reasoning in LLMs, including methods that seek to optimize or truncate reasoning chains for improved performance or resource utilization.

The findings also highlight the limitations of current post-training methodologies, which typically apply optimization pressure only to the correctness of final outputs, leaving intermediate tokens unaligned with problem difficulty or structured reasoning. This calls for more rigorous approaches to interpreting and designing reasoning traces in transformer models.

Future Directions

The paper suggests several avenues for future research:

• Explicit Alignment of Reasoning Traces: Developing training objectives that directly align intermediate token generation with problem complexity or correctness, rather than relying on indirect supervision via final answers.
• Robustness to Distributional Shift: Investigating architectures and training regimes that enhance generalization and adaptivity of reasoning traces across diverse problem distributions.
• Mechanistic Interpretability: Extending mechanistic analyses to understand the internal representations and dynamics that give rise to reasoning traces, building on recent work in mechanistic interpretability of transformers.
• Evaluation Protocols: Establishing standardized benchmarks and evaluation protocols that account for distributional distance and problem complexity in assessing reasoning models.

Conclusion

This paper provides a rigorous analysis of the relationship between Chain-of-Thought length and problem complexity in transformer-based reasoning models. The evidence demonstrates that intermediate token length is only loosely correlated with problem difficulty and is primarily a function of distributional similarity to the training data. These findings caution against anthropomorphizing reasoning traces and underscore the need for more principled methodologies in the design and interpretation of reasoning processes in large language and reasoning models.