Large N Chern-Simons-matter fixed points with multiple flavors (2509.04565v1)

Abstract: In this paper we analyze the $2+1$d conformal fixed points arising from $SU(N_c)$ Chern-Simons-matter theories with multiple flavors $N_f > 1$ in the 't Hooft large $N_c$ limit. The multi-flavor generalization of quasi-fermionic theories (fermions or critical scalars coupled to Chern-Simons gauge fields) is straightforward, but this is not true for quasi-bosonic theories (scalars or critical fermions coupled to Chern-Simons gauge fields). The latter theories have three flavor-singlet relevant operators and also three marginal operators, that become exactly marginal for infinite $N_c$, but have a non-zero beta function at order $1/N_c$. We compute the beta functions of these couplings in various weak coupling limits, and discuss also their general structure, generalizing previous computations for $N_f=1$. We find that IR-stable fixed points of the marginal couplings exist for some values of $N_f$ and of the 't Hooft coupling $\lambda$, but not for other values, and in one case we can explicitly follow how two pairs of fixed points merge and disappear as $\lambda$ is increased. We also analyze the ``Semi-Critical'' conformal field theories that arise when fine-tuning two (rather than three) relevant operators, and compute the beta function for their (single) marginal coupling constant.

• The paper demonstrates that beta functions for flavor-singlet operators in quasi-bosonic theories are cubic polynomials, revealing distinct IR fixed points depending on Nf and the 't Hooft coupling.
• It employs planar diagrammatic analysis along with algebraic and topological methods to systematically compute beta functions and constrain the RG flow.
• Results indicate that while quasi-bosonic theories can exhibit IR-stable fixed points under certain Nf conditions, the fermionic formulations lack such stability, steering future research directions.

Large $N$ Chern-Simons-Matter Fixed Points with Multiple Flavors

Introduction and Theoretical Framework

This work provides a comprehensive analysis of $2+1$-dimensional conformal fixed points in $SU(N_c)$ Chern-Simons-matter theories with $N_f > 1$ flavors, focusing on the 't Hooft large $N_c$ limit. The paper distinguishes between quasi-fermionic and quasi-bosonic generalizations, emphasizing the nontrivial structure that arises in the multi-flavor quasi-bosonic case. The quasi-bosonic theories possess three relevant flavor-singlet operators and three marginal operators, which are exactly marginal at infinite $N_c$ but acquire nonzero beta functions at order $1/N_c$. The paper systematically computes these beta functions in various weak coupling limits and explores the existence and stability of IR fixed points as a function of $N_f$ and the 't Hooft coupling $\lambda$.

Operator Content and Marginal Coupling Structure

For $N_f > 1$, the quasi-bosonic theories exhibit a richer operator spectrum compared to the $N_f=1$ case. The singlet and adjoint scalar operators, denoted ${\cal O}_S$ and ${\cal O}_A$, have dimensions $\Delta = 1 + \mathcal{O}(1/N_c)$, leading to three relevant deformations: ${\cal O}_S$, ${\cal O}_S^2$, and ${\cal O}_A^2$. The marginal sector consists of three flavor-singlet six-scalar operators: ${\cal O}_S^3$, ${\cal O}_S {\cal O}_A^2$, and ${\cal O}_A^3$. At infinite $N_c$, these are exactly marginal, but for large finite $N_c$, their couplings run with beta functions of order $1/N_c$.

The beta functions for these couplings are cubic polynomials in the couplings, with universal cubic terms dictated by unitarity and the structure of planar diagrams. The analysis leverages both index and representation bases for the flavor contractions, with explicit transformation rules provided.

Computation of Beta Functions and Fixed Point Analysis

The beta functions are computed using effective actions for the auxiliary fields ($\zeta$ for fermions, $\sigma$ and $\zeta$ for bosons), integrating out matter fields and evaluating connected correlators up to five-point functions. The leading $1/N_c$ contributions are extracted from planar diagrams, with flavor structures classified according to their topologies.

Free Theory ($\lambda=0$) and Weak Coupling Expansion

At $\lambda=0$, the theory is free and the beta functions reduce to cubic polynomials in the couplings, with a degenerate fixed point at the origin. For small but finite $\lambda$, perturbative corrections split this degenerate fixed point, and the existence of IR-stable fixed points depends sensitively on $N_f$:

• For $N_f=2$ and $N_f \geq 5$, an IR-stable fixed point exists at small $\lambda$.
• For $N_f=3,4$, no IR-stable fixed point is found in the weak coupling regime.

The splitting and merging of fixed points as $\lambda$ is varied is analyzed using both algebraic and topological methods, including the Poincaré-Hopf index theorem and Bézout's theorem for polynomial systems.

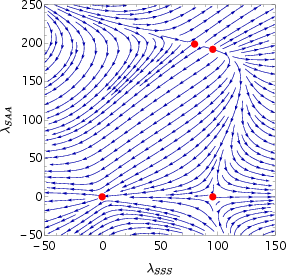
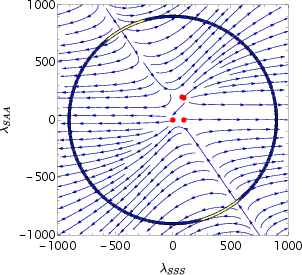
Figure 1: The flow to the IR of (minus) the beta function for the free boson theory, illustrating the fixed point structure for $N_f=2$.

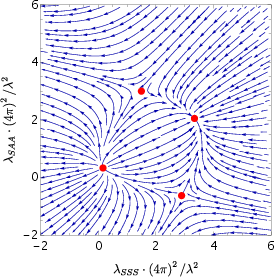
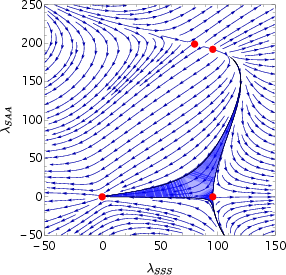
Figure 2: Left: Stream plot of flow to the IR of (minus) the beta function for small $\lambda_B$, showing the splitting of the degenerate fixed point and the emergence of an IR-stable fixed point.

Figure 3: Direction of the flow to the IR of (minus) the cubic term in the beta function, visualizing the universal behavior at large couplings for various $N_f$.

Large $N_f$ Limit and Scaling Laws

In the regime $1 \ll N_f \ll N_c$, the beta functions simplify, and the scaling of fixed points with $N_f$ is classified. The natural scaling $(2,1,0)$ for the couplings corresponds to the dominance of single-trace and double-trace operators in the large $N_f$ limit. The analysis reveals that the number and nature of fixed points can change discontinuously as $N_f$ increases, with critical values of $\lambda$ at which pairs of fixed points merge and disappear.

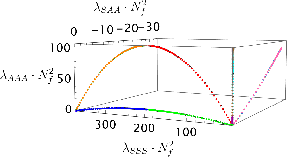
Figure 4: The fixed points of the beta function for the IR fixed point, showing the merging and disappearance of fixed points as $\lambda$ is increased in the large $N_f$ limit.

Fermionic Description and Absence of IR-Stable Fixed Points

In the weakly coupled fermionic description ($\lambda_F \to 0$), the beta functions are computed using parity arguments and explicit loop integrals. It is found that for all $N_f > 1$, there is no IR-stable fixed point, in contrast to the bosonic case. The fixed points come in parity pairs, and the origin is always a mixed fixed point.

Figure 5: Stream plot of the flow to the IR of (minus) the fermion beta functions, illustrating the absence of IR-stable fixed points for $N_f=2$.

Semi-Critical Theories

The paper also analyzes "Semi-Critical" theories, obtained by fine-tuning only two relevant operators. These theories have a single marginal coupling, whose beta function is again a cubic polynomial at order $1/N_c$. The existence of IR-stable fixed points in these theories depends on $N_f$ and the unknown coefficients in the five-point correlators. For the singlet Semi-Critical theory, an IR-stable fixed point exists for large enough $N_f$ at small $\lambda_B$, while for the adjoint Semi-Critical theory, the existence of IR-stable fixed points is more nuanced and depends on $N_f$ and the coupling regime.

Topological and Algebraic Constraints

The paper employs topological invariants (Poincaré-Hopf index) and algebraic geometry (Bézout's theorem) to constrain the possible behaviors of fixed points under continuous deformations of the couplings. Fixed points can only be created or annihilated in pairs, and the sum of indices is conserved under RG flow. The analysis of the flow at infinity provides further constraints on the global structure of the RG flows.

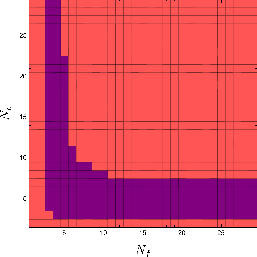
Figure 6: Existence of a weakly coupled IR-stable point for different values of $N_c \geq 2$ and $N_f \geq 1$, showing the regions in parameter space where IR-stable fixed points exist.

Implications and Future Directions

The results have significant implications for the landscape of non-supersymmetric conformal field theories in three dimensions, especially in the context of large $N$ dualities and holography. The existence and disappearance of IR-stable fixed points as a function of $N_f$ and $\lambda$ suggest rich phase structures and possible fixed-point mergers, which may be relevant for condensed matter systems and the paper of quantum criticality.

The formalism developed allows for the computation of beta functions at leading order in $1/N_c$ for arbitrary $N_f$, and the methods can be extended to theories with both scalars and fermions, including supersymmetric cases. The analysis also highlights the importance of higher-point correlators (especially the five-point function) in determining the existence of fixed points, motivating further computational efforts in this direction.

Conclusion

This work provides a detailed and systematic paper of the fixed point structure in large $N$ Chern-Simons-matter theories with multiple flavors, uncovering new phenomena in the RG flow and establishing rigorous constraints on the existence and stability of conformal fixed points. The interplay between algebraic, topological, and diagrammatic methods yields a robust framework for analyzing multi-coupling RG flows in vector-like gauge theories. Future research directions include the computation of higher-point correlators, exploration of the strongly coupled regime, and generalization to mixed scalar-fermion theories and supersymmetric extensions.