Predictions of the Nancy Grace Roman Space Telescope Galactic Exoplanet Survey. III. Detectability of Giant Exomoons of Wide Separation Giant Planets (2509.03492v1)

Abstract: The Nancy Grace Roman Space Telescope (Roman) will conduct a Galactic Exoplanet Survey (RGES) to discover bound and free-floating exoplanets using gravitational microlensing. Roman should be sensitive to lenses with mass down to ~ 0.02 $M_{\oplus}$, or roughly the mass of Ganymede. Thus the detection of moons with masses similar to the giant moons in our Solar System is possible with Roman. Measuring the demographics of exomoons will provide constraints on both moon and planet formation. We conduct simulations of Roman microlensing events to determine the effects of exomoons on microlensing light curves, and whether these effects are detectable with Roman. We focus on giant planets from 30 $M_{\oplus}$ to 10 $M_{Jup}$ on orbits from 0.3 to 30 AU, and assume that each planet is orbited by a moon with moon-planet mass ratio from $10^{-4}$ to $10^{-2}$ and separations from 0.1 to 0.5 planet Hill radii. We find that Roman is sensitive to exomoons, although the number of expected detections is only of order one over the duration of the survey, unless exomoons are more common or massive than we assumed. We argue that changes in the survey strategy, in particular focusing on a few fields with higher cadence, may allow for the detection of more exomoons with Roman. Regardless, the ability to detect exomoons reinforces the need to develop robust methods for modeling triple lens microlensing events to fully utilize the capabilities of Roman.

• The paper demonstrates a simulation-based method using custom inverse ray-shooting to model triple lens microlensing events for exomoon detection.
• The paper finds that under conservative assumptions, Roman is expected to detect about one giant exomoon, with the yield sensitive to survey cadence and moon properties.
• The paper highlights the role of caustic structure, alignment effects, and survey strategy in enhancing the detectability of exomoons in microlensing events.

Detectability of Giant Exomoons of Wide-Separation Giant Planets with the Roman Space Telescope

Introduction and Motivation

The paper presents a comprehensive simulation-based analysis of the detectability of giant exomoons orbiting wide-separation giant planets via gravitational microlensing in the upcoming Nancy Grace Roman Space Telescope Galactic Exoplanet Survey (RGES). The motivation stems from the ubiquity of massive moons around Solar System giant planets and the lack of confirmed exomoon detections to date. Roman's sensitivity to lens masses down to $\sim 0.02~M_\oplus$ (Ganymede-like) enables the possibility of detecting exomoons with masses and orbital architectures analogous to those in the Solar System. The work aims to quantify Roman's exomoon yield, characterize the phenomenology of microlensing signals from planet-moon-star triple lens systems, and assess the impact of survey strategy and cadence on detection rates.

Microlensing Formalism and Triple Lens Modeling

The authors review the microlensing formalism for single, binary, and triple lens systems, emphasizing the complexity introduced by the addition of a moon to a planet-star lens. The lens equation for $N_l$ point masses is solved numerically, with triple lens systems requiring inversion of a tenth-order polynomial. The caustic topology is classified into close, resonant, and wide regimes, with the planetary caustic location and size determined by the planet-star mass ratio $q_p$ and separation $s_p$.

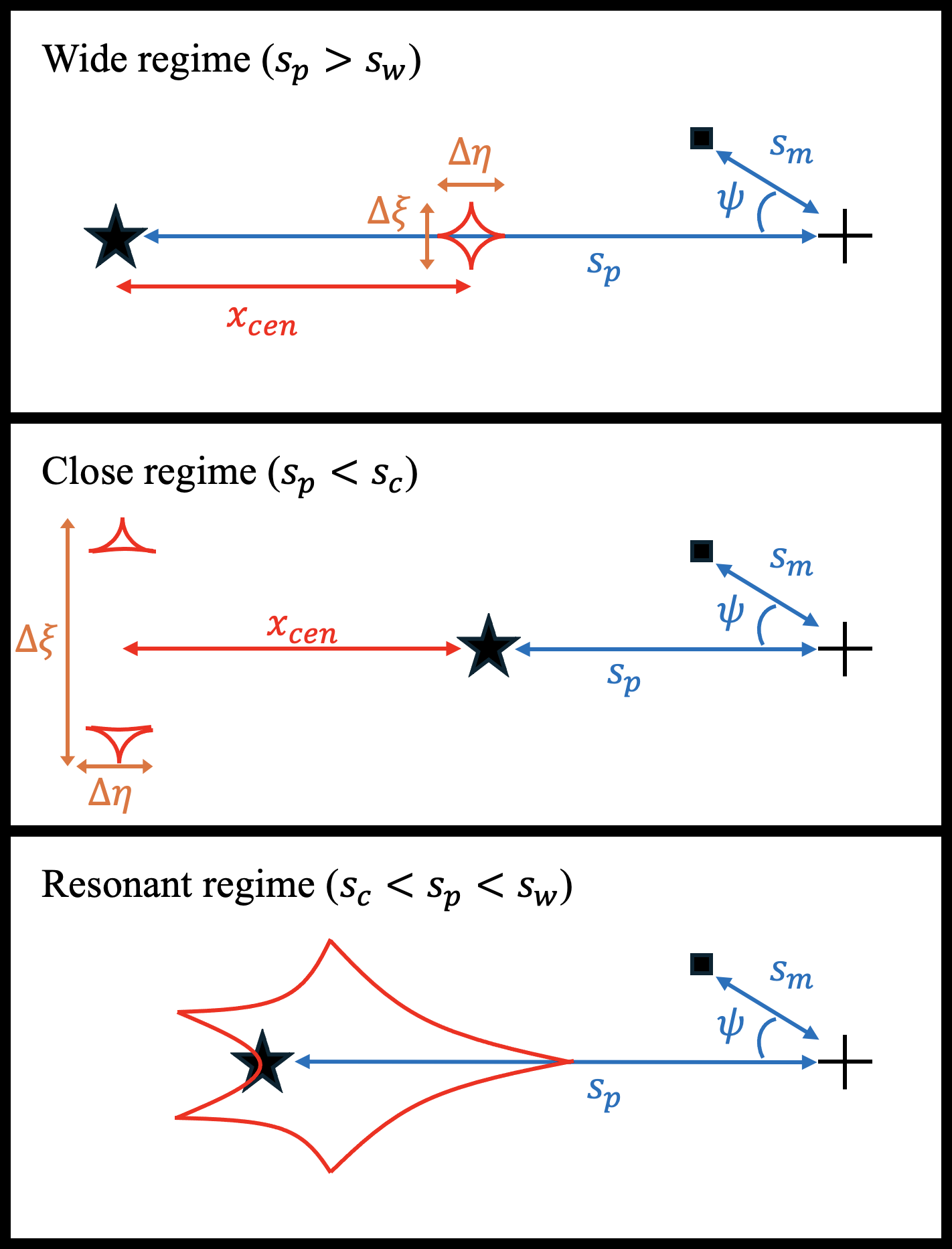
Figure 1: Geometry of lens systems and their caustics for different caustic topologies, illustrating the spatial relationships between star, planet, and moon.

To compute light curves with finite source effects, the authors develop a custom image-centered inverse ray-shooting algorithm, as existing public triple lens codes are numerically unstable for the low mass ratios ($q_m \sim 10^{-4}$) relevant to exomoons. The algorithm efficiently computes magnification maps in the vicinity of planetary caustics, adding the analytic single-lens magnification for the unperturbed image. Verification against binary lens models shows numerical noise is negligible compared to photometric uncertainties.

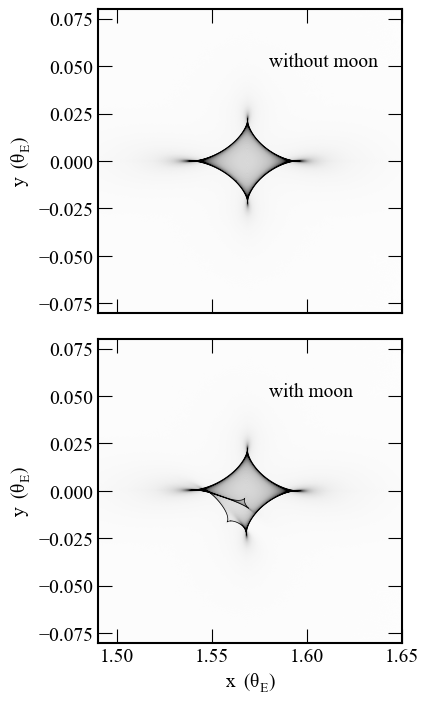
Figure 2: Example magnification map for a planet-moon-star system, showing additional caustic structure introduced by the moon.

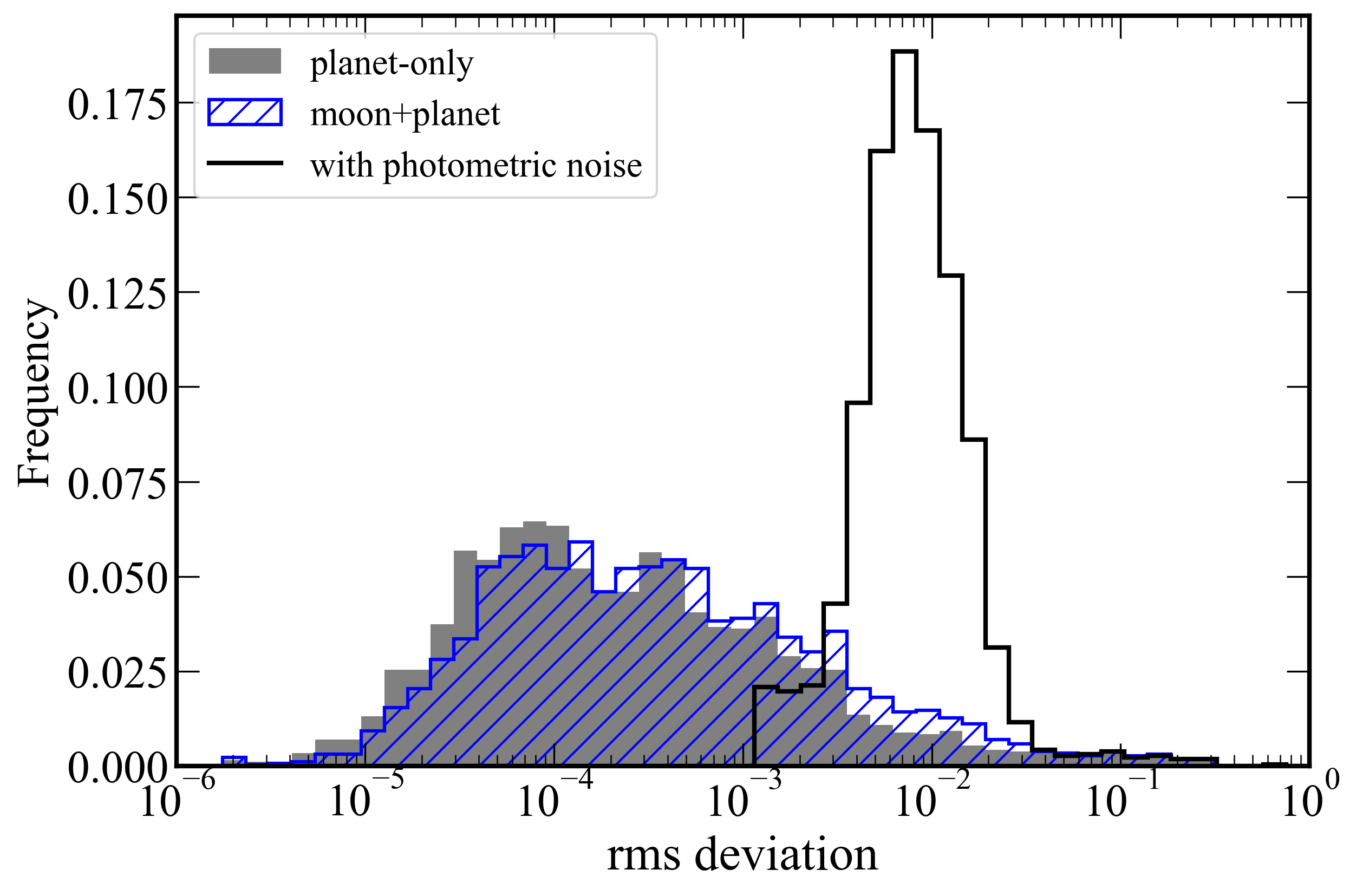
Figure 3: Histogram of rms deviation between light curves computed with the custom ray-shooting algorithm and MulensModel, demonstrating negligible numerical noise.

Physical and Statistical Considerations

The detectability of exomoons depends on the interplay between the Hill radius $a_{\rm Hill}$, the planetary Einstein ring radius $R_{E,p}$, and the caustic cross-section $s_{caus}$. The authors simulate moons with mass ratios $q_m$ from $10^{-4}$ to $10^{-2}$ and semimajor axes $a_m$ from $0.1$ to $0.5~a_{\rm Hill}$, focusing on giant planets ($30~M_\oplus$ to $10~M_{\rm Jup}$) with wide orbits ($0.3$ to $30$ AU). The planet mass function is adopted from microlensing constraints, and the moon population is normalized to one moon per planet.

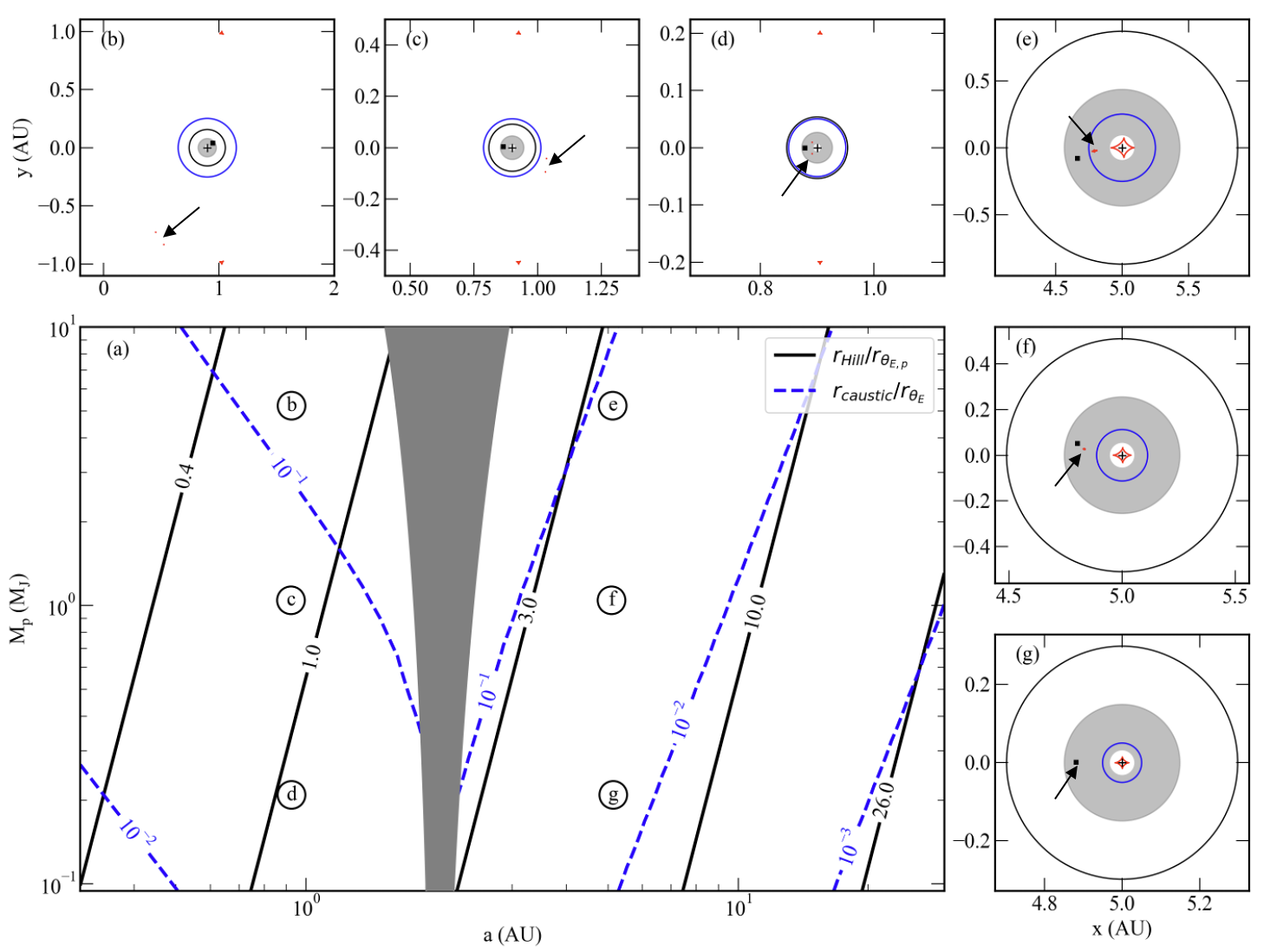
Figure 4: Range of simulated planet masses and semimajor axes, with contours of constant $s_{\rm Hill}$ and $s_{caus}$, and example planet-moon systems.

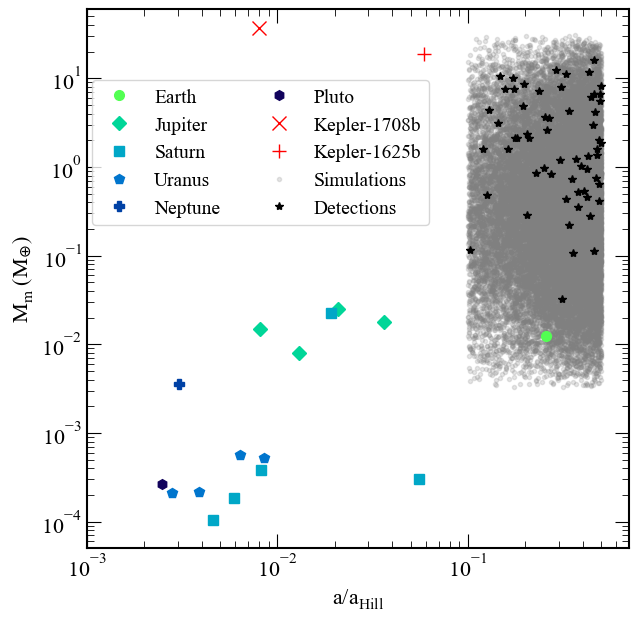
Figure 5: Masses and semimajor axes of simulated moons compared to Solar System moons and exomoon candidates.

Roman Survey Simulations and Detection Criteria

The simulation pipeline uses the GULLS tool to generate realistic microlensing events with Roman's photometric noise model and Galactic stellar population. Detected planetary events are injected with moons, and triple lens light curves are computed near the planetary caustic. Detection is defined by a $\Delta\chi^2$ threshold between planet-only and planet+moon fits, with a conservative value of $\Delta\chi^2_m > 90$.

Results: Exomoon Yield and Signal Phenomenology

The main result is that, under the adopted assumptions, Roman is expected to detect of order one giant exomoon over the full RGES survey. The yield is sensitive to the assumed moon population, survey duration, and cadence. Detected moons are typically $\gtrsim 0.2~M_\oplus$ and orbit planets with $a_p \gtrsim 1$ AU and $q_p \gtrsim 10^{-3}$. The detection probability is nearly independent of $a_m/a_{\rm Hill}$, with a bias toward moons around wider-orbit planets due to larger Hill radii.

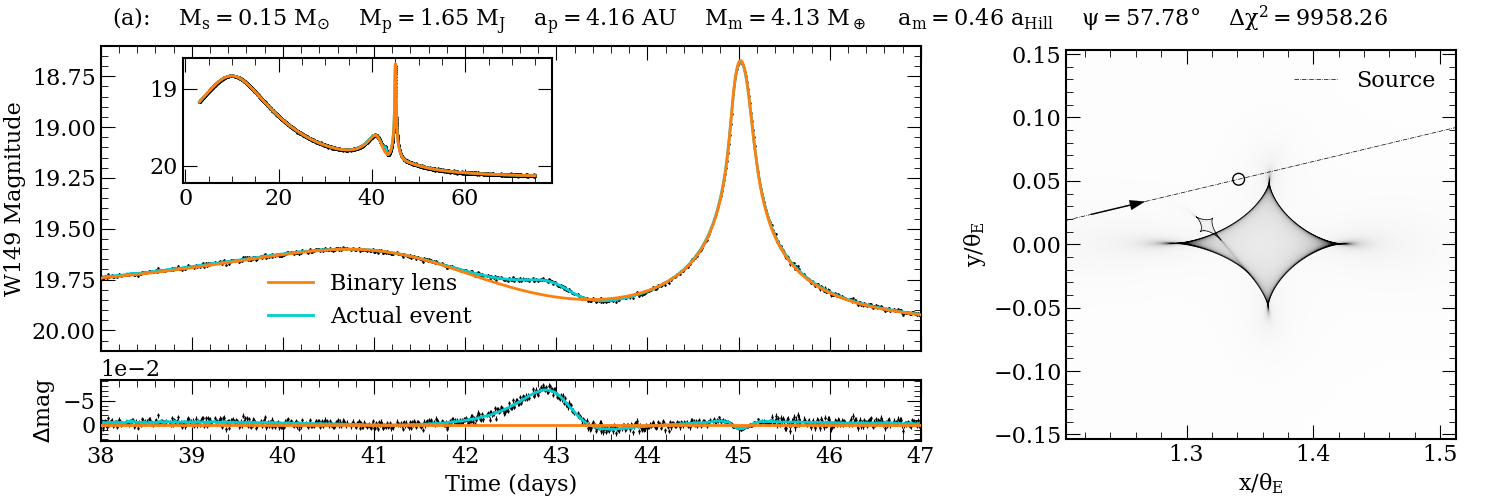
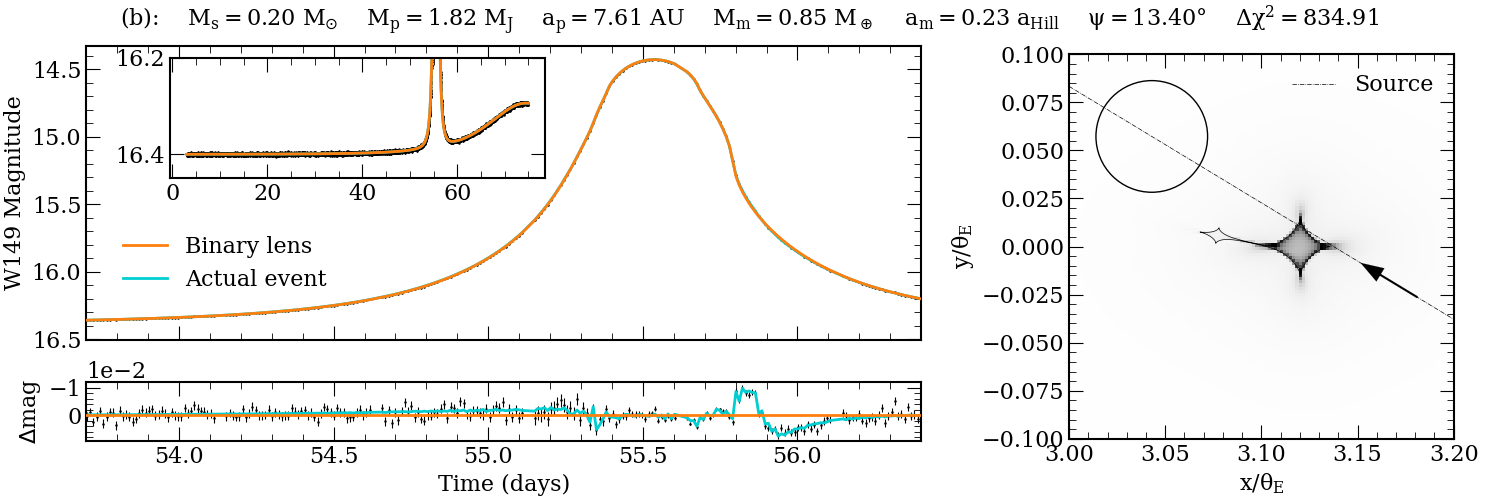
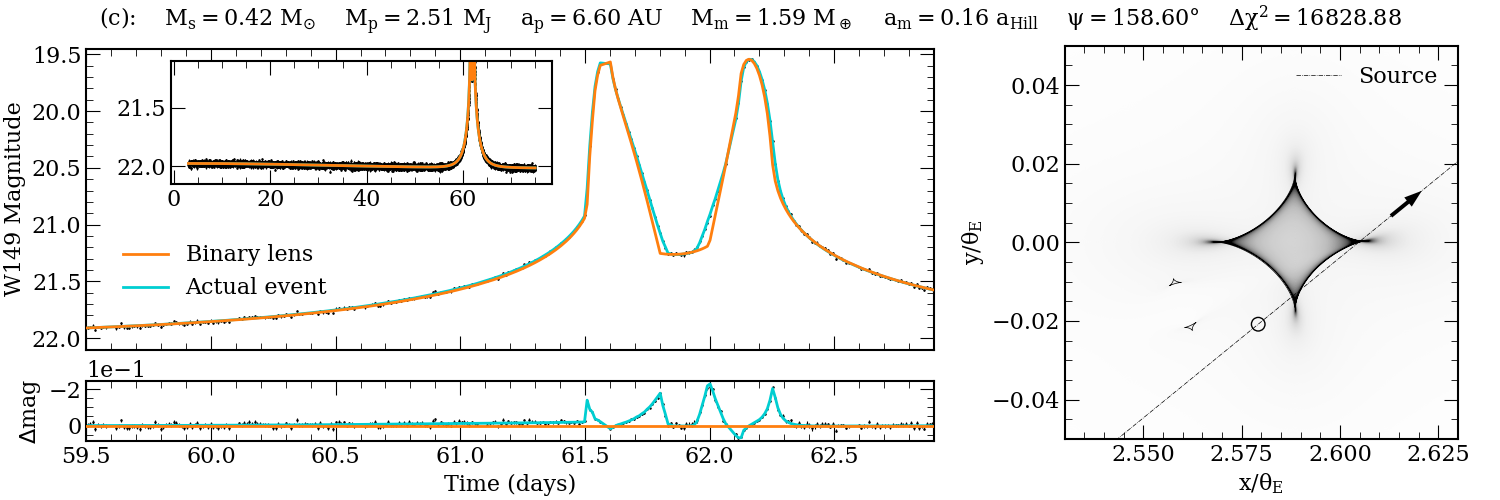
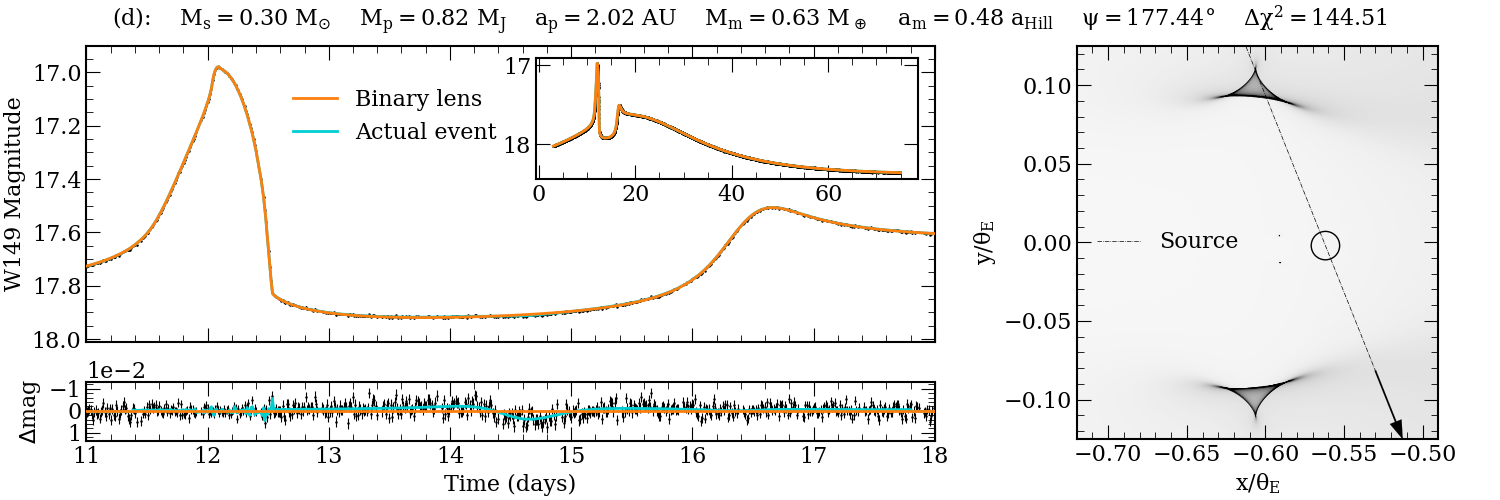
Figure 6: Example simulated Roman light curves with detectable moons, illustrating diverse perturbation morphologies.

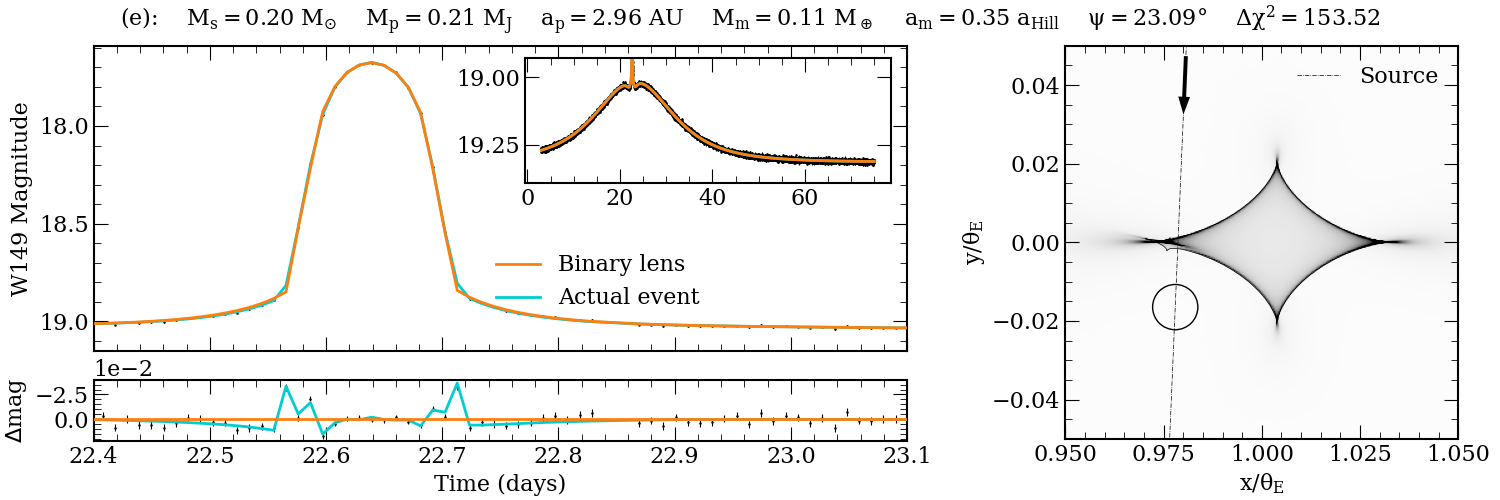
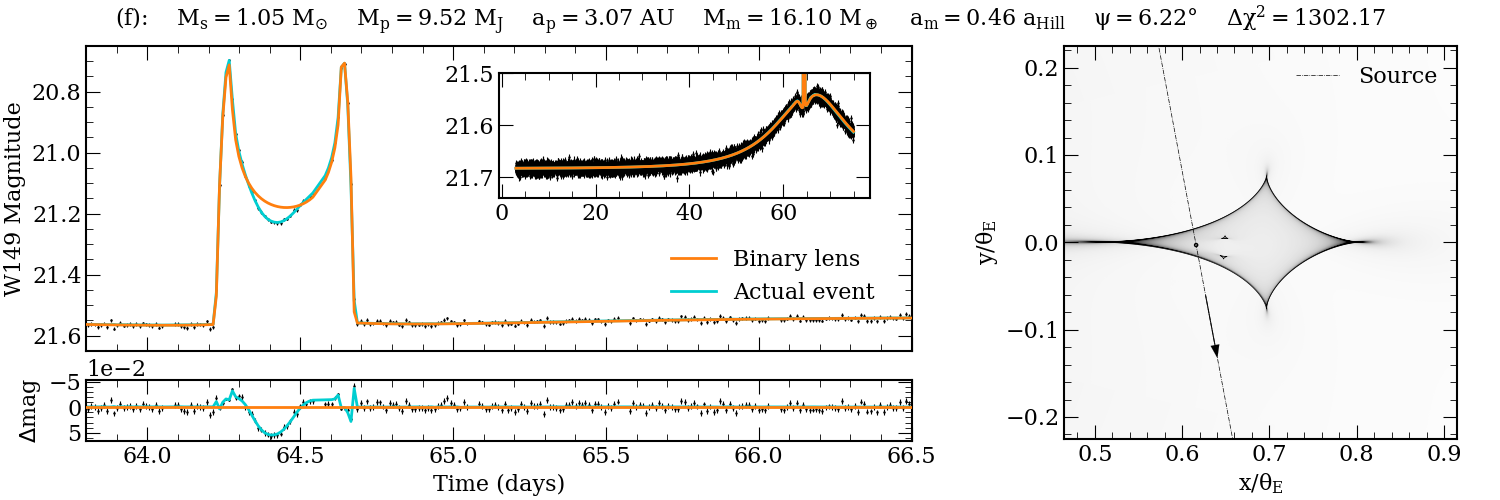
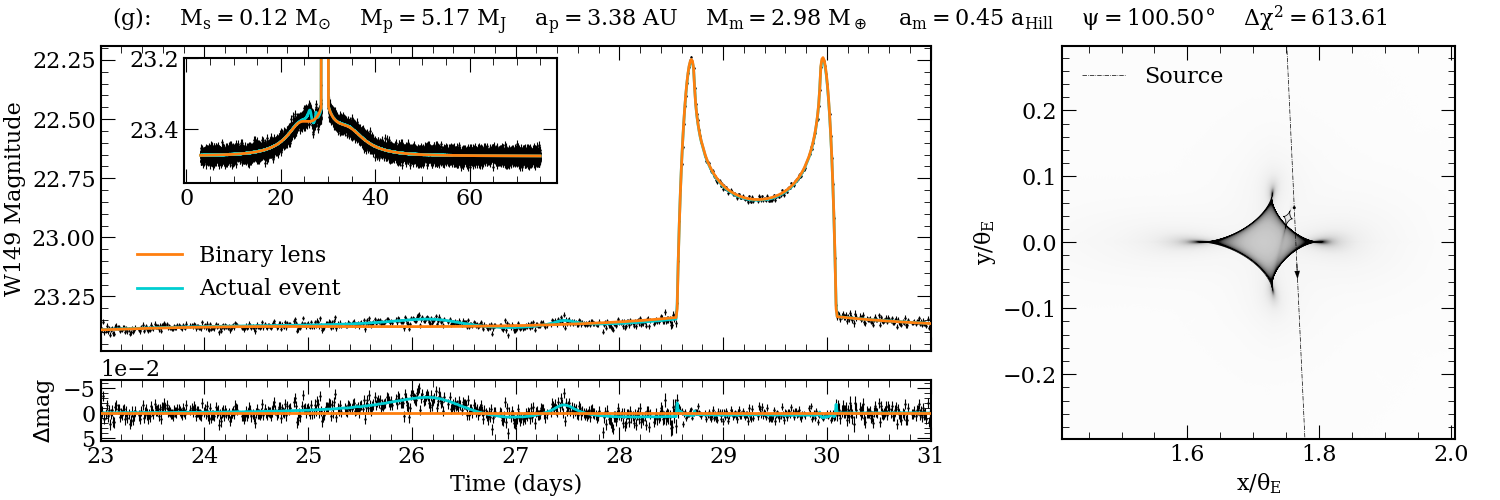
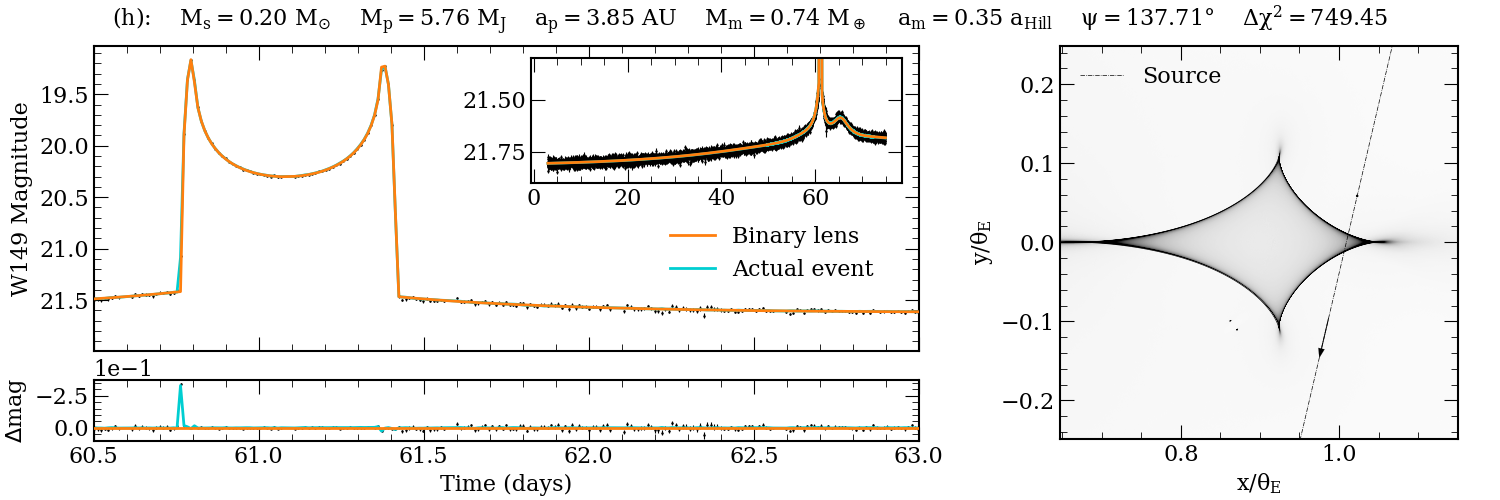
Figure 7: Detailed light curve and magnification map for a detected exomoon event, showing residuals and caustic structure.

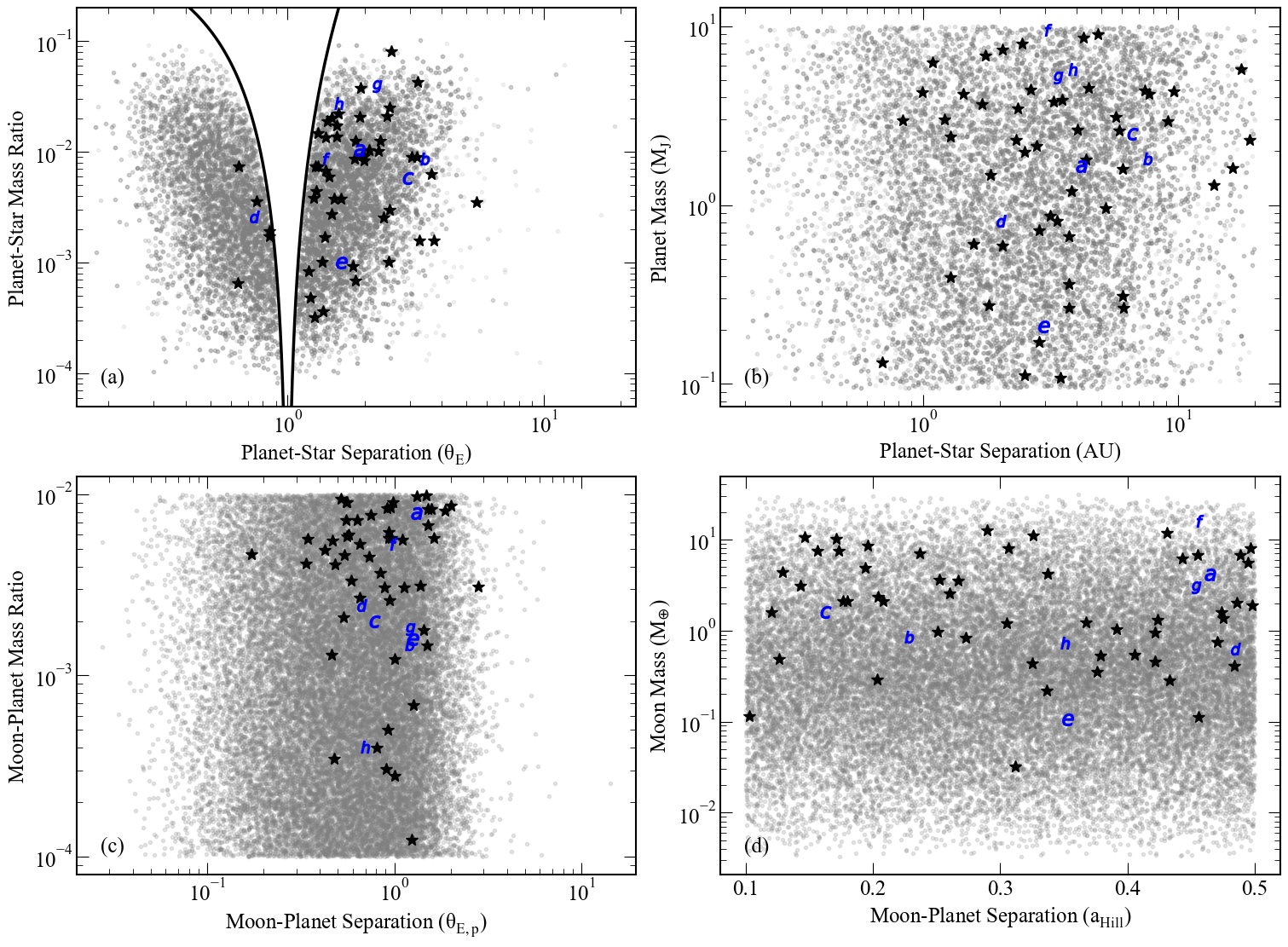
Figure 8: Physical parameters of simulated events with and without detected moons, highlighting the regions of parameter space with successful detections.

Figure 9: Histograms of simulated and detected events as a function of planet and moon parameters, showing the yield distribution.

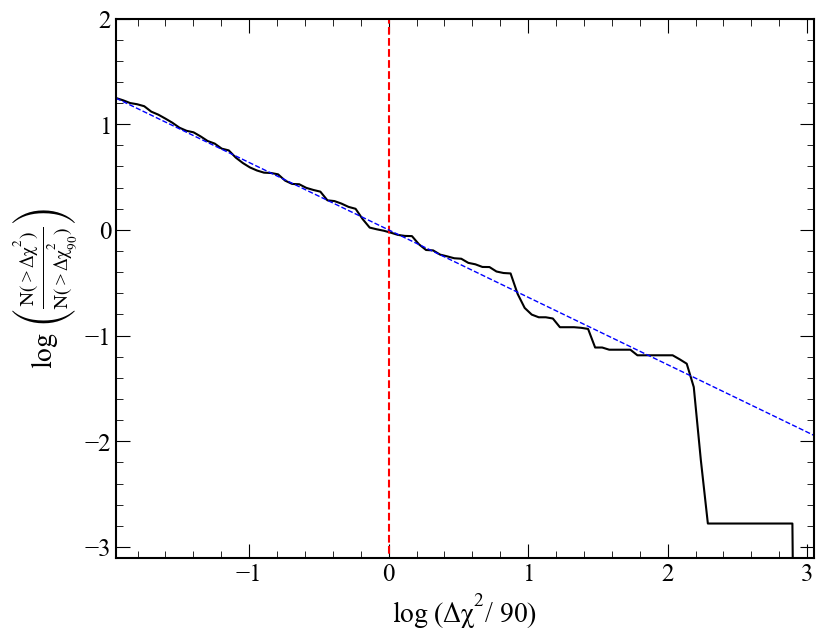
Figure 10: Cumulative distribution of detected moons as a function of $\Delta\chi^2$ threshold, fit by a power law.

Two primary detection channels are identified: (1) direct caustic perturbations when the source crosses the lunar caustic, and (2) subtle distortions of the planetary caustic that cannot be reproduced by binary lens models. The latter channel is analogous to circumbinary planet detections via caustic deformation.

Survey Strategy and Cadence Optimization

A key finding is that the cumulative distribution of $\Delta\chi^2$ for moon detections follows a power law with slope $\alpha \approx 0.64$. Increasing the survey cadence linearly increases $\Delta\chi^2$ and thus the yield, with a factor of 10 cadence improvement yielding $\sim 4.6\times$ more exomoon detections, assuming photometric uncertainties are unchanged.

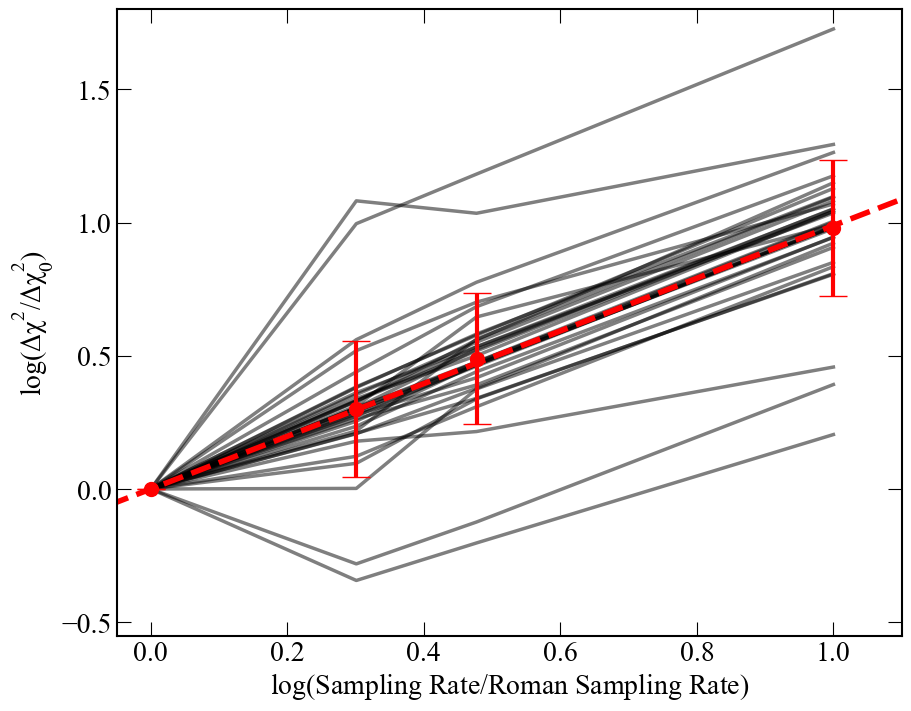
Figure 11: Improvement in $\Delta\chi^2$ for detected moons as a function of sampling rate, demonstrating linear scaling.

Multiple Moons and Caustic Complexity

The authors simulate systems with multiple moons, finding that the probability of detection increases with the number of moons due to increased caustic coverage. However, complex caustic interactions may suppress or enhance individual moon signals, motivating further paper.

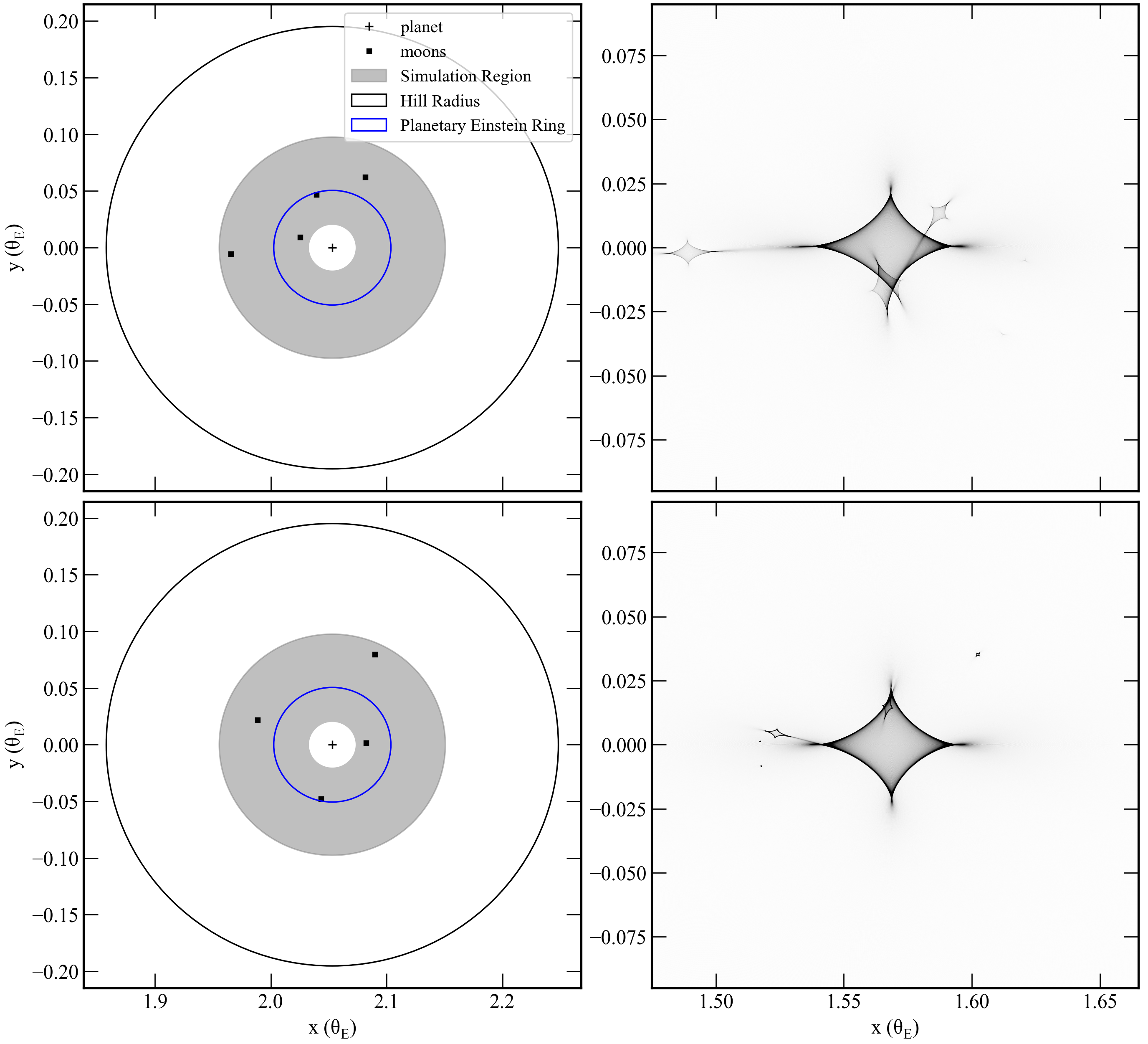
Figure 12: Magnification maps for planetary systems with four moons, showing increased caustic complexity and detection cross-section.

Caustic Alignment Effects

Detection probability is enhanced when the moon's projected separation is aligned or anti-aligned with the planet-star axis, due to constructive interference of gravitational shear from the star and planet.

Figure 13: Change in caustic structure as a function of moon orientation angle $\Psi$, illustrating alignment effects on caustic size.

Limitations and Future Directions

The exclusion of resonant caustic events and central caustic perturbations is a computational necessity, but may underestimate the true exomoon yield. Orbital motion of moons is shown to be negligible for the typical event timescales. The authors highlight the need for robust, efficient triple lens light curve codes and fitting algorithms, as well as expanded simulations for other moon architectures (e.g., Earth-Moon analogs).

Conclusion

This work provides a rigorous assessment of the detectability of giant exomoons with the Roman Space Telescope via microlensing. The predicted yield is low under conservative assumptions, but can be increased with survey optimization or if exomoons are more common or massive than in the Solar System. The paper establishes the phenomenological diversity of exomoon microlensing signals and the critical role of survey cadence. The results reinforce the necessity for advanced triple lens modeling and fitting techniques to fully exploit Roman's capabilities. Future work should address the detectability of lower-mass moons, resonant caustic events, and the development of scalable algorithms for triple and higher-order lens systems. The implications for exomoon demographics and planet formation theory are significant, and Roman's survey will provide the first statistical constraints on the population of giant exomoons in the Galaxy.