On anomalies and fermionic unitary operators (2509.02989v1)

Abstract: We point out that fermionic unitary operators which anticommute among themselves appear in various situations in quantum field theories with anomalies in the Hamiltonian formalism. To illustrate, we give multiple derivations of the fact that position-dependent $U(1)$ transformations of two-dimensional theories with $U(1)$ symmetry of odd level are fermionic when the winding number is odd. We then relate this mechanism to the anomalies of the discrete $\mathbb{Z}_N \subset U(1)$ symmetry, whose description also crucially uses unitary operators which are fermionic. We also show that position-dependent $SU(2)$ transformations of four-dimensional theories with $SU(2)$ symmetry with Witten anomaly are fermionic and anticommute among themselves when the winding number is odd.

• The paper demonstrates that the anticommutation of localized fermionic operators underpins the distinction between anomalies in bosonic and fermionic systems.
• It provides explicit constructions for U(1), Zₙ, and SU(2) symmetries, deriving unique commutator maps and cocycle classifications using differential cohomology.
• The findings offer a unified Hamiltonian framework for diagnosing anomalies, with implications for SPT phases, edge modes, and gauging obstacles in quantum field theories.

Fermionic Unitary Operators and Anomalies in Quantum Field Theory

This paper provides a comprehensive analysis of the role of fermionic unitary operators in the manifestation of anomalies within quantum field theories (QFTs), focusing on the Hamiltonian formalism. The authors systematically demonstrate that the anticommutation of localized symmetry operators is a key mechanism underlying the distinction between anomalies in bosonic and fermionic systems. The work covers three principal cases: $U(1)$ symmetry in two dimensions, $Z_n$ discrete symmetry as a subgroup of $U(1)$, and $SU(2)$ symmetry in four dimensions with Witten anomaly.

---

Locality and Anticommutation in Fermionic QFTs

The central observation is that, in fermionic QFTs, unitary operators $U_1$ and $U_2$ representing symmetry transformations localized in disjoint regions may anticommute, i.e., $U_1 U_2 = - U_2 U_1$, in contrast to the strictly commuting case in bosonic theories. This anticommutation is directly linked to the possibility of odd-level anomalies in fermionic systems, which are forbidden in bosonic systems.

---

$U(1)$ Symmetry in Two Dimensions: Operator Construction and Commutator Map

The authors analyze the $U(1)$ symmetry with level $k$ in two dimensions, where the charge density operator $J^t(x)$ satisfies

$$[J^t(x), J^t(y)] = k \frac{i}{2\pi} \frac{\partial}{\partial y} \delta^{(\text{P})}(x-y).$$

They construct position-dependent symmetry operators

$$U(f) = \exp\left(2\pi i \int_{S^1} f(x) J^t(x) dx\right),$$

where $f$ is a function on $S^1$ with winding number $w_f$. The commutator map for these operators is derived as

$$(f,g) = \frac{k}{2} \left( \int_0^{2\pi} [f(x) g'(x) - g(x) f'(x)] dx + f(0) w_g - w_f g(0) \right).$$

This formula is shown to be unique under locality, bi-additivity, and alternating conditions.

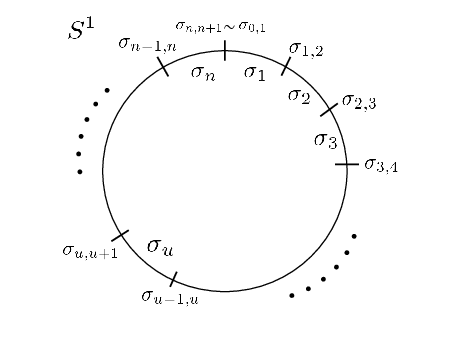
Figure 1: The patching of $S^1$ with multiple intervals $\sigma_u$ and points $\sigma_{u,u+1}$, used in the regularized construction of $U(f)$.

A key result is that for odd $k$ and odd winding number, $U(f)$ is fermionic and anticommutes with other such operators supported on disjoint regions. This is the operator-theoretic origin of the restriction that bosonic QFTs only admit even $k$.

---

Anomalies of Discrete $Z_n$ Symmetry via Embedding in $U(1)$

The anomaly structure of discrete $Z_n$ symmetry is analyzed by embedding $Z_n \subset U(1)$ and constructing explicit fusion operators at the boundaries of regions where symmetry is applied. The anomaly is encoded in a 3-cocycle $\alpha(a,b,c)$, which for $U(1)$ level $k$ is given by

$\alpha(a, b, c) = \frac{k}{2} \frac{a}{n} p(b,c),$

where $p(b,c)$ is the carry function in modular arithmetic. The fermion parity data $\nu(b,c) = k\, p(b,c)$ controls the graded commutativity of the fusion operators.

Figure 2: The profile and auxiliary functions used in the analysis of the anomaly of $Z_n\subset U(1)$.

This construction recovers the known group cohomology classification for bosonic anomalies and the supercohomology extension for fermionic anomalies, with explicit operator-theoretic realization.

---

$SU(2)$ Symmetry in Four Dimensions and the Witten Anomaly

The paper extends the analysis to four-dimensional theories with $SU(2)$ symmetry. The Witten anomaly is shown to manifest as the anticommutation of position-dependent $SU(2)$ symmetry operators $U(f)$ and $U(g)$ with winding number one, localized in disjoint regions:

$U(f) U(g) = - U(g) U(f).$

This is derived using the theory of invertible phases and $\eta$-invariants, with the bulk five-dimensional configuration encoding the anomaly.

Figure 3: The 5d configuration employed for the analysis of position-dependent $SU(2)$ transformations, with nontrivial gauge fields localized in disjoint regions.

The result provides a Hamiltonian perspective on the obstruction to gauging $SU(2)$ in the presence of the Witten anomaly, as no state in the Hilbert space can be invariant under all such unitary operators.

---

Mathematical Formalism: Differential Cohomology and Quadratic Refinement

The authors connect the commutator map to the graded-commutative product in differential cohomology, showing that the anomaly is a quadratic refinement of the pairing in $\hat H^1(S^1)$. The explicit formula for the commutator map is shown to be closely related to the Cheeger-Simons differential character pairing, with the difference between bosonic and fermionic cases arising from the quadratic refinement required by spin structure.

---

Implications and Future Directions

The operator-theoretic approach presented in this work provides a unified framework for understanding anomalies in both bosonic and fermionic QFTs, with direct implications for the classification of SPT phases, the structure of symmetry-protected edge modes, and the obstruction to gauging anomalous symmetries. The explicit construction of fermionic unitary operators and their commutation relations offers a concrete method for diagnosing anomalies in lattice and continuum models.

The connection to invertible phases and differential cohomology suggests further avenues for generalization to higher-form symmetries and non-invertible symmetry structures. The formalism is also amenable to numerical and algebraic implementation in the paper of topological phases and quantum computation.

---

Conclusion

This paper rigorously establishes the role of fermionic unitary operators in the manifestation of anomalies in QFTs, providing explicit operator constructions, commutator maps, and cohomological classifications for $U(1)$, $Z_n$, and $SU(2)$ symmetries. The results clarify the operator-theoretic origin of the distinction between bosonic and fermionic anomalies and offer a robust framework for future investigations into symmetry and topology in quantum systems.