Hitchhiker's Guide to the Swampland: The Cosmologist's Handbook to the string-theoretical Swampland Programme (2509.02632v1)

Abstract: String theory has strong implications for cosmology: it tells us that we cannot have a cosmological constant, that single-field slow-roll inflation is ruled out, and that black holes decay. We elucidate the origin of these statements within the string-theoretical swampland programme. The swampland programme is generating a growing body of insights that have yet to be incorporated into cosmological models. Taking a cosmologist's perspective, we highlight the relevance of swampland conjectures to black holes, dark matter, dark energy, and inflation, including their implications for scalar fields such as quintessence and axions. Our goal is to inspire cosmological model builders to examine the compatibility of effective field theories with quantum gravitational UV completions and to address outstanding cosmological tensions such as the Hubble tension. This comprehensive literature review presents clear definitions, cosmological implications, and the current status - including evidence and counterexamples - of the following swampland conjectures: the anti-de Sitter distance conjecture (AdSDC), the completeness conjecture (CC), the cobordism conjecture, the de Sitter conjecture (dSC), the swampland distance conjecture (SDC), the emergence proposal (EP), the Festina Lente Bound (FLB), the finite number of massless fields conjecture (or finite flux vacua conjecture (FFV)), the no global symmetries conjecture, the no non-supersymmetric theories conjecture, the non-negative null energy condition conjecture, the positive Gauss-Bonnet term conjecture, the species scale conjecture, the gravitino swampland conjecture (GSC), the tadpole conjecture, the tameness conjecture, the trans-Planckian censorship conjecture (tPCC/TCC), the unique geodesic conjecture, and the weak gravity conjecture (WGC), including the repulsive force conjecture (RFC).

• The paper provides a systematic mapping of major swampland conjectures and discusses their implications for inflation, dark energy, and dark matter models.
• It employs a detailed review of string theory constructions and semiclassical gravity arguments to highlight methodological advances and practical challenges in effective field theory.
• The review emphasizes observational prospects and suggests the need for multi-field or non-standard inflation scenarios to reconcile theory with emerging cosmological data.

Comprehensive Review of "Hitchhiker's Guide to the Swampland: The Cosmologist's Handbook to the string-theoretical Swampland Programme"

The paper provides an extensive and systematic review of the string-theoretic swampland programme, with a focus on its implications for cosmology. It catalogues the major swampland conjectures, their interrelations, and their consequences for cosmological model building, including inflation, dark energy, dark matter, and black hole physics. The work is notable for its technical depth, its critical assessment of the conjectures' status, and its emphasis on the practical challenges of applying these ideas to real-world cosmological scenarios.

---

The Swampland Programme: Structure and Motivation

The swampland programme aims to delineate the subset of effective field theories (EFTs) that can arise as low-energy limits of consistent quantum gravity (QG) theories, particularly string theory. The "landscape" comprises those EFTs that are consistent with quantum gravity, while the "swampland" consists of apparently consistent EFTs that cannot be UV-completed into a theory of quantum gravity. The boundary between these sets is conjectured to be defined by a set of "swampland conjectures," which are motivated by string theory constructions, black hole physics, holography, and general QG consistency arguments.

The paper emphasizes that these conjectures are not proven theorems but are supported by a combination of string vacua surveys, semiclassical gravity arguments, and the absence of counterexamples. The conjectures are interdependent, forming a tightly connected web (see Figure 1), and their mutual consistency is a nontrivial constraint on the space of possible EFTs.

---

Key Swampland Conjectures and Their Cosmological Implications

The review systematically presents the major swampland conjectures, providing precise definitions, cosmological consequences, and the current status of evidence and counterexamples. The most impactful conjectures for cosmology are discussed below.

1. Swampland Distance Conjecture (SDC)

The SDC posits that traversing a trans-Planckian distance in scalar field space leads to the emergence of an infinite tower of states with exponentially decreasing masses:

$$m(\phi) \sim m_0 \exp(-\mathfrak{a} d(\phi, \phi_0))$$

with $\mathfrak{a} = \mathcal{O}(1)$. This constrains the field range in inflationary and quintessence models to be sub-Planckian, typically $\Delta\phi \lesssim \mathcal{O}(1) M_P$.

Implications:

• Large-field inflation is generically in tension with the SDC, as it requires super-Planckian field excursions.
• Quintessence models for dark energy are constrained to small field ranges, limiting the class of viable potentials.
• The SDC predicts the appearance of light towers (e.g., Kaluza-Klein or string states) near infinite distance limits, which can have observable consequences in the dark sector.

2. de Sitter Conjecture (dSC) and its Refinements

The dSC asserts that scalar potentials in quantum gravity must satisfy

$$\frac{|\nabla V|}{V} \geq \frac{\mathfrak{s}_1}{M_P}$$

with $\mathfrak{s}_1 = \mathcal{O}(1)$, or, in the refined version, that either this holds or the minimum eigenvalue of the Hessian satisfies

$$\min(\nabla_i \nabla_j V) \leq -\frac{\mathfrak{s}_2}{M_P^2} V$$

with $\mathfrak{s}_2 = \mathcal{O}(1)$. The combined version (see Figure 1) interpolates between these conditions.

Implications:

• Stable or metastable de Sitter vacua are ruled out, challenging the existence of a cosmological constant and simple slow-roll inflation.
• Single-field slow-roll inflation and eternal inflation are generically excluded for $\mathcal{O}(1)$ values of the parameters.
• Dark energy must be dynamical (quintessence-like), with a time-dependent equation of state.
• Many popular inflationary models (Starobinsky, natural inflation, etc.) are in tension with the dSC unless additional mechanisms (e.g., warm inflation, multi-field dynamics, brane-world scenarios) are invoked.

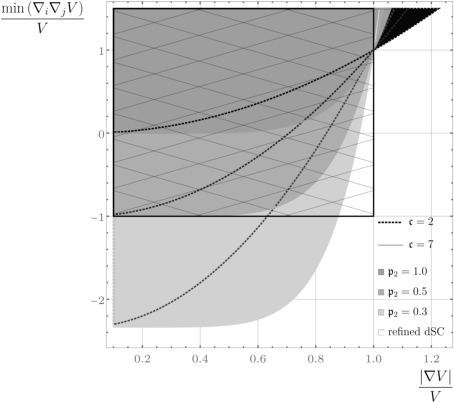
  Figure 2: The parameter space of the refined and combined de Sitter conjectures, showing the overlap and differences in the allowed regions for $(\mathfrak{s}_1, \mathfrak{s}_2)$. The shaded regions are excluded ("swampland") for different choices of the combined conjecture parameters.

3. Anti-de Sitter Distance Conjecture (AdSDC)

The AdSDC generalizes the SDC to AdS vacua, stating that as $V \to 0^-$, a tower of states becomes light with

$$m \lesssim |V|^{\mathfrak{d}} M_P^{1-2\mathfrak{d}}$$

with $\mathfrak{d} \sim \mathcal{O}(1)$. This implies that AdS and dS vacua are separated by infinite distance in moduli space.

Implications:

• Cosmological models that interpolate between AdS and dS (e.g., sign-changing cosmological constant) are in the swampland.
• The conjecture motivates the "dark dimension" scenario, where the smallness of the cosmological constant is linked to the existence of a mesoscopic extra dimension, with phenomenological consequences for dark matter and black hole physics.

  Figure 3: Schematic illustration of moduli space with and without a potential. The geodesic distance between two points increases when the potential restricts the accessible subspace.

4. Weak Gravity Conjecture (WGC)

The WGC requires that gravity is the weakest force, i.e., there exists a particle with charge-to-mass ratio $q/m \geq 1/M_P$. This has multiple forms (electric, magnetic, scalar, etc.) and is tightly connected to the absence of global symmetries and the completeness of the charge spectrum.

Implications:

• The WGC constrains axion decay constants, ruling out large-field axion inflation unless alignment or multi-axion mechanisms are invoked.
• The conjecture implies that black holes must be able to decay, forbidding stable remnants and supporting the cobordism conjecture.

5. Species Scale Conjecture (SSC)

The SSC posits that the cutoff of an EFT coupled to gravity is lowered by the number of light species:

$\Lambda_S = M_P / N_S^{1/(d-2)}$

This has implications for the validity of EFTs in the early universe and during inflation.

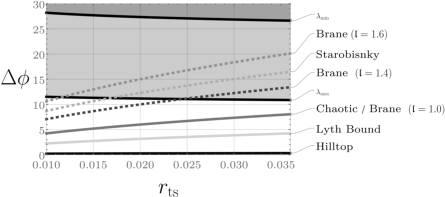
Figure 4: Upper and lower bounds on the maximal field range for various inflationary models, derived from the species scale and observational constraints on the tensor-to-scalar ratio.

---

Interrelations and the Swampland Web

The paper emphasizes the intricate web of relations among the conjectures. For example:

• The SDC and dSC are linked via the emergence of light towers at infinite distance, which destabilize dS vacua.
• The WGC, completeness conjecture, and no global symmetries conjecture are mutually reinforcing, with implications for the existence of magnetic monopoles and the absence of global charges.
• The cobordism conjecture, which posits that the bordism group of QG is trivial, underpins the uniqueness of quantum gravity and the absence of stable black hole remnants.

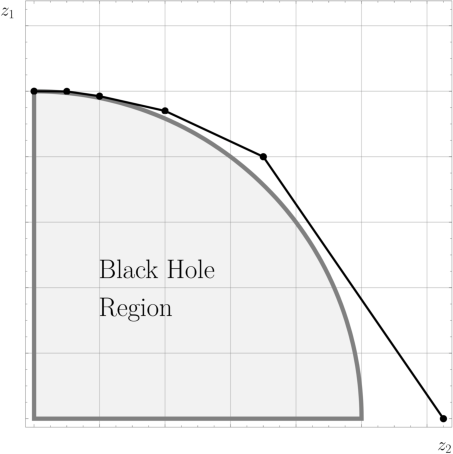
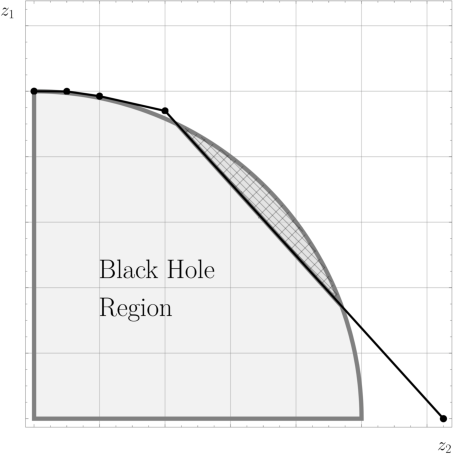
Figure 5: Illustration of the convex hull conjecture and its violation in compactifications with small extra dimensions, highlighting the emergence of superextremal Kaluza-Klein modes.

---

Critical Assessment and Observational Status

The review is careful to note that most conjectures are best justified in the asymptotic regions of moduli space, while cosmology typically probes the "bulk." This raises questions about the applicability of the conjectures to real-world cosmology. The paper documents numerous cases where cosmological models are in tension with the conjectures for $\mathcal{O}(1)$ parameters, but would be allowed for smaller values (e.g., $\mathfrak{s}_1 \sim 0.1$). The lack of general proofs and the existence of counterexamples in specific string constructions are acknowledged.

The review also highlights the role of future observations (e.g., CMB, large-scale structure, gravitational waves) in testing the predictions of swampland-inspired models, particularly in constraining inflationary dynamics and the nature of dark energy.

---

Theoretical and Practical Implications

The swampland programme, as presented, has significant implications for both fundamental theory and phenomenology:

• Model Building: The conjectures provide sharp constraints on inflationary and dark energy models, favoring small-field, multi-field, or non-standard scenarios (e.g., warm inflation, rapid-turn dynamics).
• UV/IR Mixing: The emergence of light towers at large field distances links high-energy (UV) physics to low-energy (IR) observables, challenging the decoupling principle of EFT.
• Quantum Gravity Uniqueness: The cobordism conjecture and related arguments suggest a unique theory of quantum gravity, with all consistent backgrounds connected via domain walls.
• Observational Signatures: The conjectures motivate searches for light towers (e.g., axions, KK modes), deviations from $\Lambda$CDM, and signatures of extra dimensions or modified gravity.

---

Conclusion

The "Hitchhiker's Guide to the Swampland" provides a comprehensive and technically rigorous synthesis of the swampland programme and its cosmological ramifications. While many conjectures remain unproven and their applicability to the cosmological bulk is debated, the framework offers a powerful set of constraints and guiding principles for model building at the interface of quantum gravity and cosmology. The ongoing interplay between theoretical developments, string constructions, and observational data will be crucial in refining, falsifying, or substantiating the swampland conjectures. The review concludes with a call for continued dialogue between the string theory and cosmology communities, emphasizing the need for both theoretical innovation and empirical scrutiny.

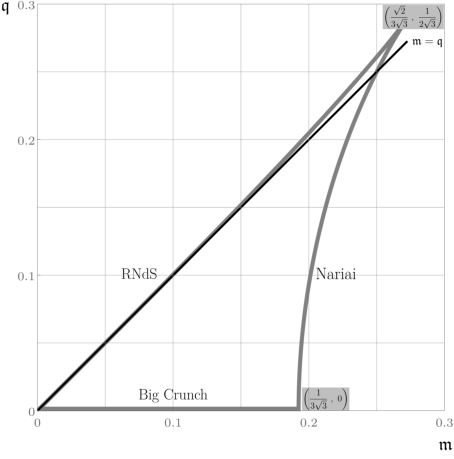
Figure 6: Phase space diagram of extremal black hole solutions in 4d Einstein-Maxwell-de Sitter, illustrating the interplay between different extremality branches and the implications for black hole evaporation and the cobordism conjecture.