RelP: Faithful and Efficient Circuit Discovery via Relevance Patching (2508.21258v1)

Abstract: Activation patching is a standard method in mechanistic interpretability for localizing the components of a model responsible for specific behaviors, but it is computationally expensive to apply at scale. Attribution patching offers a faster, gradient-based approximation, yet suffers from noise and reduced reliability in deep, highly non-linear networks. In this work, we introduce Relevance Patching (RelP), which replaces the local gradients in attribution patching with propagation coefficients derived from Layer-wise Relevance Propagation (LRP). LRP propagates the network's output backward through the layers, redistributing relevance to lower-level components according to local propagation rules that ensure properties such as relevance conservation or improved signal-to-noise ratio. Like attribution patching, RelP requires only two forward passes and one backward pass, maintaining computational efficiency while improving faithfulness. We validate RelP across a range of models and tasks, showing that it more accurately approximates activation patching than standard attribution patching, particularly when analyzing residual stream and MLP outputs in the Indirect Object Identification (IOI) task. For instance, for MLP outputs in GPT-2 Large, attribution patching achieves a Pearson correlation of 0.006, whereas RelP reaches 0.956, highlighting the improvement offered by RelP. Additionally, we compare the faithfulness of sparse feature circuits identified by RelP and Integrated Gradients (IG), showing that RelP achieves comparable faithfulness without the extra computational cost associated with IG.

• The paper introduces RelP, which replaces gradient terms with LRP-derived coefficients for efficient, faithful activation patching.
• RelP achieves higher Pearson correlation coefficients than AtP, notably reaching 0.956 in GPT-2 Large, underscoring its reliability.
• The technique scales across diverse transformer architectures and aids sparse feature circuit discovery, advancing mechanistic interpretability.

Faithful and Efficient Circuit Discovery via Relevance Patching

Introduction and Motivation

Mechanistic interpretability aims to localize and understand the internal components of neural networks responsible for specific behaviors. Activation patching, a causal intervention technique, is widely used for this purpose but is computationally prohibitive at scale. Attribution patching (AtP) offers a scalable, gradient-based approximation but suffers from noise and reduced reliability in deep, highly nonlinear models. The paper introduces Relevance Patching (RelP), which leverages Layer-wise Relevance Propagation (LRP) to replace local gradients in AtP with propagation coefficients, thereby improving faithfulness while maintaining computational efficiency.

Methodology: Relevance Patching (RelP)

RelP is designed to approximate the causal effects of activation patching with the computational efficiency of AtP. The key innovation is the substitution of the gradient term in AtP with the LRP-derived propagation coefficient. LRP propagates a relevance signal backward through the network using layer-specific rules that enforce properties such as relevance conservation and reduced noise. This approach is particularly effective in transformer architectures, where nonlinearities and normalization layers can disrupt the reliability of gradient-based attributions.

RelP requires only two forward passes and one backward pass, matching the efficiency of AtP. The propagation rules for transformer components—such as the LN-rule for LayerNorm, the Identity-rule for activation functions, and the AH-rule for attention—are critical for ensuring the faithfulness of the relevance signal. The method is model-agnostic in principle but requires careful rule selection for each architecture.

Empirical Evaluation: Indirect Object Identification (IOI) Task

The paper benchmarks RelP against AtP and activation patching (AP) on the IOI task across multiple model families and sizes, including GPT-2 (Small, Medium, Large), Pythia (70M, 410M), Qwen2 (0.5B, 7B), and Gemma2-2B. The evaluation metric is the Pearson correlation coefficient (PCC) between the results of each method and AP, computed over 100 IOI prompts.

RelP consistently achieves higher PCCs than AtP, especially in the residual stream and MLP outputs. For example, in GPT-2 Large, AtP yields a PCC of 0.006 for MLP outputs, while RelP achieves 0.956, indicating a substantial improvement in faithfulness.

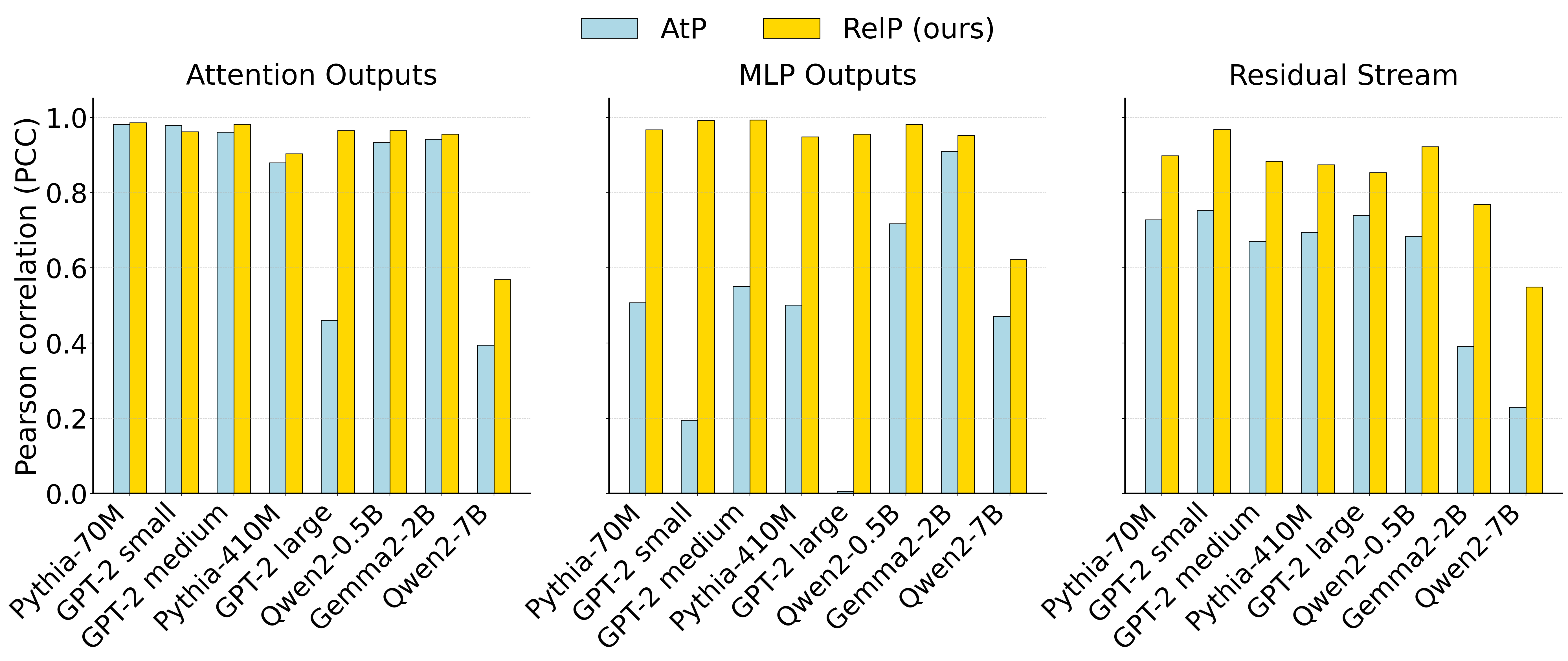
Figure 1: Pearson correlation coefficient (PCC) between activation patching and attribution patching (AtP) or relevance patching (RelP), computed over 100 IOI prompts for various model sizes and families.

Qualitative analyses further demonstrate that RelP aligns more closely with AP, particularly in components where AtP's linear approximation fails due to large activations or normalization-induced nonlinearity.

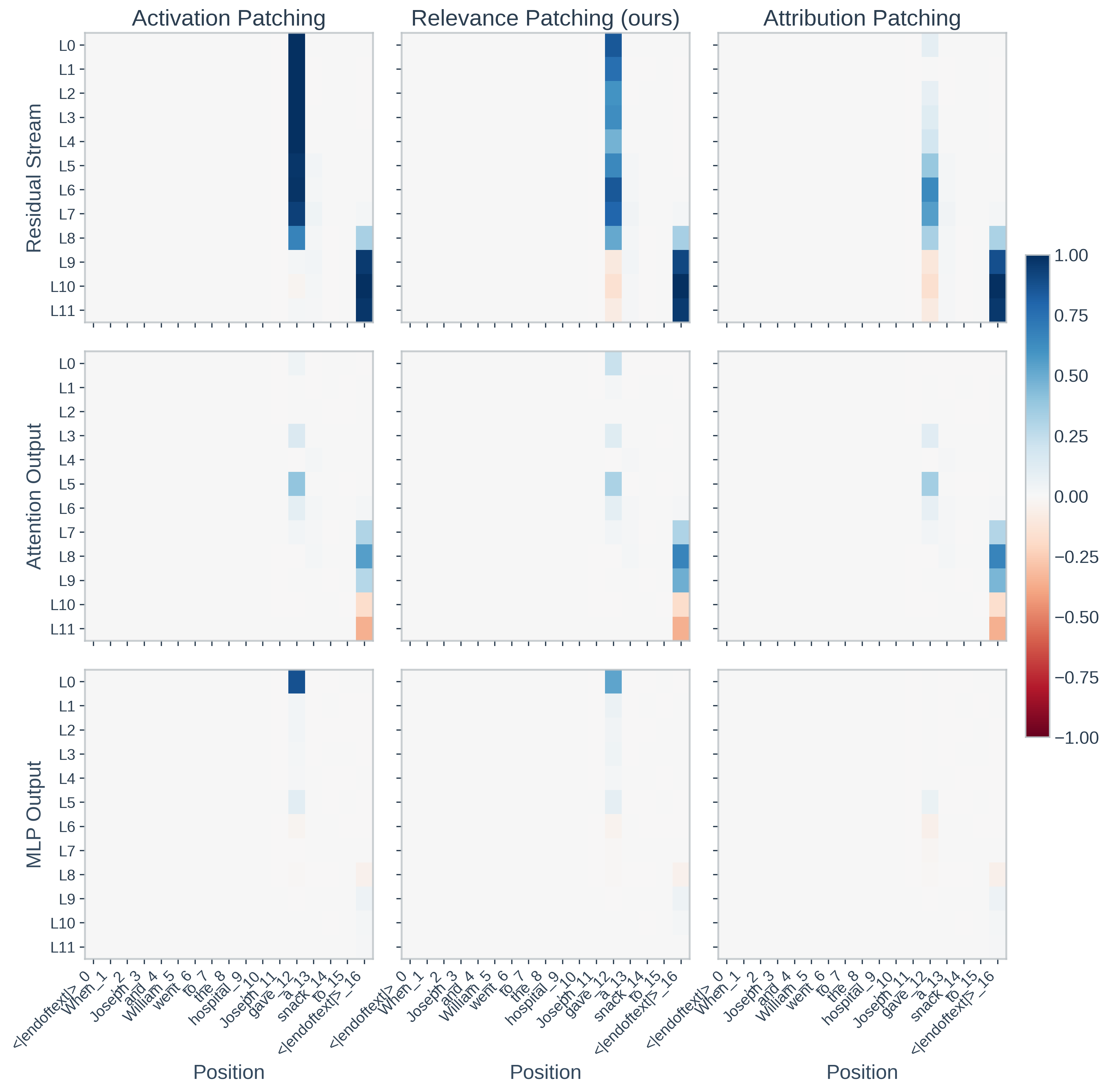
Figure 2: Qualitative comparison in GPT-2 Small showing RelP's superior alignment with activation patching in the residual stream and MLP0 compared to AtP.

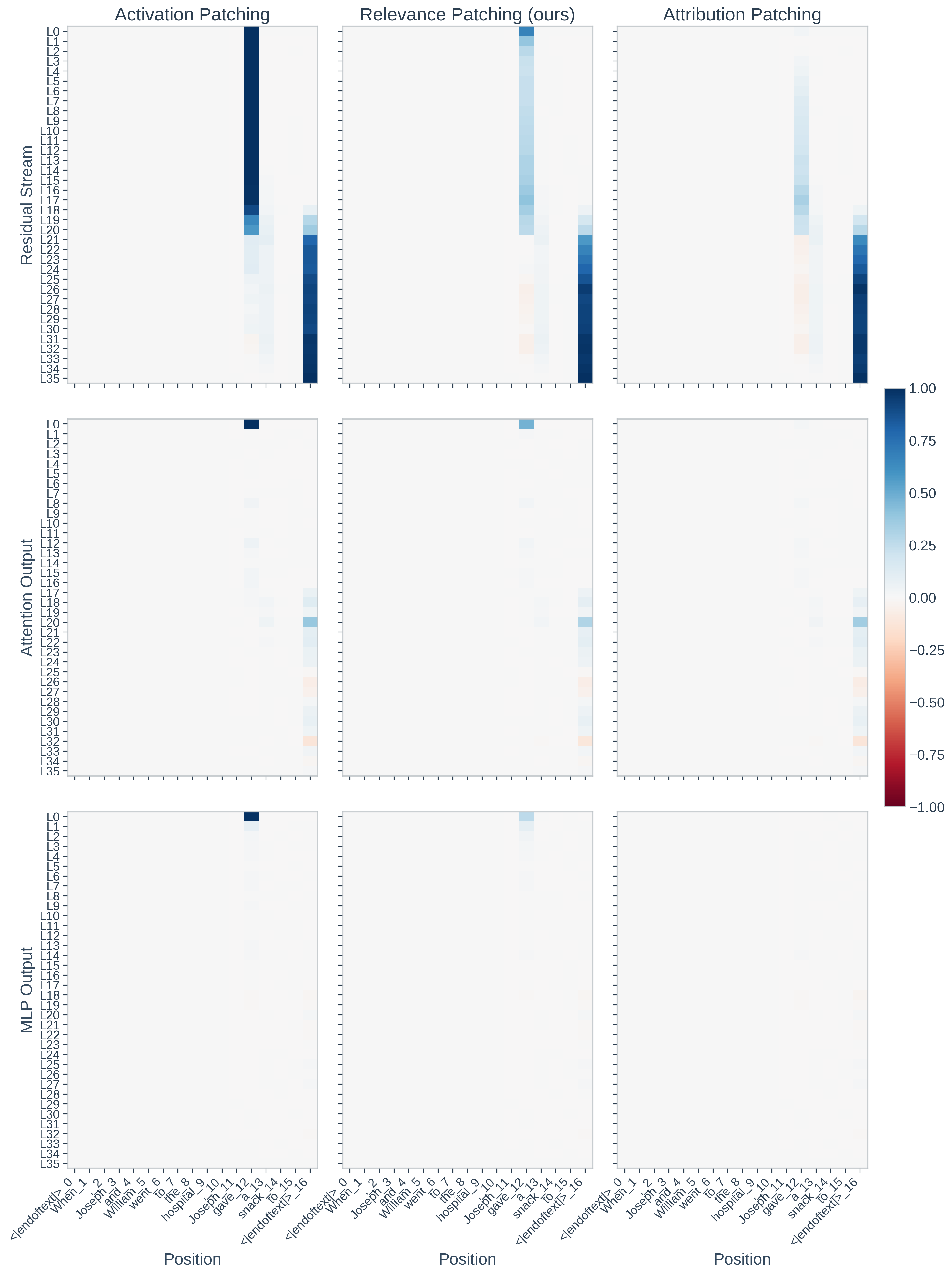
Figure 3: In GPT-2 Large, RelP maintains high fidelity to activation patching, especially in the residual stream and MLP0, where AtP's estimates are unreliable.

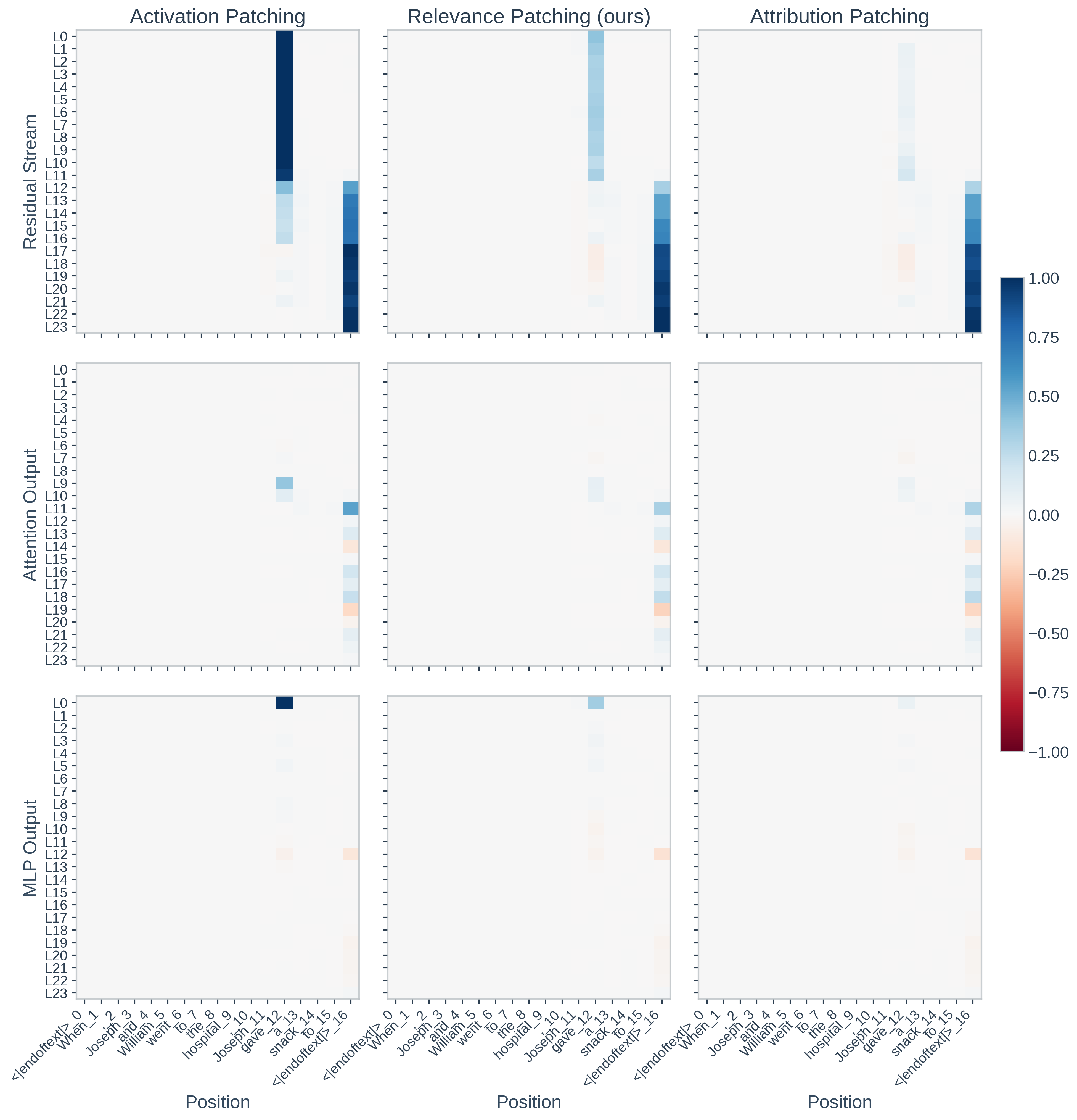
Figure 4: In Pythia-410M, RelP again demonstrates better alignment with activation patching than AtP, particularly in the residual stream and MLP0.

Sparse Feature Circuit Discovery

The paper extends RelP to the discovery of sparse feature circuits underlying subject-verb agreement in Pythia-70M, using features from sparse autoencoders (SAEs). Faithfulness and completeness metrics are used to evaluate the quality of the discovered circuits. RelP achieves faithfulness scores comparable to Integrated Gradients (IG) but with significantly lower computational cost, as IG requires multiple integration steps.

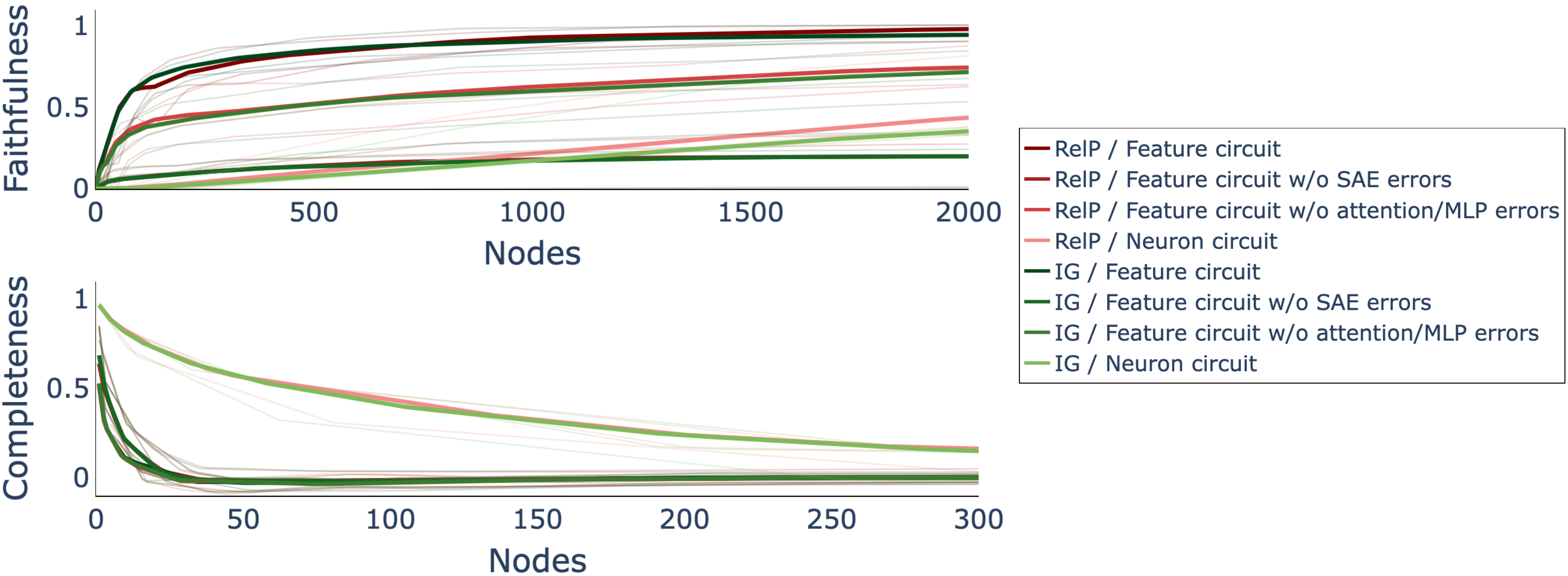
Figure 5: Faithfulness and completeness scores for circuits, showing that RelP matches IG in faithfulness without additional computational cost.

The analysis reveals that small feature circuits identified by RelP can explain most of the model's behavior, and ablating a few nodes from these circuits drastically reduces model performance. This efficiency is not matched by neuron circuits, which require orders of magnitude more components to achieve similar explanatory power.

Implementation Considerations

• Propagation Rule Selection: The effectiveness of RelP depends on the choice of LRP propagation rules for each model component. For transformers, specialized rules (LN-rule, Identity-rule, AH-rule, Half-rule) are necessary to maintain relevance conservation and reduce noise.
• Computational Efficiency: RelP matches AtP in computational cost (two forward passes, one backward pass), making it suitable for large-scale models and datasets.
• Scalability: The method is applicable to a wide range of transformer architectures and model sizes, as demonstrated empirically.
• Limitations: RelP requires model-specific rule selection, which introduces some overhead. Gains for attention outputs are less pronounced than for residual stream and MLP outputs, suggesting further refinement of propagation rules for self-attention may be beneficial.

Implications and Future Directions

RelP bridges the gap between the faithfulness of activation patching and the efficiency of gradient-based methods. Its integration of LRP into the patching framework enables more reliable circuit discovery in LLMs, facilitating mechanistic interpretability at scale. The approach is particularly valuable for tasks requiring the identification of sparse, causally relevant circuits, such as linguistic structure analysis and model editing.

Future work may focus on:

• Extending RelP to more complex behaviors and free-form text generation.
• Systematic studies of propagation rule selection for internal layers, especially in attention mechanisms.
• Application to closed-source or black-box models, where full access to internals is limited.
• Integration with automated circuit discovery pipelines and model compression techniques.

Conclusion

Relevance Patching (RelP) offers a principled and efficient method for faithful circuit discovery in neural LLMs. By leveraging LRP-derived propagation coefficients, RelP overcomes the limitations of gradient-based attribution patching, achieving high alignment with activation patching while maintaining scalability. The method demonstrates strong empirical performance across multiple architectures and tasks, and its integration into mechanistic interpretability workflows has the potential to advance both theoretical understanding and practical control of large-scale neural models.