Faster Linear Algebra Algorithms with Structured Random Matrices (2508.21189v1)

Abstract: To achieve the greatest possible speed, practitioners regularly implement randomized algorithms for low-rank approximation and least-squares regression with structured dimension reduction maps. Despite significant research effort, basic questions remain about the design and analysis of randomized linear algebra algorithms that employ structured random matrices. This paper develops a new perspective on structured dimension reduction, based on the oblivious subspace injection (OSI) property. The OSI property is a relatively weak assumption on a random matrix that holds when the matrix preserves the length of vectors on average and, with high probability, does not annihilate any vector in a low-dimensional subspace. With the OSI abstraction, the analysis of a randomized linear algebra algorithm factors into two parts: (i) proving that the algorithm works when implemented with an OSI; and (ii) proving that a given random matrix model has the OSI property. This paper develops both parts of the program. First, it analyzes standard randomized algorithms for low-rank approximation and least-squares regression under the OSI assumption. Second, it identifies many examples of OSIs, including random sparse matrices, randomized trigonometric transforms, and random matrices with tensor product structure. These theoretical results imply faster, near-optimal runtimes for several fundamental linear algebra tasks. The paper also provides guidance on implementation, along with empirical evidence that structured random matrices offer exemplary performance for a range of synthetic problems and contemporary scientific applications.

• The paper introduces the OSI property, a relaxation of OSE, enabling faster randomized linear algebra with structured, sparse sketching matrices.
• Empirical results demonstrate that constructions like SparseStack and SparseRTT achieve up to two orders of magnitude speedup with accuracy comparable to Gaussian sketches.
• Applications in scientific data compression and quantum partition function estimation validate the practical efficiency of the OSI-based algorithms.

Structured Random Matrices for Fast Randomized Linear Algebra

Introduction and Motivation

This paper develops a unified theoretical and practical framework for accelerating randomized linear algebra algorithms using structured random matrices. The central contribution is the introduction and systematic exploitation of the Oblivious Subspace Injection (OSI) property, a relaxation of the classical Oblivious Subspace Embedding (OSE) condition. The OSI abstraction enables the design and analysis of sketching algorithms that are both computationally efficient and empirically robust, even when the sketching matrices are highly structured (e.g., sparse, fast transform-based, or tensor-structured).

The authors demonstrate that many widely used randomized algorithms for low-rank approximation and least-squares regression can be implemented with OSIs, yielding near-optimal error guarantees and significant computational savings. The paper provides both theoretical analysis and extensive empirical evidence, including applications to scientific data compression and quantum partition function estimation.

The OSI Property: A New Abstraction

The OSI property is defined for a random matrix $\Phi \in F^{d \times k}$ (over $F = \mathbb{R}$ or $\mathbb{C}$) as follows:

• Isotropy: $\mathbb{E} \|\Phi^* x\|_2^2 = \|x\|_2^2$ for all $x \in F^d$.
• Injectivity: For any fixed $r$-dimensional subspace $V \subseteq F^d$, with high probability, $\|\Phi^* v\|_2^2 \geq \alpha \|v\|_2^2$ for all $v \in V$.

Unlike OSEs, OSIs do not require uniform control on the dilation (upper bound) of the embedding, only on the injectivity (lower bound). This relaxation is shown to be sufficient for the correctness of many randomized algorithms, and it allows for the use of much sparser or more structured sketching matrices.

Empirical Performance of Structured Sketches

The empirical paper demonstrates that structured random matrices (e.g., SparseStack, SparseRTT, Khatri–Rao) achieve approximation errors nearly indistinguishable from Gaussian sketches across a large and diverse testbed of real-world matrices.

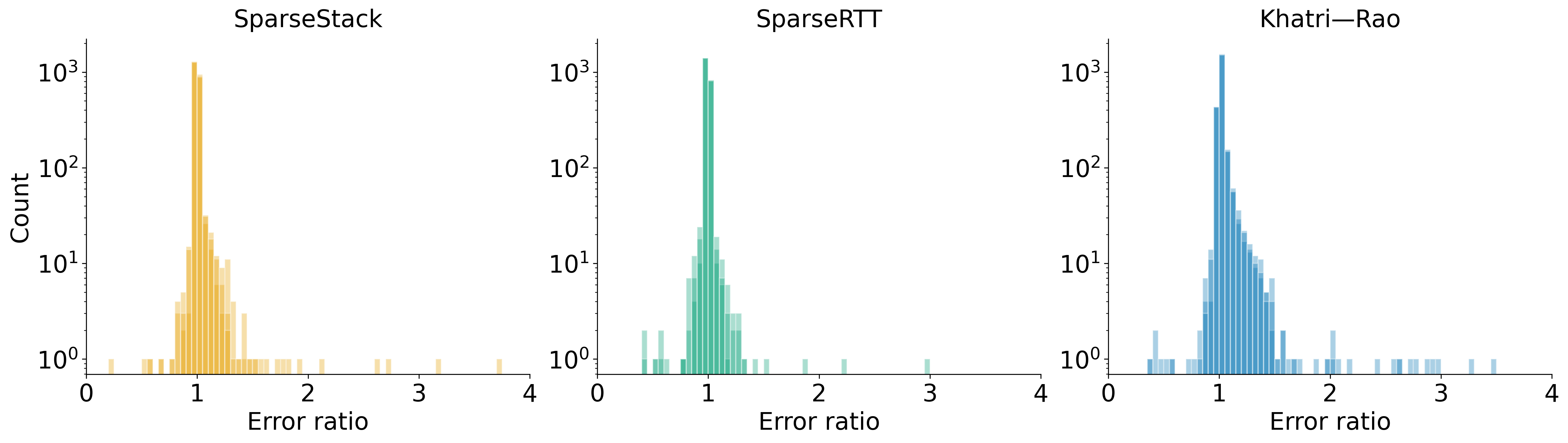
Figure 1: Histograms of the error ratio between structured and Gaussian sketches for randomized SVD on 2,314 SuiteSparse matrices; worst-case error ratio never exceeds 4, and structured sketches sometimes outperform Gaussians.

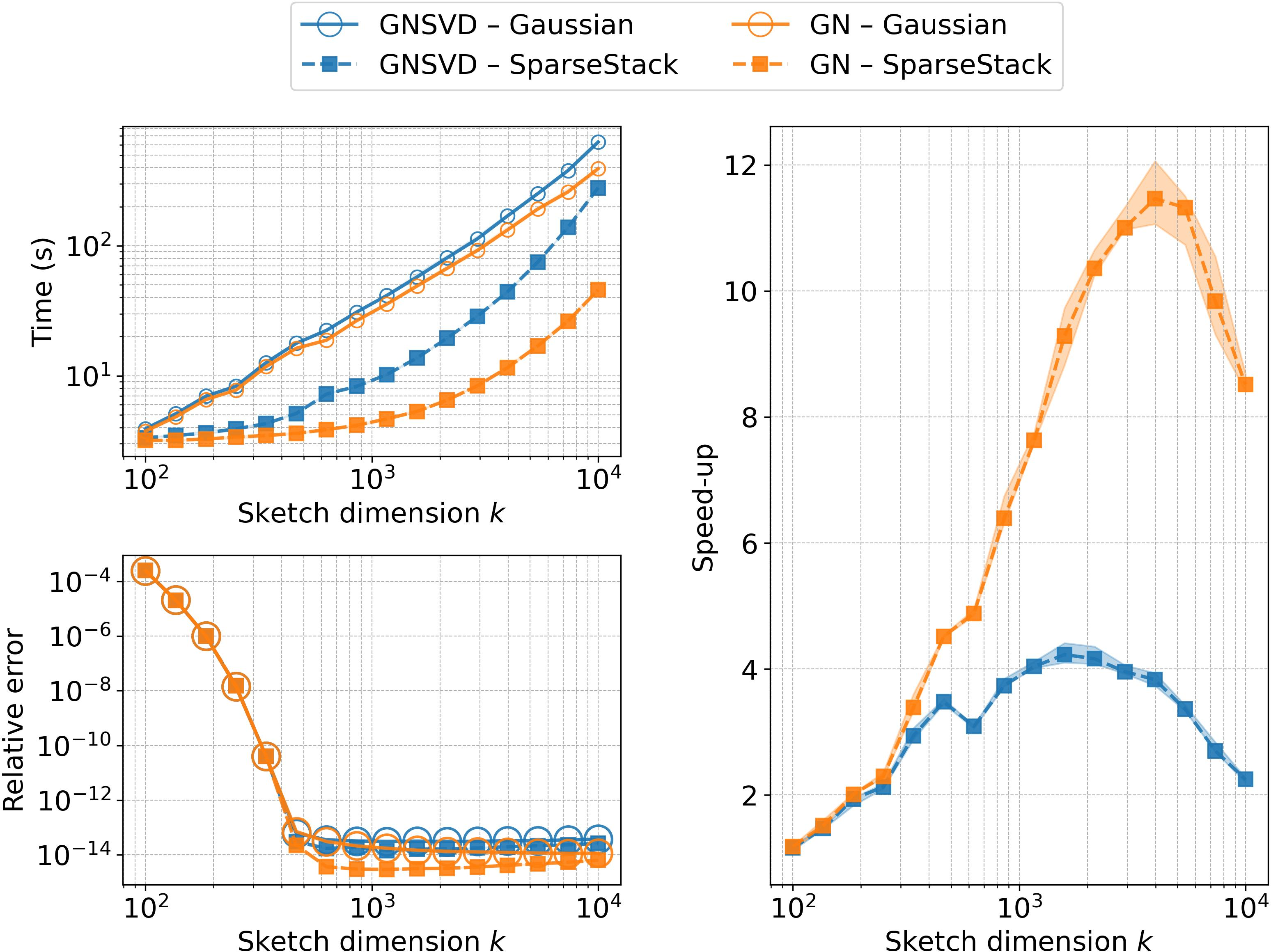
The computational advantage is substantial: for large matrices, sparse sketches can reduce the sketching time by up to two orders of magnitude compared to dense Gaussian sketches.

Sparse Sketching Matrices

Sparse random matrices, particularly the SparseStack construction, are analyzed in detail. The SparseStack is a concatenation of several CountSketch matrices, each with a small number of nonzeros per row. Theoretical results show that, for embedding dimension $k = O(r)$ and row sparsity $\zeta = O(\log r)$, SparseStack is an $(r, \alpha)$-OSI with constant $\alpha$. Empirically, even constant sparsity ($\zeta = 4$) suffices for robust performance.

Figure 2: Sparsity patterns for several sparse sketching matrices, illustrating the structural differences between SparseIID, SparseUniform, and SparseStack.

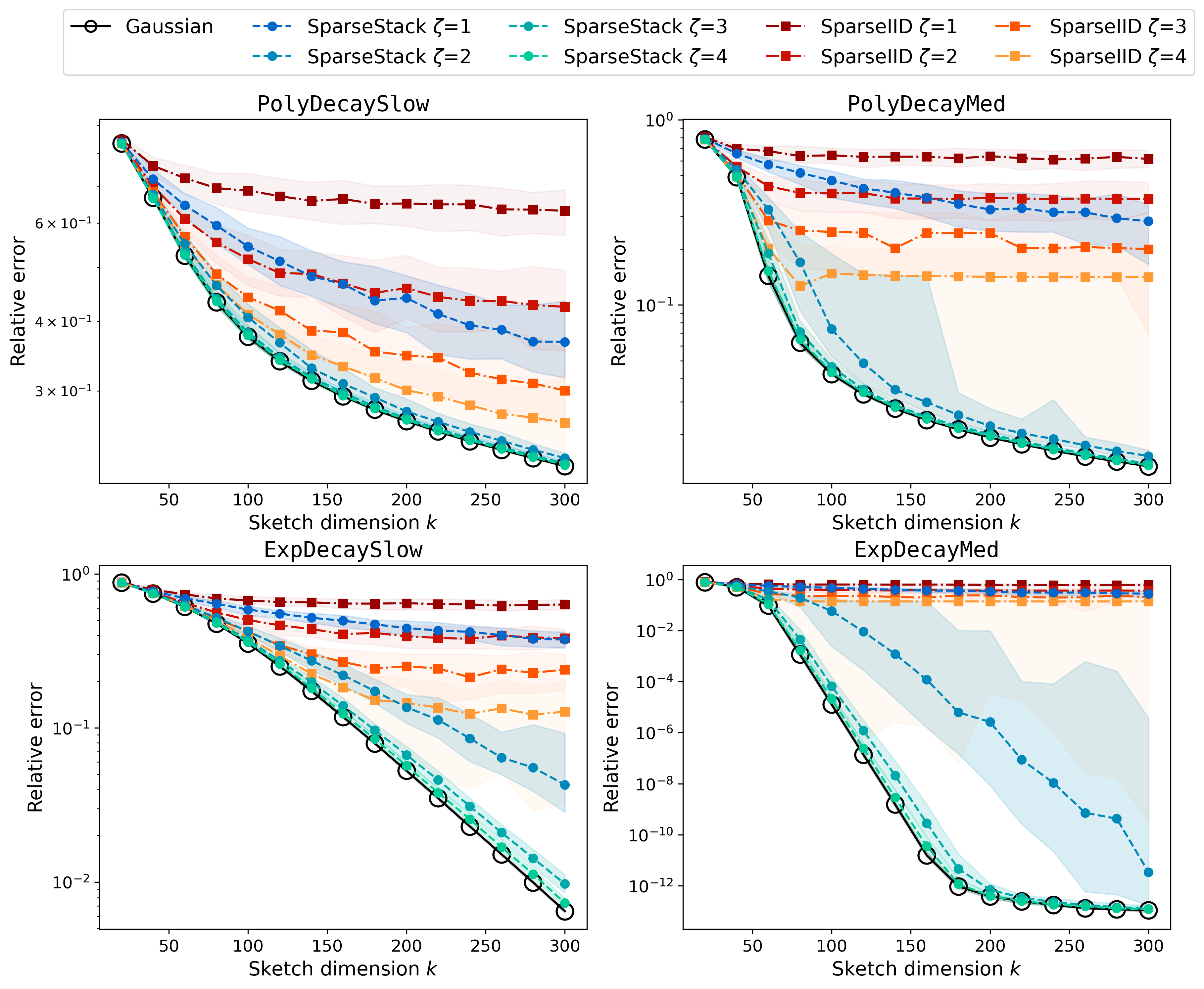
Figure 3: Relative error of RSVD using SparseStack and SparseIID sketches; SparseStack with $\zeta=4$ matches Gaussian accuracy, while SparseIID can fail for rapidly decaying spectra.

Fast Trigonometric Transform Sketches

The SparseRTT construction combines a random diagonal, a fast trigonometric transform (e.g., DCT, DFT, WHT), and a sparse sampling matrix. The authors show that, with column sparsity $\xi = O(\log r)$ and embedding dimension $k = O(r)$, SparseRTT achieves the OSI property and supports sketching in $O(nd \log r)$ time for an $n \times d$ input.

Figure 4: Relative error of RSVD using various fast trigonometric transform-based sketches; SparseCol sampling achieves superior accuracy at minimal sparsity.

Khatri–Rao and Tensor-Structured Sketches

For tensor-structured problems, the paper analyzes Khatri–Rao test matrices, where each column is a Kronecker product of independent random vectors. Theoretical results reveal an exponential dependence of the required embedding dimension on the tensor order $\ell$ for constant injectivity, but also show that for continuous base distributions, proportional embedding dimension is possible at the cost of exponentially small injectivity.

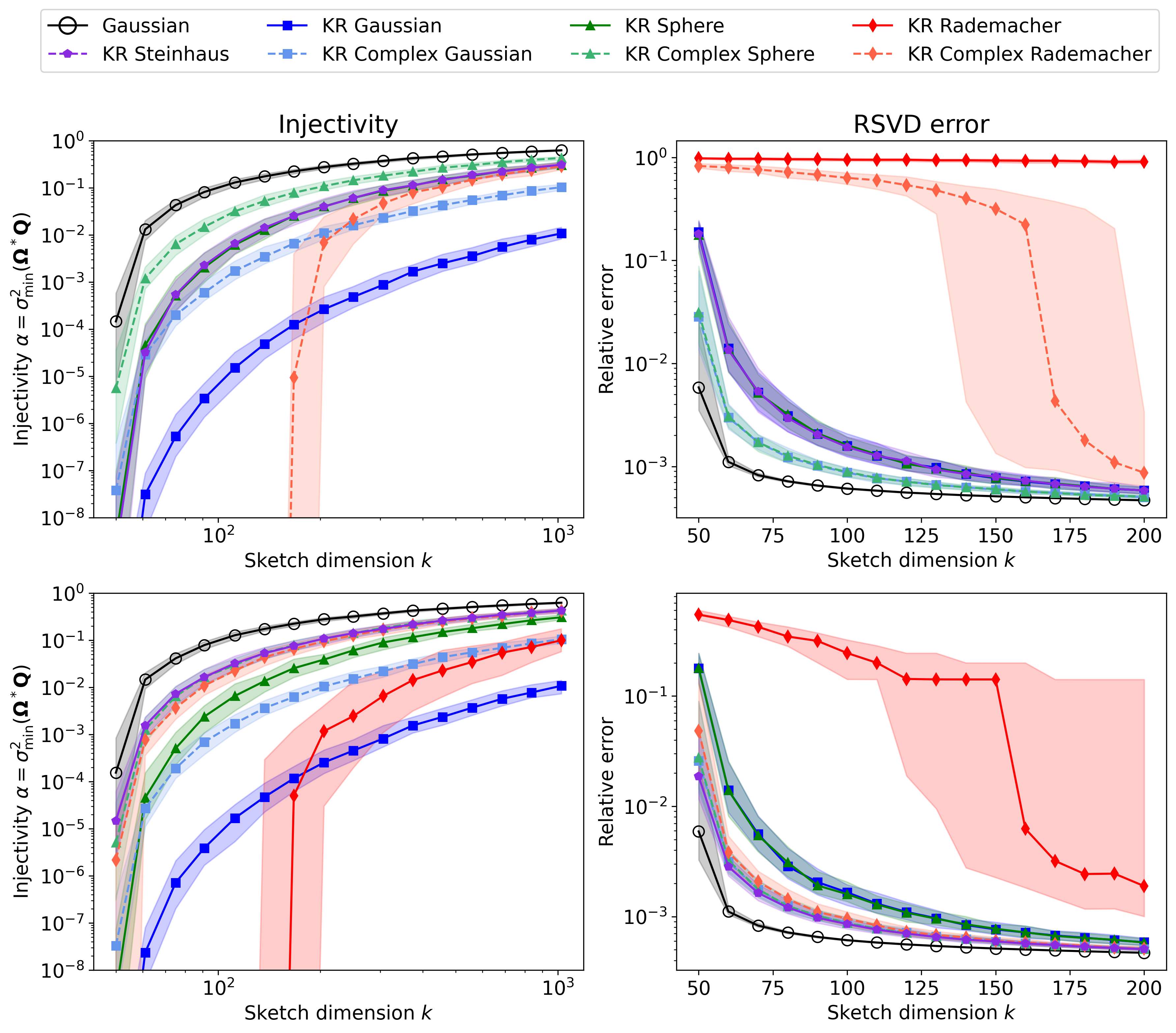
Figure 5: Injectivity and RSVD error for Khatri–Rao sketches with various base distributions; real Rademacher fails catastrophically, while complex spherical and Steinhaus distributions are robust.

Scientific Applications

The practical impact of these methods is demonstrated in two scientific domains:

• Scientific Data Compression: Using SparseStack with generalized Nyström SVD, the authors achieve up to $12\times$ speedup over Gaussian sketches for compressing large-scale simulation data, with no loss in accuracy.

  Figure 6: Relative error and runtime for scientific data compression using SparseStack versus Gaussian sketches; SparseStack achieves substantial speedup with comparable accuracy.

• Quantum Partition Function Estimation: Khatri–Rao sketches enable variance-reduced trace estimation for quantum systems with large tensor order, achieving up to 12 digits of precision where baseline methods fail.

Theoretical Techniques for OSI Analysis

The paper develops and applies several probabilistic tools for establishing the OSI property:

• Fourth-Moment Bounds: Used for Khatri–Rao sketches with constant injectivity.
• Small-Ball Probabilities: Enable proportional embedding dimension for continuous base distributions.
• Gaussian Comparison: Provides sharp lower bounds for the minimum singular value of sparse sketching matrices.
• Matrix Concentration: Used for classical OSE analysis, but shown to be suboptimal for OSI.

Implications and Future Directions

The OSI framework unifies the analysis of a broad class of structured random matrices, enabling the design of faster and more resource-efficient randomized linear algebra algorithms. The empirical and theoretical results challenge the prevailing view that only OSEs (and thus, typically, dense Gaussian sketches) are suitable for high-quality randomized algorithms. The evidence supports the deployment of highly sparse and structured sketches in large-scale scientific and machine learning applications.

Notably, the paper provides strong numerical evidence and theoretical justification that constant-factor error guarantees are sufficient for most practical applications, and that the OSI property is both necessary and sufficient for many randomized algorithms. This opens the door to further research on even more efficient sketching constructions, as well as the extension of the OSI framework to other algorithmic domains.

Conclusion

This work establishes the OSI property as a central abstraction for the design and analysis of fast randomized linear algebra algorithms with structured random matrices. By decoupling the requirements for injectivity and dilation, the authors enable the use of highly efficient sketching matrices without sacrificing output quality. The theoretical framework is complemented by extensive empirical validation and practical guidance, making the results immediately applicable to large-scale scientific and data-driven computing. Future research may focus on extending OSI-based analysis to broader classes of algorithms and exploring the limits of sparsity and structure in randomized numerical linear algebra.