TASI lectures on Matrix Theory from a modern viewpoint (2508.20970v1)

Abstract: These notes review the D0-brane or Banks-Fischler-Shenker-Susskind (BFSS) matrix quantum mechanics from a post-AdS/CFT perspective. We start from the decoupling argument for D0-branes and discuss the gravity dual in the 't Hooft regime, before extrapolating to strong coupling. In the second part of these notes, we review the matrix bootstrap method and its application to the D0-brane quantum mechanics.

• The paper explores the BFSS matrix model as a non-perturbative definition of M-theory by analyzing D0-brane holography and operator scaling.
• It applies novel matrix bootstrap methods alongside Monte Carlo simulations to bound observables and clarify black hole dynamics.
• The study bridges analytic and numerical techniques, providing insights into gauge/gravity duality and emergent spacetime structures.

TASI Lectures on Matrix Theory from a Modern Viewpoint

Overview and Motivation

This work provides a comprehensive review of the BFSS matrix quantum mechanics, focusing on its role as a non-perturbative definition of M-theory and its connections to gauge/gravity duality. The lectures are organized into two main parts: the first revisits D0-brane holography and the gravity dual from a post-AdS/CFT perspective, while the second surveys modern numerical and analytic approaches to matrix models, with an emphasis on the matrix bootstrap method.

The BFSS model is distinguished by its simplicity—being a quantum mechanical system rather than a field theory—yet it encapsulates the emergence of spacetime and black hole dynamics. The review leverages advances in gauge/gravity duality and computational techniques to clarify the physical content and computational challenges of the model.

D0-Brane Holography and Decoupling Limit

The gravity dual of the BFSS model is constructed from the near-extremal D0-brane black hole solution in Type IIA supergravity. The decoupling limit isolates the low-energy dynamics of the D0-branes, leading to a factorization of the Hilbert space into flat space and near-horizon sectors. The latter is identified with the Hilbert space of maximally supersymmetric SU($N$) quantum mechanics.

The geometry in the decoupling limit exhibits a throat region whose size and thermodynamic properties are controlled by the 't Hooft coupling and temperature. The effective string coupling remains finite, necessitating the large $N$ limit for a reliable semiclassical description. The analysis also generalizes to other D$p$-brane systems, with distinct IR behaviors and dualities.

(Figure 1)

Figure 1: Penrose diagram illustrating the decoupling of the near-horizon region for D0-brane black holes, with the emergence of a throat geometry analogous to AdS black branes.

Operator Dictionary and Scaling Dimensions

The lectures derive the "differentiate dictionary" for operator correspondence, showing that deformations of the SYM Lagrangian map to boundary conditions for supergravity modes in the throat. The spectrum of operators, particularly BPS operators of the form $\Tr X^{(I_1} \cdots X^{I_k)}$, is analyzed using group theory and supersymmetry. Their scaling dimensions are computed via the effective AdS$_{d+1}$ description, yielding $\Delta = \frac{2}{5} k$ for the BFSS case.

A scaling symmetry of the gravity solution underlies the temperature dependence of thermodynamic quantities and the power-law behavior of correlation functions for protected operators.

Black Hole Thermodynamics and Monte Carlo Studies

The thermodynamics of the D0-brane black hole is governed by a double expansion in temperature and $1/N$, with analytic control over leading coefficients and exponents. Higher-order corrections involve unknown stringy and M-theory terms, but Monte Carlo simulations have provided numerical estimates for subleading coefficients, including evidence for 11d M-theory physics.

Matrix Quantum Mechanics: Spectrum and Scattering

The BFSS matrix model consists of 9 bosonic and 16 fermionic Hermitian traceless matrices, with a unique normalizable zero-energy ground state and a continuum of scattering states. The structure of the wavefunction exhibits power-law tails associated with block-diagonal configurations, reflecting the multi-center nature of the gravity dual.

Scattering amplitudes in the matrix model are matched to multi-center black hole solutions in supergravity, with the effective action for slow-moving D0-branes reproducing the expected velocity-dependent potentials. Supersymmetry ensures non-renormalization of certain terms, enabling extrapolation from weak to strong coupling.

The BFSS conjecture posits that the matrix model computes the M-theory S-matrix in the infinite $N$ limit, with precise matching of polarization states and kinematics. The ultra-strong coupling regime probes 11d black hole dynamics, and the conjecture is supported by both analytic and numerical evidence.

Analytic and Numerical Techniques

High-Temperature and Weak Coupling Expansions

Perturbative expansions are feasible in the high-temperature or large-mass limits, with non-trivial matrix integrals remaining at leading order.

Supersymmetric Localization and Index Computations

Supersymmetric techniques, including localization and index computations, provide exact results for protected quantities in mass-deformed models (BMN, IKKT), but are limited in the massless BFSS case due to SO(9) symmetry.

Matrix Bootstrap

The matrix bootstrap is a non-perturbative, large $N$ approach that leverages Schwinger-Dyson equations and positivity constraints to bound observables. For single and multi-matrix models, the method yields rigorous inequalities and, in favorable cases, convergent islands for correlation functions.

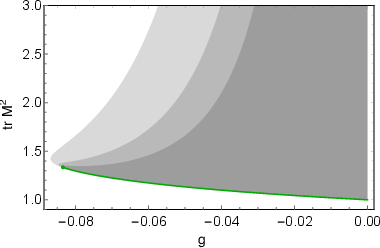
Figure 2: 1-matrix model bootstrap for unbounded potential $$V = \frac12 \mathrm{tr} M^2 + \frac{g}{4} \mathrm{tr} M^4$$, showing rapid convergence of the allowed region to the critical value of $g$.

The quantum mechanical bootstrap generalizes these ideas to time-dependent and thermal ensembles, incorporating energy-entropy balance inequalities and ground state positivity. The method is robust to sign problems and metastability, making it suitable for strongly coupled systems.

Application to BFSS and Bosonic Matrix Models

Bootstrap bounds have been applied to the BFSS ground state, yielding analytic and numerical estimates for the size of the bound state wavefunction. The results confirm that $r/\ell_p \gtrsim N^{1/3}$, consistent with the supergravity region and in close agreement with Monte Carlo simulations.

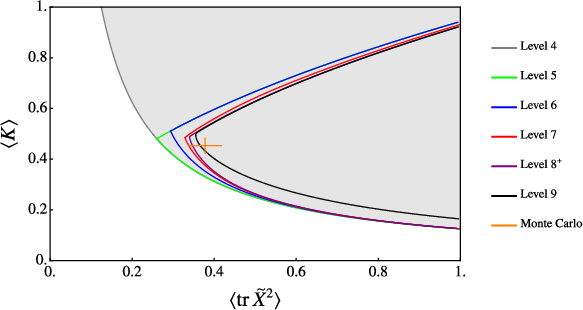
Figure 3: Bootstrap bounds for the BFSS ground state, with the allowed region converging toward the Monte Carlo result for the kinetic energy in 't Hooft units.

For the massless $D=9$ bosonic Yang-Mills matrix model, bootstrap islands have been found at high levels, with rapid convergence to the Monte Carlo and $1/D$ expansion results.

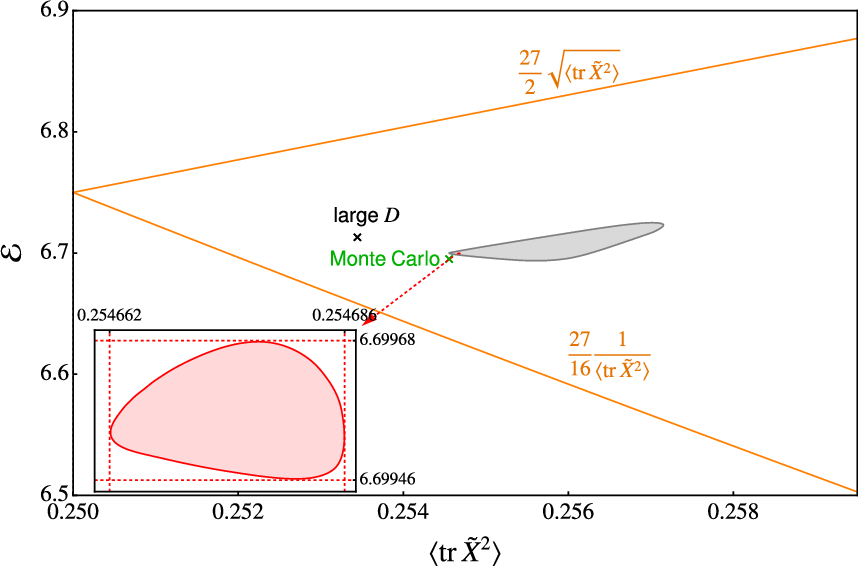
Figure 4: Bootstrap bounds for the massless $D=9$ bosonic Yang-Mills matrix model ("bosonic BFSS"), showing the emergence and shrinkage of the allowed island at increasing levels.

Implications and Future Directions

The BFSS matrix model remains a central tool for probing non-perturbative aspects of M-theory, black hole microphysics, and the emergence of spacetime. The matrix bootstrap and related techniques offer promising avenues for rigorous bounds and potentially precise computations of unprotected quantities. The interplay between analytic, numerical, and group-theoretic methods is crucial for advancing our understanding of strongly coupled quantum systems.

Future work should focus on extending bootstrap methods to higher levels, exploring time-dependent and thermal properties, and comparing results across different approaches (Monte Carlo, AdS/CFT flat space limits, S-matrix bootstrap). The ultimate goal is to achieve a detailed, quantitative understanding of M-theory amplitudes and black hole dynamics from first principles.

Conclusion

This review synthesizes modern perspectives on matrix theory, emphasizing the utility of the BFSS model as a non-perturbative definition of M-theory and a laboratory for quantum gravity. Advances in computational and analytic techniques, particularly the matrix bootstrap, have enabled significant progress in bounding and estimating physical observables. Continued development of these methods is likely to yield deeper insights into the structure of quantum gravity and holography in flat space.