Optimal Work Extraction from Finite-Time Closed Quantum Dynamics (2508.20512v1)

Abstract: Extracting useful work from quantum systems is a fundamental problem in quantum thermodynamics. In scenarios where rapid protocols are desired -- whether due to practical constraints or deliberate design choices -- a fundamental trade-off between power and efficiency emerges as a key concern. Here, we investigate the problem of finite-time optimal work extraction from closed quantum systems, subject to a constraint on the magnitude of the control Hamiltonian. We first establish the trade-off relation between power and work under a general setup, stating that these fundamental performance metrics cannot be maximized simultaneously. Next, we introduce a framework of Lie-algebraic control, which involves a wide range of control problems including many-body control of the Heisenberg model and the SU(n)-Hubbard model. Within this framework, the optimal work extraction protocol becomes remarkably simple: it suffices to use a time-independent Hamiltonian, which is determined by a nonlinear self-consistent equation. We obtain an analytical solution for su(2) control, and a numerical solution for more complex cases like su(n) control using the steepest gradient descent method. Moreover, by exploiting the Lie-algebraic structure of the controllable terms, our approach is applicable to quantum many-body systems, enabling an efficient numerical computation. Our results highlight the necessity of rapid protocols to achieve the maximum power and establish a theoretical framework for designing optimal work extraction protocols under realistic time constraints.

• The paper establishes that maximal power is reached strictly before maximal work extraction, highlighting a trade-off under norm constraints.
• It introduces a Lie-algebraic control framework with simple, efficient protocols, offering analytical solutions for su(2) systems and numerical methods for higher dimensions.
• The framework extends to many-body systems and general expectation value optimization, impacting rapid quantum battery charging, cooling, and state preparation.

Optimal Work Extraction from Finite-Time Closed Quantum Dynamics

Introduction and Motivation

This paper addresses the problem of extracting maximal work from closed quantum systems within finite operational time, under realistic constraints on the control Hamiltonian's magnitude. The paper is motivated by practical limitations in experimental quantum thermodynamics, such as decoherence, system stability, and bounded control resources, which necessitate rapid protocols. The work extraction problem is formalized in terms of maximizing the energy reduction (or equivalently, cooling) of a quantum system, given initial and final Hamiltonians, an initial state, and a time-dependent control Hamiltonian subject to a norm constraint.

Trade-Off Between Power and Work

A central result is the rigorous establishment of a trade-off between power and extractable work. The paper proves that the maximum power (work per unit time) is achieved strictly before the time required for maximal work extraction. This no-go theorem implies that protocols maximizing work and those maximizing power are fundamentally distinct; rapid protocols are necessary to achieve high power, even at the expense of total extractable work. The differentiability of the optimal work function at its maximum is shown, and the derivative of power at this point is strictly negative, confirming the trade-off.

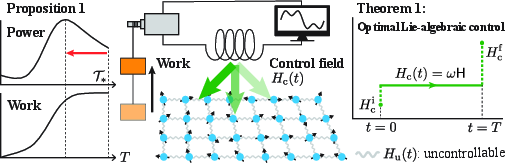
Figure 1: Schematic of finite-time work extraction, illustrating the decomposition of the Hamiltonian into controllable and uncontrollable parts, and the trade-off between power and work under norm constraints.

Lie-Algebraic Control Framework

To address the complexity of time-dependent optimal control, the paper introduces a Lie-algebraic control framework. The controllable part of the Hamiltonian is restricted to a Lie algebra $\mathcal{V}$, closed under commutation, while the uncontrollable part commutes with all elements of $\mathcal{V}$. This structure encompasses physically relevant models, such as Heisenberg spin systems with global magnetic field control and $\mathrm{SU}(n)$-Hubbard models with flavor control.

Within this framework, the optimal protocol is shown to be remarkably simple: the system is driven by a time-independent control Hamiltonian, determined by a nonlinear self-consistent equation. The protocol consists of three steps: (i) quenching to the optimal control Hamiltonian, (ii) evolution under this time-independent Hamiltonian, and (iii) quenching to the final Hamiltonian.

Analytical Solution for $\mathfrak{su}(2)$ Control

For $\mathfrak{su}(2)$ control (e.g., two-level systems or Heisenberg models with global field control), the self-consistent equation admits an analytical solution. The optimal control Hamiltonian is aligned with the commutator of the final Hamiltonian and the initial state's projection onto the controllable subspace. The extractable work exhibits a cosine dependence on the operational time $T$, with the minimum time for maximal work extraction given by the angle between the initial state and final Hamiltonian in operator space.

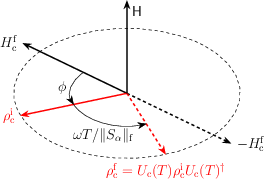
Figure 2: Optimal work-extraction protocol under $\mathfrak{su}(2)$ control, showing the geometric rotation of the projected density operator on the Bloch sphere.

Numerical Solution for Higher-Dimensional Control Algebras

For higher-dimensional Lie algebras (e.g., $\mathfrak{su}(n)$ with $n>2$), the self-consistent equation is solved numerically using a gradient-based method. The cost function quantifies the deviation from the self-consistent equation, and its gradient is computed analytically. The method is significantly more efficient than direct optimization over time-dependent protocols.

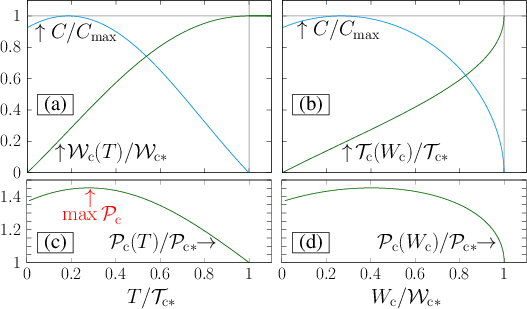
Figure 3: Optimal work extraction from a random three-level system under full $\mathfrak{su}(3)$ control, showing the dependence of extractable work, minimum time, and power on operational time.

Efficient Computation for Many-Body Systems

A key technical contribution is the demonstration that, for many-body systems with Lie-algebraic control, the optimization can be performed in a reduced representation whose dimension is independent of system size. For example, in $\mathrm{SU}(n)$-Hubbard models, the relevant operations are performed in the $n$-dimensional standard representation, enabling efficient computation even for exponentially large Hilbert spaces. The reduction leverages the orthogonal decomposition of the control algebra and the invariance of the Hilbert-Schmidt inner product under representation.

Extension to General Expectation Value Optimization

The framework generalizes beyond work extraction to the optimization of arbitrary expectation values at the final time, provided the control algebra spans all Hermitian or all traceless Hermitian operators. This includes tasks such as fidelity maximization with respect to a target state. The self-consistent equation is modified accordingly, and analytical solutions are available for two-level systems, while numerical methods apply for higher dimensions.

Implications and Future Directions

The results provide a rigorous and computationally tractable framework for finite-time optimal control in closed quantum systems, with direct applications to quantum batteries, cooling, and state preparation. The identification of a broad class of systems amenable to Lie-algebraic control, and the reduction of computational complexity for many-body systems, are significant for both theoretical and experimental quantum thermodynamics.

Theoretical implications include the exact characterization of quantum speed limits for work extraction, in contrast to previous unattainable bounds. Practically, the framework enables the design of rapid protocols that balance power and efficiency under realistic constraints.

Future research directions include extending the framework to cases where Lie-algebraic control assumptions are relaxed, exploring generalizations to many-body systems with full control, and synthesizing known results in the finite-time regime for various target operators.

Conclusion

This paper establishes a general theory for optimal work extraction from closed quantum systems under finite-time and norm constraints, rigorously characterizing the trade-off between power and work. The Lie-algebraic control framework yields simple and efficient protocols, with analytical and numerical solutions applicable to both few-level and many-body systems. The approach generalizes to the optimization of arbitrary observables, providing a versatile tool for quantum control and thermodynamics. The reduction in computational complexity for many-body systems and the exact quantum speed limits are particularly notable, with broad implications for experimental and theoretical advances in quantum technologies.