Using Symbolic Regression to Emulate the Radial Fourier Transform of the Sérsic profile for Fast, Accurate and Differentiable Galaxy Profile Fitting (2508.20266v1)

Abstract: Galaxy profile fitting is a ubiquitous technique that provides the backbone for photometric and morphological measurements in modern extragalactic surveys. A recent innovation in profile fitting algorithms is to render, or create, the model profile in Fourier space, which aims to provide faster and more accurate results. However, the most common parameterization, the S\'ersic profile, has no closed form Fourier transform, requiring the use of computationally expensive approximations. In this paper our goal is to develop an emulator to mimic the radial Fourier transform of the S\'ersic profile, for use in profile fitting. We first numerically compute the radial Fourier transform and demonstrate that it varies smoothly as a function of the S\'ersic index and $k$, the spatial frequency coordinate. Using this set of numerically calculated transforms as a training set, we use symbolic regression to discover an equation which approximates its behavior. This ensures the emulator will be based on computationally efficient and differentiable building blocks. We implement this novel rendering method in the pysersic profile fitter, and ensure it is accurate by conducting both injection-recovery tests using model galaxy profiles and applying multiple rendering methods to a real sample of galaxies in HSC-SSP imaging. Crucially, the Fourier emulator rendering technique enables measurements of morphological parameters of galaxies 2.5 times faster than standard methods with minimal loss in accuracy. This increased performance while maintaining accuracy is a step that ensures these tools can continue to scale with the ever-increasing flow of incoming data.

• The paper introduces a novel symbolic regression-based emulator to approximate the radial Fourier transform of the Sérsic profile for efficient galaxy fitting.
• It validates the method via injection-recovery tests and real galaxy data, achieving less than 0.5% bias and low scatter in recovered parameters.
• The approach enables a 2.5× speedup in inference time while balancing equation complexity and computational efficiency.

Symbolic Regression for Emulating the Radial Fourier Transform of the Sérsic Profile in Galaxy Fitting

Introduction

The Sérsic (S) profile is the canonical parametric model for describing the surface brightness distribution of galaxies, parameterized by total flux, effective radius, and the Sérsic index $n$. Accurate and efficient fitting of these profiles to imaging data is foundational for extragalactic astronomy, underpinning photometric and morphological measurements in large surveys. However, the lack of a closed-form Fourier transform for the S profile complicates fast and differentiable rendering, especially for gradient-based inference and large-scale data processing. This paper introduces a symbolic regression-based emulator for the radial Fourier (Hankel) transform of the S profile, enabling fast, accurate, and differentiable galaxy profile fitting.

Numerical Characterization of the Radial Fourier Transform

The radially symmetric Fourier transform of the S profile, essential for Fourier-space rendering, is given by:

$$\mathcal{F}_r(k) = 2\pi\int_0^\infty I(R) J_0(kR)R\, dR$$

where $J_0$ is the zeroth-order Bessel function. The authors numerically compute this transform using the hankel Python package, sampling a range of $n$ and $k$ values. The resulting transforms are smooth, bounded between 0 and 1, and exhibit well-defined asymptotic behavior: approaching 1 as $k\to0$ and 0 as $k\to\infty$. The variation with $n$ is also smooth, suggesting the feasibility of emulation.

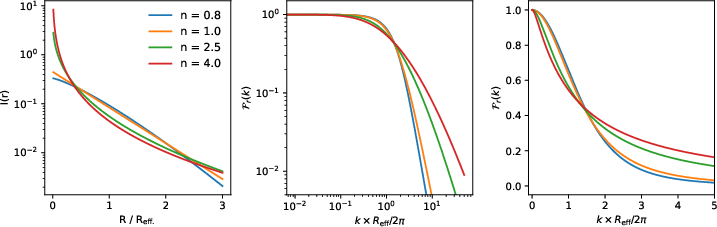
Figure 1: The S profile and its radial Fourier (Hankel) transform for several $n$ values, showing smooth, bounded behavior suitable for emulation.

Symbolic Regression-Based Emulation

Fitting Procedure

The core innovation is the use of symbolic regression (via the pysr package) to discover an analytical approximation to the numerically computed $\mathcal{F}_r(k, n)$. The search is constrained to functions of the form:

$$\tilde{\mathcal{F}_r}(k, n) = \frac{1}{1 + e^{G(k, n)}}$$

where $G(k, n)$ is a symbolic expression evolved to minimize L2 loss against the numerical transform. The training set consists of 10,000 $(k, n)$ pairs, with $n$ sampled uniformly in $[0.4, 6.5]$ and $k$ exponentially distributed to match typical Fourier grids. The symbolic regression is run for $2.5 \times 10^6$ iterations, with operator constraints to ensure numerical stability and differentiability.

Equation Selection and Trade-offs

A key result is the empirical observation of a trade-off between equation complexity and computational efficiency: more complex expressions yield higher accuracy but incur greater computational cost. Above a complexity threshold ($\sim$30), accuracy plateaus while execution time continues to increase. The selected emulator equation (complexity 39) achieves L2 loss $<2 \times 10^{-6}$ and is computationally efficient, with minimal nested expensive operations in $k$.

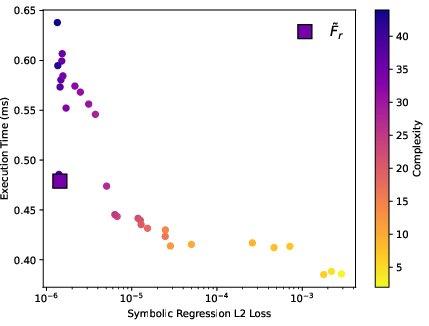
Figure 2: Trade-off between execution time and accuracy for candidate symbolic regression equations; the selected emulator lies at the optimal efficiency-accuracy frontier.

The explicit form of the emulator is:

$$\tilde{\mathcal{F}_r}(k, n) = \frac{1}{1 + \exp\left(\frac{1}{n} \left( [H(k, n) + J(k, n)] (\log k - a_4) - a_5 \right)\right)}$$

with $H$ and $J$ as defined in the paper, and constants $a_i$ empirically determined.

Validation: Injection-Recovery and Real Data

Injection-Recovery Tests

The emulator is implemented in the pysersic codebase and validated via injection-recovery tests. Synthetic S profiles are rendered with a highly oversampled pixel-space renderer and then fit using the emulator-based Fourier renderer. The recovered effective radii and Sérsic indices agree with the true values to within $<0.5\%$ bias and $<2\%$ scatter, demonstrating negligible loss in accuracy.

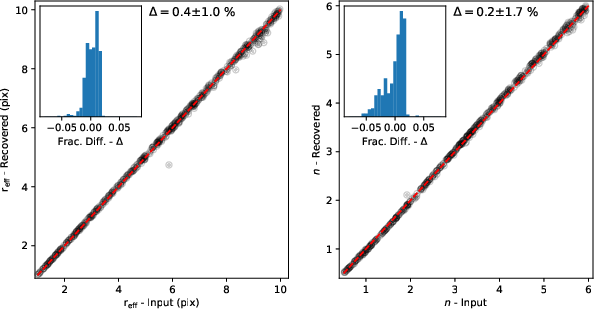
Figure 3: Injection-recovery tests show the emulator-based renderer recovers $r_{\rm eff}$ and $n$ with $<0.5\%$ bias and $<2\%$ scatter.

Application to HSC-SSP Galaxy Imaging

The emulator is further tested on 100 galaxies from the GAMA survey with HSC-SSP imaging. Fits are performed using both the new emulator and the default hybrid (mixture-of-Gaussians) renderer in pysersic. The best-fit models and residuals are visually indistinguishable, and the recovered parameters are consistent within uncertainties.

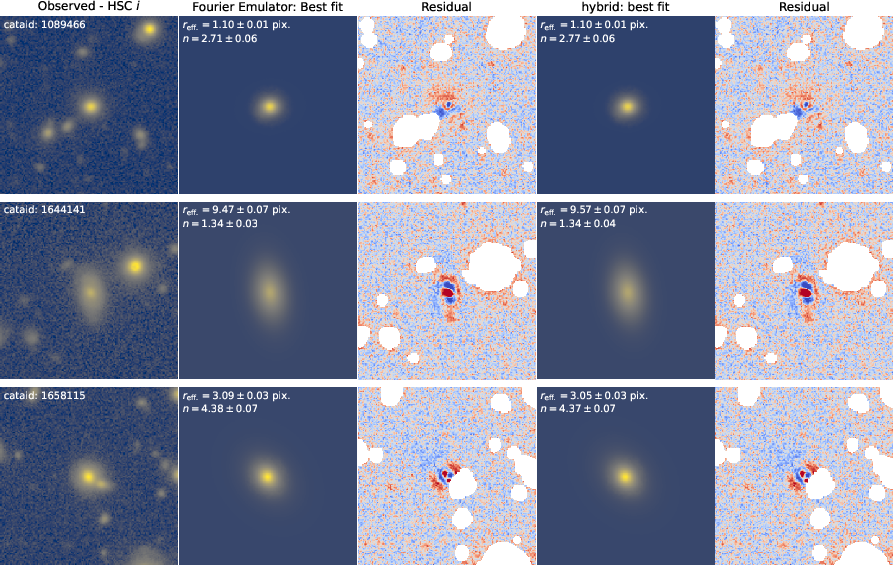
Figure 4: Profile fitting for three GAMA galaxies using both the emulator and hybrid renderers; model images and residuals are visually indistinguishable.

A quantitative comparison across the sample shows median fractional differences $<1\%$ for both $r_{\rm eff}$ and $n$, with scatter of $2.6\%$ and $4.9\%$, respectively.

Figure 5: Comparison of recovered $r_{\rm eff}$ and $n$ between emulator and hybrid renderers for 100 galaxies; differences are negligible for practical purposes.

Computational Performance

A principal advantage of the emulator is computational speed. Across both stochastic variational inference (SVI) and MCMC sampling, the emulator-based renderer achieves a $2.5\times$ reduction in inference time compared to the hybrid method. For MCMC, the median runtime drops from 64s to 23.5s per galaxy (including all overheads), and for SVI from 36.5s to 15.3s. MAP estimation is similarly accelerated.

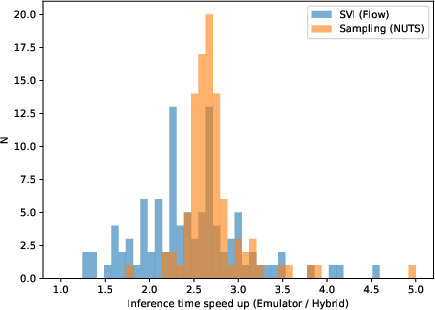
Figure 6: Inference time comparison between hybrid and emulator renderers; the emulator achieves a $2.5\times$ speedup across inference methods.

Limitations and Future Directions

The emulator is an empirical approximation, valid for $0.5 < n < 6$, which covers the majority of observed galaxies but not the full range sometimes used in profile fitting ($n$ up to 8). Symbolic regression struggled to accurately emulate the transform for $n > 6$. The emulator is also susceptible to aliasing effects inherent to Fourier-space rendering, though these are mitigated in typical use cases (central galaxies in cutouts). Future work could explore alternative loss functions more directly tied to real-space image accuracy, incorporate computational cost into the regression objective, or hybridize the emulator with real-space rendering for large-scale features.

Conclusion

This work demonstrates that symbolic regression can be used to construct a fast, accurate, and differentiable emulator for the radial Fourier transform of the Sérsic profile, enabling efficient galaxy profile fitting in Fourier space. The emulator, implemented in pysersic, achieves a $2.5\times$ speedup over standard mixture-of-Gaussians methods with negligible loss in accuracy for both synthetic and real galaxy data. This approach is well-suited for scaling morphological analysis pipelines to the data volumes of current and future extragalactic surveys, while retaining compatibility with modern gradient-based inference algorithms. Further optimization of the symbolic regression process and extension to broader parameter ranges remain promising avenues for future research.