Wave coarsening drives time crystallization in active solids (2508.20052v1)

Abstract: When metals are magnetized, emulsions phase separate, or galaxies cluster, domain walls and patterns form and irremediably coarsen over time. Such coarsening is universally driven by diffusive relaxation toward equilibrium. Here, we discover an inertial counterpart - wave coarsening - in active elastic media, where vibrations emerge and spontaneously grow in wavelength, period, and amplitude, before a globally synchronized state called a time crystal forms. We observe wave coarsening in one- and two-dimensional solids and capture its dynamical scaling. We further arrest the process by breaking momentum conservation and reveal a far-from-equilibrium nonlinear analogue to chiral topological edge modes. Our work unveils the crucial role of symmetries in the formation of time crystals and opens avenues for the control of nonlinear vibrations in active materials.

• The paper identifies wave coarsening as a novel mechanism driving time crystallization in active solids, characterized by power-law scaling.
• It employs non-reciprocal interactions in engineered 1D and 2D metamaterials to trigger self-sustained oscillations and mode coalescence.
• The study integrates experiments, simulations, and theoretical analysis to reveal robust, symmetry-protected dynamics with implications for active material design.

Wave Coarsening and Time Crystallization in Active Solids

The paper "Wave coarsening drives time crystallization in active solids" (2508.20052) presents a comprehensive experimental, theoretical, and numerical investigation of a novel route to time crystallization in active elastic media. The central result is the identification and characterization of "wave coarsening": a process in which internally powered, non-reciprocal elastic solids spontaneously generate oscillatory waves whose wavelength, period, and amplitude all grow in a self-similar, power-law fashion, culminating in a globally synchronized time-crystalline state. This mechanism is fundamentally distinct from both classical diffusive coarsening and phase-locking synchronization, and is shown to be a robust, symmetry-protected route to time crystallization in systems with momentum-conserving active stresses.

Experimental Realization of Non-Reciprocal Active Metamaterials

The authors construct two classes of active metamaterials: a two-dimensional (2D) honeycomb lattice of mechatronic hexagonal unit cells, and a one-dimensional (1D) elastic ring with non-reciprocal torsional couplings. In both systems, non-reciprocal interactions are implemented via local feedback circuits that break Maxwell-Betti reciprocity, enabling the injection of energy while conserving linear and angular momentum.

In the 2D system, each unit cell comprises three hexagons with embedded voice coil actuators and Hall sensors, orchestrated by a microcontroller to realize antisymmetric force-deformation relations. When the non-reciprocal coupling parameter $k^a$ exceeds a critical threshold, the system undergoes a Hopf bifurcation, and self-sustained oscillations emerge at the unit cell level. Upon assembling 37 such unit cells into a honeycomb lattice and minimizing substrate friction, the collective dynamics reveal the spontaneous emergence of high-wavenumber shear modes, which subsequently coarsen in wavelength and amplitude until the entire material oscillates synchronously—a haLLMark of time crystallization.

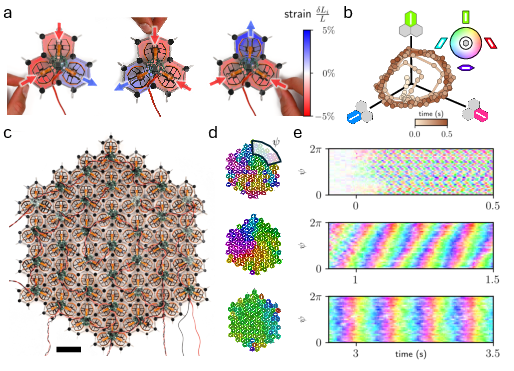
Figure 1: Wave coarsening in a non-reciprocal 2D metamaterial, showing the evolution from local oscillations to global synchronization via growth in wavelength and amplitude.

Quantitative Characterization and Dynamical Scaling

The evolution of the strain field is quantified by tracking the inverse correlation length $\xi^{-1}$ and the average elastic energy over time. Both experimental data and numerical simulations of a coarse-grained continuum model exhibit power-law scaling of the correlation length and amplitude, with exponents dependent on system dimensionality. Specifically, in 1D, $\xi^{-1} \sim t^{-1/2}$, while in 2D, a faster coarsening exponent is observed, attributed to defect dynamics.

The continuum model for the 2D system is a complex Ginzburg-Landau-type PDE for the shear strain field $\phi(x,t)$:

$$\ddot{\phi} = \nabla^2 \left[ (1-i\alpha)\phi + \dot{\phi} + |\phi|^2 \phi \right]$$

where $\alpha$ encodes the non-reciprocal activity. Linear stability analysis reveals a band of unstable wavenumbers, with the most unstable mode at $q^* = \alpha/2$. Nonlinear mode coupling leads to a progressive shift of the dominant wavenumber to lower values as the amplitude grows, resulting in self-similar coarsening dynamics.

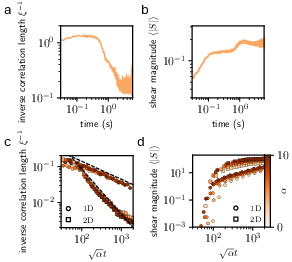
Figure 2: Power-law coarsening of the correlation length and amplitude in both experiment and simulation, confirming the dynamical scaling predictions.

Generality Across Dimensions and Nonlinearities

To demonstrate the generality of wave coarsening, the authors construct a 1D active ring of 24 torsional units with antisymmetric couplings. When driven beyond the instability threshold, high-wavenumber modes are excited and subsequently coalesce into longer-wavelength, higher-amplitude oscillations, again culminating in a time-crystalline state. The mode structure evolution is particularly transparent in 1D, with clear sequential dominance of lower-wavenumber modes and observable phase slips.

A coarse-grained beam equation with saturating nonlinearity is derived for the 1D system:

$$\ddot{h} = -\partial_x^2 \left[ \partial_x^2 h - \alpha \frac{\partial_x^3 h}{\sqrt{1+(\partial_x^3 h)^2}} + \partial_x^2 \dot{h} \right]$$

Mean-field analysis and numerical simulations yield a coarsening exponent $\xi^{-1} \sim t^{-1/4}$, in agreement with experimental observations.

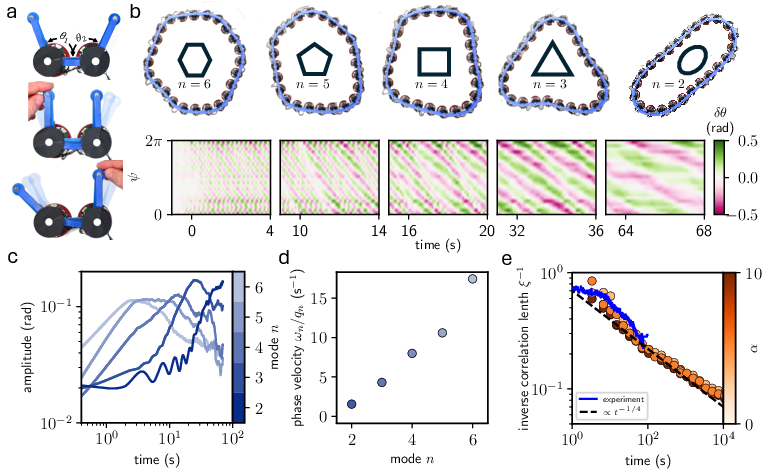
Figure 3: Wave coarsening in a 1D non-reciprocal elastic ring, showing sequential mode dominance and power-law scaling of the correlation length.

Analytical Theory: Nonlinear Mode Competition and Scaling Laws

The theoretical framework is developed by projecting the continuum equations onto Fourier modes and employing a mean-field approximation for nonlinear mode interactions. The resulting amplitude evolution equation for mode $n$ is:

$$\frac{\dot{|a_n|}}{|a_n|} = \frac{1}{2} \left( \frac{\alpha}{\sqrt{1+U(t)}} q_n^p - q_n^{2p} \right)$$

where $p=1$ for the 2D model and $p=2$ for the 1D beam, and $U(t)$ is an amplitude-dependent rescaling term. This structure leads to a feedback loop: as the amplitude grows, the effective activity decreases, shifting the most unstable mode to lower wavenumbers and slowing the coarsening rate. Power-law scaling exponents for the correlation length and amplitude are derived analytically and validated numerically.

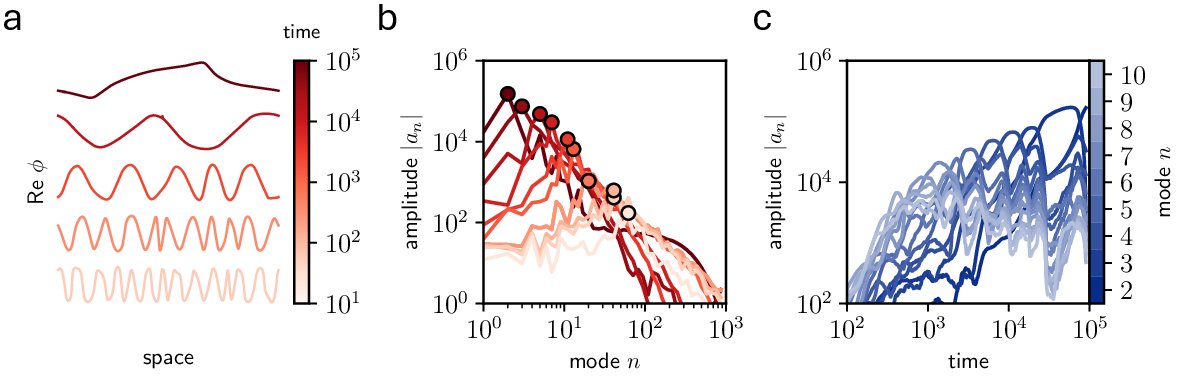
Figure 4: Numerical simulation of the $\phi$-model showing the cascade of dominant modes and the coarsening process.

Robustness: Effects of Friction and Boundaries

The robustness of wave coarsening is probed by introducing friction (breaking momentum conservation) and by varying boundary conditions. Adding friction arrests the coarsening process at a finite wavelength, as predicted by the gapped linear spectrum. Experimentally, removing PTFE lubrication halts coarsening, and the system cycles around higher-mode solutions indefinitely.

Boundary effects are explored via large-scale simulations of the 2D metamaterial on disk and annular domains. Chiral edge waves, analogous to Rayleigh waves in odd elasticity, emerge and invade the bulk, imposing spatial order and confining defects. In the presence of friction, the system supports counter-propagating edge waves with finite penetration depth, realizing a nonlinear, far-from-equilibrium analogue of topological edge states.

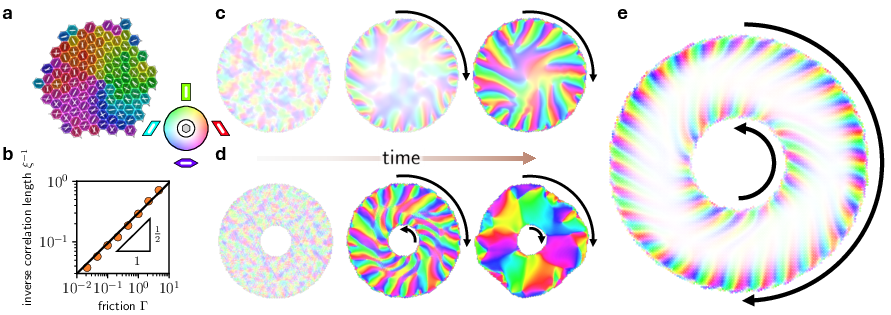
Figure 5: Arrest of wave coarsening by friction and emergence of chiral edge waves in 2D active metamaterials.

Implications and Future Directions

This work establishes wave coarsening as a generic, symmetry-protected route to time crystallization in active solids with momentum-conserving energy injection. The mechanism is fundamentally distinct from both equilibrium coarsening and phase-locking synchronization, relying on nonlinear mode competition and the absence of a global potential. The results have broad implications for the design and control of active materials, soft robotics, and optomechanical systems, particularly in contexts where non-reciprocal interactions and conservation laws are relevant.

The identification of robust, self-organized time-crystalline states in active solids opens several avenues for future research. These include the exploration of coarsening dynamics in systems with additional symmetries and Goldstone modes, the engineering of programmable shape changes and directed motion via controlled coarsening, and the realization of nonlinear topological edge states in far-from-equilibrium settings. The theoretical framework developed here provides a foundation for understanding and exploiting nonlinear wave phenomena in a wide range of active and driven systems.

Conclusion

The paper provides a detailed experimental, theoretical, and numerical paper of wave coarsening as a route to time crystallization in active solids. The identification of self-similar, power-law coarsening dynamics, the elucidation of the underlying nonlinear mode competition, and the demonstration of robustness to friction and boundary effects collectively establish wave coarsening as a paradigmatic mechanism for the emergence of time-crystalline order in active matter. The results have significant implications for the control of nonlinear vibrations and the design of active materials with programmable dynamical properties.