- The paper demonstrates that generative bandwidth is determined by the expected divergence of the score function’s vector field, highlighting symmetry-breaking phase transitions.
- The analysis integrates stochastic processes, statistical physics, and information theory to link fixed-point bifurcations with critical transitions in generative trajectories.
- The unified framework offers practical insights for refining model design, optimizing training dynamics, and enhancing generalization in diffusion models.
Integrated Theoretical Framework
This paper presents a comprehensive synthesis of the dynamic, information-theoretic, and thermodynamic properties of generative diffusion models. The central thesis is that the conditional entropy rate—termed generative bandwidth—is governed by the expected divergence of the score function’s vector field. This divergence is directly linked to the branching of generative trajectories, which are interpreted as symmetry-breaking phase transitions in the energy landscape. The analysis unifies concepts from stochastic processes, statistical physics, and information theory, providing a rigorous foundation for understanding the mechanisms underlying sample generation in diffusion models.
The paper begins by formalizing the information transfer in sequential generative modeling using conditional entropy. The analogy to the "Twenty Questions" game illustrates how information is progressively revealed or suppressed during generation. In the context of score-matching diffusion, the forward process is modeled as a stochastic differential equation, and the reverse process is guided by the score function, which acts as a non-linear filter to suppress noise incompatible with the data distribution.
The conditional entropy rate H˙(y∣xt) is derived using the Fokker-Planck equation, revealing that maximal generative bandwidth is achieved when the norm of the score function is minimized. The analysis shows that the score function’s norm decreases with the number of active data points, reflecting destructive interference in the denoising process. Peaks in the entropy rate correspond to critical transitions—noise-induced choices between possible outcomes—where symmetry breaking occurs.
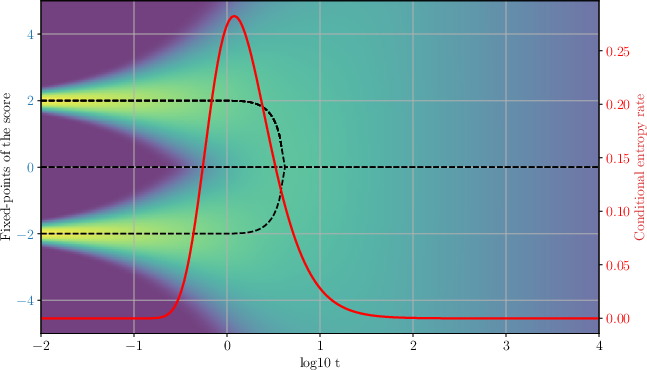
Figure 1: Conditional entropy profile (left) and paths of fixed-points (right) for a mixture of two delta distributions. The color in the background visualizes the (log)density of the process.
Statistical Physics: Fixed-Points, Bifurcations, and Phase Transitions
The connection to statistical physics is established by analyzing the fixed-points of the score function. These fixed-points, defined by ∇logpt(xt∗)=0, trace the generative decisions along denoising trajectories. Stability is determined by the Jacobian of the score, and bifurcations correspond to symmetry-breaking phase transitions. The branching of fixed-point paths is formalized as spontaneous symmetry breaking, analogous to phase transitions in mean-field models such as the Curie-Weiss magnet.
The analysis of mixtures of delta distributions demonstrates that generative bifurcations occur when the system must choose between isolated data points. The self-consistency equation for fixed-points reduces to the Curie-Weiss model, with critical transitions marked by the vanishing of the quadratic well in the energy landscape. The divergence of the score function’s vector field signals these transitions, and the sign change in the divergence corresponds to the onset of instability and branching in the generative dynamics.
Dynamics and Lyapunov Exponents
The local behavior of generative trajectories is characterized by Lyapunov exponents, which quantify the amplification of infinitesimal perturbations. After a symmetry-breaking event, negative Lyapunov exponents indicate exponential divergence of trajectories, reflecting the amplification of noise and the emergence of distinct generative outcomes.

Figure 2: Stability and instability of trajectories in different parts of a symmetry-breaking potential. Generative branching is associated with divergent trajectories.
The global perspective is obtained by studying the expected divergence of the score function over the data distribution. The data-dependent component of the divergence, Δdiv(t), encodes the separation of typical trajectories due to bifurcations. The conditional entropy rate is shown to be proportional to this expected divergence, establishing a direct link between information transfer and the geometry of the generative process.
The paper further connects entropy production to information geometry by relating the conditional entropy rate to the trace of the Fisher information matrix. The spectrum of the Fisher information matrix encodes the local tangent structure of the data manifold, and the suppression of its eigenvalues corresponds to reduced generative bandwidth. In the case of data supported on a lower-dimensional manifold, the entropy rate is proportional to the manifold’s dimensionality, and the score function acts as a linear analog filter suppressing entropy reduction in orthogonal directions.
Thermodynamic Perspective
The thermodynamic analysis reveals that conditional entropy production corresponds to the expected divergence of trajectories in the reverse process. The paradoxical increase in thermodynamic entropy during generative decisions is compensated by the forward process, ensuring compliance with the second law. This perspective clarifies the role of generative bifurcations as periods of high information transfer, where the system transitions between possible outcomes.
Implications and Future Directions
The unified framework presented in this paper has several practical and theoretical implications:
- Model Design: Understanding the connection between phase transitions and information transfer can inform the design of more efficient generative models and sampling schedules, particularly by targeting critical periods of high entropy production.
- Generalization and Memorization: The stability and topology of the score function’s fixed-points provide a rigorous tool for analyzing memorization, mode collapse, and generalization, moving beyond heuristic descriptions.
- Hierarchical Structure: The formalism suggests avenues for incorporating hierarchical and semantic structure into generative models through controlled symmetry breaking.
- Training Dynamics: Explicitly characterizing critical transitions may lead to improved training procedures that exploit periods of maximal information transfer.
Conclusion
This paper establishes a rigorous connection between the dynamics, information theory, and statistical physics of generative diffusion models. By demonstrating that generative bandwidth is governed by the expected divergence of the score function, and that generative decisions correspond to symmetry-breaking phase transitions, the analysis provides a foundation for understanding and improving the learning dynamics of modern generative AI. The framework offers new tools for model analysis and design, with potential applications in efficient sampling, generalization, and the incorporation of semantic structure. Future research may further exploit these connections to develop novel model classes and training strategies that leverage the critical dynamics of information transfer.



